看关于LBP人脸识别的论文时提到了Histogram intersection这个方法,方法最初来自The Pyramid Match Kernel:Discriminative Classification with Sets of Image Features这篇论文,用来对特征构成的直方图进行相似度匹配,下面介绍下原理。
假设图像或其他数据的特征可以构成直方图,根据直方图间距的不同可以得到多种类型的直方图:
论文里是这么设置的,假设H0(x)里每个直方图宽度为a,那么H1(x)为2a,以此类推。举个例子,假设有某计算机学院男生身高范围在160cm-200cm,H0(x)宽度可以设置为2cm,那H0(x)里会有20个直方图;类推H1(x)宽度则为4cm,H1(x)会有10个直方图。
两个数据集的相似度可以用下式来匹配:
y和z分别代表不同的数据集,比如给了两个学院男生身高,想看下这两个学院是不是同一个学院(例子不恰当,凑合着用吧^_^),用上式他们的相似度就好了。其中w代表权重,论文里将wi设置为1/(2^i),N代表每两层之间的新匹配的数目,可以通过下式计算:
上式里面的L可以通过下式计算:
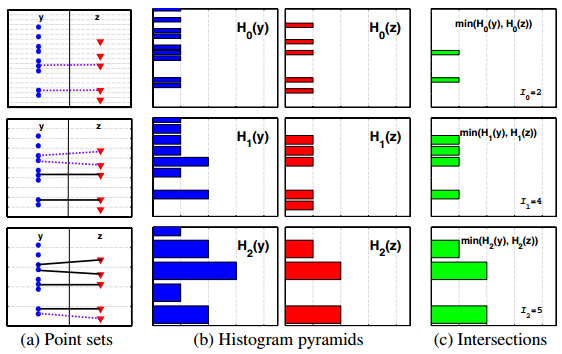
附图解释什么意思。
(a)里的y和z代表两种数据分布,三幅图代表三层金字塔,每一层里有间距相等的虚线,意思和我之前说的2cm,4cm的宽度一样。可以看到红点蓝点的位置是固定的,但是根据直方图宽度的不同可以划到不同的直方图里,如(b)所示。(c)图就是L的计算结果,是通过(b)里两种直方图取交集得来的,不过直方图的高度忽略不计,只计算交集后的数目,(c)图每个图的下方都给出了交集数目,比如x0=2,x1=4,x2=3(原图里是5,是不是错了?)。
L得到了,就算N就是通过,也就是通过Ni=Li-Li-1得到(看公式是能取负数的,比如上图里的N0=2,N1=2,N2=-1)。
由于wi之前设置为1/(2^i)了,所以
算法就是这样了,但是感觉不适合Extended LBP,因为等价模式取值不多,经不起这么多的直方图宽度变化,倒是比较适合原生的LBP方法。








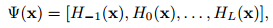
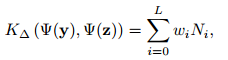
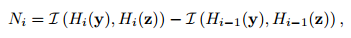
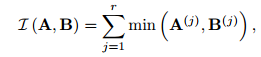
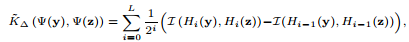

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








