说到文本相似性计算,大家首先想到的应该是使用向量空间模型VSM(Vector Space Model)。使用VSM计算相似度,先对文本进行分词,然后建立文本向量,把相似度的计算转换成某种特征向量距离的计算,比如余弦角、欧式距离、Jaccard相似系数等。这种方法存在很大一个问题:需要对文本两两进行相似度比较,无法扩展到海量文本的处理。想想像Google这种全网搜索引擎,收录了上百亿的网页,爬虫每天爬取的网页数都是百万千万级别的。为了防止重复收录网页,爬虫需要对网页进行判重处理。如果采用VSM方法,计算量是相当可观的。
这里介绍的SimHash算法很好的解决了VSM方法的缺陷,该方法最初由Google提出,用于网页去重。
在介绍SimHash前,先大概说下传统的Hash算法。我们知道,衡量一个Hash算法好坏的一个指标是随机性。也被称作简单一致散列假设:每个关键字都等可能地散列到m个槽位中的任何一个中去,并与其他的关键字已被散列到哪一个槽位中无关。说白了,就是让散列的分布尽量均匀,哪怕内容发生很小的变化,hash值也会发生很大的变化。因此,根据传统的hash值无法得知被散列内容的相似程度。
下面正式谈谈SimHash算法。它的神奇之处就在
于它的签名值除了提供原始内容是否相等的信息外,还能额外提供不相等的原始内容的差异程度的信息。SimHash的思想非常简单,如图所示:
算法描述如下:
输入为一个N维向量V,比如文本的特征向量,每个特征具有一定权重。输出是一个C位的二进制签名S。
1)初始化一个C维向量Q为0,C位的二进制签名S为0。
2)对向量V中的每一个特征,使用传统的Hash算法计算出一个C位的散列值H。对1<=i<=C,
如果H的第i位为1,则Q的第i个元素加上该特征的权重;
否则,Q的第i个元素减去该特征的权重。
3)如果Q的第i个元素大于0,则S的第i位为1;否则为0;
4)返回签名S。
对每篇文档根据SimHash算出签名后,再计算两个签名的海明距离(两个二进制异或后1的个数)即可。根据经验值,对64位的SimHash,海明距离在3以内的可以认为相似度比较高。
读到这里,你也许有一个疑惑:SimHash到底是怎样解决VSM需要两两比较的缺陷呢?请继续往下看。
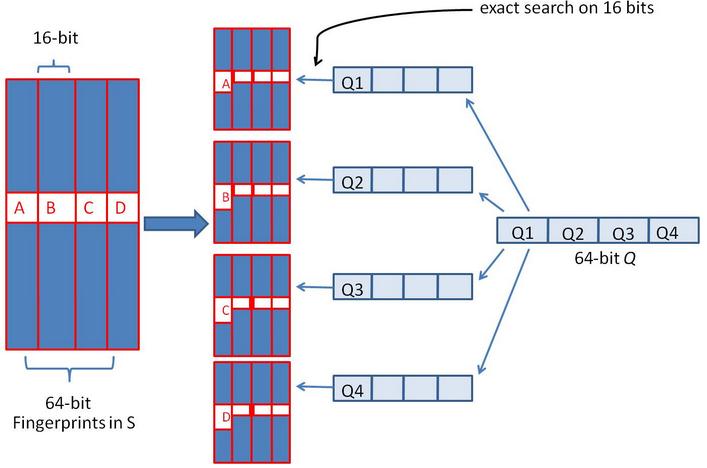
假设对64位的SimHash,我们要找海明距离在3以内的所有签名。我们可以把64位的二进制签名均分成4块,每块16位。根据鸽巢原理(也成抽屉原理,见组合数学),如果两个签名的海明距离在3以内,它们必有一块完全相同。你也许很兴奋,说的这些你都懂。但是请不要忘了,我们事先是不知道具体是哪一块完全相同,因此我们需要穷举,对,你没看错,是穷举。但是这里的穷举也就是4次而已。我们把上面分成的4块中的每一个块分别作为前16位来进行查找。什么意思呢?请看图:
通过这幅图,不知道你看明白没有,反正我还没有明白。下面让咱们一起进一步探索。
举个简单的例子,对于8位的二进制签名
01
10
00
11,咱们分别把每一块拿出来,在所有的8位二进制签名中查找前两位分别是01,10,00,11的签名。也许你要说,那不同样需要两两比较吗?对,常规意义下却是如此。但是咱们可以做索引啊!按照前两位进行索引,比如00111111和00101010放在一个簇中,10111111和10101010放在一个簇中。这下应该明白了吧。
如果库中有2^34个(大概10亿)签名,那么匹配上每个块的结果最多有2^(34-16)=262144个候选结果,四个块返回的总结果数为4* 262144(大概100万)。原本需要比较10亿次,经过索引,大概就只需要处理100万次了。由此可见,确实大大减少了计算量。
参考文献:
1.《
Similarity Estimation Techniques From Rounding Algorithms》























 171
171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








