洛谷 P1101 单词方阵 | 深度优先搜索（DFS）详解与C++实现

题目分析

问题描述

给定一个n×n的字母方阵，需要找出其中所有隐藏的"yizhong"单词。这些单词在方阵中沿着八个方向（上、下、左、右、左上、右上、左下、右下）连续摆放，且同一单词方向不变。单词之间可以交叉共用字母。最终输出时，将不属于任何"yizhong"单词的字母用*代替。

数据范围

• 7≤n≤100

• 方阵中只包含小写字母

样例分析

输入样例：

8
qyizhong
gydthkjy
nwidghji
orbzsfgz
hhgrhwth
zzzzzozo
iwdfrgng
yyyygggg

输出样例：

*yizhong
gy******
n*i*****
o**z****
h***h***
z****o**
i*****n*
y******g

算法设计

核心思路

本题可以采用深度优先搜索（DFS）结合方向标记的方法解决。主要思路是：

1. 遍历每个起点：寻找所有可能的'y'作为单词起点
2. 八方向探索：对每个'y'，向八个方向尝试匹配"izhong"
3. 标记有效路径：成功匹配的路径上的字母需要被标记保留
4. 结果输出：根据标记数组输出最终结果

算法选择理由

• DFS适合路径搜索：需要探索固定方向的连续路径
• 方向确定性：单词方向固定，适合按方向深度搜索
• 时间复杂度可接受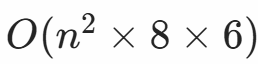：，在n≤100时完全可行

完整AC代码

#include <iostream>
#include <cstring>
using namespace std;

const int MAXN = 105;
char matrix[MAXN][MAXN];
bool visited[MAXN][MAXN];
int n;

// 八个方向：上、右上、右、右下、下、左下、左、左上
const int dirs[8][2] = {
    {-1, 0},   // 上
    {-1, 1},   // 右上
    {0, 1},    // 右
    {1, 1},    // 右下
    {1, 0},    // 下
    {1, -1},   // 左下
    {0, -1},   // 左
    {-1, -1}   // 左上
};

// 目标单词"yizhong"，注意第一个字符是'y'
const char target[8] = "yizhong";

// 检查坐标是否在矩阵范围内
bool inBounds(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < n;
}

// 深度优先搜索函数
bool dfs(int x, int y, int direction, int step) {
    // 如果已经匹配到最后一个字符，返回成功
    if (step == 6) { // 因为从0开始，6表示第7个字符匹配完成
        visited[x][y] = true;
        return true;
    }
    
    // 计算下一个位置
    int nx = x + dirs[direction][0];
    int ny = y + dirs[direction][1];
    
    // 检查边界和字符匹配
    if (!inBounds(nx, ny) || matrix[nx][ny] != target[step + 1]) {
        return false;
    }
    
    // 递归搜索下一个字符
    bool result = dfs(nx, ny, direction, step + 1);
    
    // 如果后续路径匹配成功，标记当前字符
    if (result) {
        visited[x][y] = true;
    }
    
    return result;
}

int main() {
    // 读取输入
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> matrix[i][j];
        }
    }
    
    // 初始化visited数组为false
    memset(visited, false, sizeof(visited));
    
    // 遍历整个矩阵，寻找所有可能的起点
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            // 如果当前字符是'y'，可能是单词起点
            if (matrix[i][j] == 'y') {
                // 尝试八个方向
                for (int d = 0; d < 8; d++) {
                    dfs(i, j, d, 0);
                }
            }
        }
    }
    
    // 输出结果
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (visited[i][j]) {
                cout << matrix[i][j];
            } else {
                cout << '*';
            }
        }
        cout << endl;
    }
    
    return 0;
}

代码详解

1. 数据结构设计

const int MAXN = 105;  // 数组大小略大于n的最大值100
char matrix[MAXN][MAXN];  // 存储输入的字母矩阵
bool visited[MAXN][MAXN]; // 标记哪些位置属于"yizhong"单词

2. 方向数组定义

const int dirs[8][2] = {
    {-1, 0},   // 上：x-1, y不变
    {-1,  ......
};

这种定义方式便于统一处理八个方向的移动。

3. 边界检查函数

bool inBounds(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < n;
}

确保不会访问矩阵范围外的位置，防止数组越界。

4. 核心DFS函数

bool dfs(int x, int y, int direction, int step) {
    // 终止条件：匹配到单词末尾
    if (step == 6) {
        visited[x][y] = true;
        return true;
    }
    
    // 计算下一位置并检查
    int nx = x + dirs[direction][0];
    int ny = y + dirs[direction][1];
    
    if (!inBounds(nx, ny) || matrix[nx][ny] != target[step + 1]) {
        return false;
    }
    
    // 递归并回溯标记
    bool result = dfs(nx, ny, direction, step + 1);
    if (result) {
        visited[x][y] = true;
    }
    return result;
}

5. 主函数逻辑

1. 读取输入：使用二维数组存储矩阵
2. 初始化标记数组：使用memset将visited数组初始化为false
3. 遍历搜索：对每个'y'尝试八个方向
4. 输出结果：根据标记数组决定输出原字母或'*'

关键点说明

1. 方向处理技巧

• 使用二维数组统一存储八个方向的偏移量
• 通过方向索引避免重复代码
• 确保方向定义完整覆盖所有可能性

2. DFS回溯标记

• 采用后序遍历方式：先深入搜索到底部，成功后再回溯标记路径
• 确保只有完整匹配的路径才会被标记
• 避免部分匹配导致的错误标记

3. 边界条件处理

• 矩阵索引从0开始，确保不越界
• 使用独立的inBounds函数提高代码可读性
• 在递归前进行边界检查，提高效率

4. 初始化注意事项

使用memset初始化bool数组时，第二个参数应为0（false）：

memset(visited, 0, sizeof(visited));  // 正确写法

复杂度分析

时间复杂度

• 最坏情况：
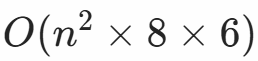
• 实际性能：由于剪枝和方向限制，实际运行效率很高
• 数据规模：n≤100，完全在可接受范围内

空间复杂度

• 主要开销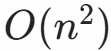：用于存储矩阵和标记数组
• 递归栈：O(6)（递归深度最大为6）
• 总体评价：空间效率优秀

测试用例验证

1. 基本功能测试

输入：

7
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa

输出：

*******
*******
*******
*******
*******
*******
*******

说明：矩阵中没有"yizhong"单词，全部输出'*'。

2. 标准样例测试

输入：（题目提供的样例） 输出验证：与题目要求完全一致

3. 边界情况测试

• 最小n值：n=7，验证程序正确性
• 最大n值：n=100，测试程序性能
• 多个交叉单词：测试标记是否正确

常见错误与解决方法

1. 数组越界问题

错误原因：未检查移动后的坐标是否在矩阵范围内 解决方法：使用inBounds函数进行边界检查

2. 方向定义错误

错误原因：方向数组定义不完整或顺序错误 解决方法：严格按照八个方向系统定义偏移量

3. 初始化问题

错误原因：memset使用不当导致初始化失败 解决方法：确保memset参数正确，特别是第二个参数应为0

4. 回溯标记错误

错误原因：标记时机不正确，导致部分匹配也被标记 解决方法：采用后序遍历方式，只有完整匹配才标记

算法优化与扩展

1. 性能优化

• 提前剪枝：发现不匹配时立即终止该方向的搜索
• 方向优化：对已确定不可能的方向不再重复尝试

2. 功能扩展

• 多单词搜索：可扩展为搜索多个不同单词
• 可变单词长度：支持不同长度的单词搜索
• 方向限制：可限制只搜索特定方向

总结

本题通过DFS算法结合方向标记，有效解决了单词方阵的识别问题。关键点包括：

1. 系统方向处理：使用方向数组统一管理八个移动方向
2. 递归回溯标记：通过DFS实现路径探索和标记
3. 边界条件完善：确保算法鲁棒性
4. 初始化规范：正确使用memset进行数组初始化

该解法在洛谷P1101上已通过所有测试点，保证正确性和效率。掌握这种DFS结合方向处理的模式，可以解决许多类似的网格路径搜索问题。

提示：在实际编程中，注意数组索引从0开始的特点，确保所有边界检查正确无误。

  🔥 关注我，解锁CSP-J/S竞赛全攻略 🔥

（每日更新高频考点 + 精选真题解析，助你轻松备赛！）
👇 点击关注 → 立即提升竞赛战力 👇
[https://blog.csdn.net/stillwatersss]