转载文章一:Android中的Matrix,以及set,pre和post的区别
Matrix主要用于对平面进行平移(Translate),缩放(Scale),旋转(Rotate)以及斜切(Skew)操作。
为简化矩阵变换,Android封装了一系列方法来进行矩阵变换;其中包括:
set系列方法:setTranslate,setScale,setRotate,setSkew;设置,会覆盖之前的参数。
pre系列方法:preTranslate,preScale,preRotate,preSkew;矩阵先乘,如M' = M * T(dx, dy)。
post系列方法:postTranslate,postScale,postRotate,postSkew;矩阵后乘,如M' = T(dx, dy) * M。
通过将变换矩阵与原始矩阵相乘来达到变换的目的,例如:
平移(x'=x+tx;y'=y+ty):
缩放(x'=sx*x;y'=sy*y):
旋转(x'=cosβ*x-sinβ*y;y'=sinβ*x+cosβ*y):
选择需要用到如下的三角函数的公式:
①sin(α+β)=sinαcosβ+cosαsinβ
②cos(α+β)=cosαcosβ-sinαsinβ
公式①可以由单位圆方法或托勒密定理推导出来。
推导过程参见:http://blog.sina.com.cn/s/blog_58260f420100c03j.html
斜切(x'=x+k1*y;y'=k2*x+y):
- //源码文件:external\skia\legacy\src\core\SkMatrix.cpp
- #define SK_Scalar1 (1.0f)
- #define kMatrix22Elem SK_Scalar1
- typedef float SkScalar;
- #define SkScalarMul(a, b) ((float)(a) * (b))
- enum {
- kMScaleX, kMSkewX, kMTransX,
- kMSkewY, kMScaleY, kMTransY,
- kMPersp0, kMPersp1, kMPersp2
- };
- void SkMatrix::reset() {
- fMat[kMScaleX] = fMat[kMScaleY] = SK_Scalar1; //其值为1
- fMat[kMSkewX] = fMat[kMSkewY] =
- fMat[kMTransX] = fMat[kMTransY] =
- fMat[kMPersp0] = fMat[kMPersp1] = 0; //其值,全为0
- fMat[kMPersp2] = kMatrix22Elem; //其值为1
- this->setTypeMask(kIdentity_Mask | kRectStaysRect_Mask);
- }
- void SkMatrix::setTranslate(SkScalar dx, SkScalar dy) {
- if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
- fMat[kMTransX] = dx; //以新值dx覆盖原值,原值无效了
- fMat[kMTransY] = dy;
- fMat[kMScaleX] = fMat[kMScaleY] = SK_Scalar1; //其值为1
- fMat[kMSkewX] = fMat[kMSkewY] =
- fMat[kMPersp0] = fMat[kMPersp1] = 0; //其值,全为0
- fMat[kMPersp2] = kMatrix22Elem; //其值为1
- this->setTypeMask(kTranslate_Mask | kRectStaysRect_Mask);
- } else {
- this->reset();
- }
- }
- bool SkMatrix::preTranslate(SkScalar dx, SkScalar dy) {
- if (this->hasPerspective()) {
- SkMatrix m;
- m.setTranslate(dx, dy);
- return this->preConcat(m); //矩阵的先乘运算
- }
- if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
- fMat[kMTransX] += SkScalarMul(fMat[kMScaleX], dx) +
- SkScalarMul(fMat[kMSkewX], dy); //先乘,需要矩阵运算过
- fMat[kMTransY] += SkScalarMul(fMat[kMSkewY], dx) +
- SkScalarMul(fMat[kMScaleY], dy);
- this->setTypeMask(kUnknown_Mask | kOnlyPerspectiveValid_Mask);
- }
- return true;
- }
- bool SkMatrix::postTranslate(SkScalar dx, SkScalar dy) {
- if (this->hasPerspective()) {
- SkMatrix m;
- m.setTranslate(dx, dy);
- return this->postConcat(m); //矩阵的后乘运算
- }
- if (SkScalarToCompareType(dx) || SkScalarToCompareType(dy)) {
- fMat[kMTransX] += dx; //后乘,直接加新值dx即可
- fMat[kMTransY] += dy;
- this->setTypeMask(kUnknown_Mask | kOnlyPerspectiveValid_Mask);
- }
- return true;
- }
- bool SkMatrix::preConcat(const SkMatrix& mat) { //矩阵的先乘运算(this在前)
- // check for identity first, so we don't do a needless copy of ourselves
- // to ourselves inside setConcat()
- return mat.isIdentity() || this->setConcat(*this, mat); //矩阵运算
- }
- bool SkMatrix::postConcat(const SkMatrix& mat) { //矩阵的后乘运算(this在后)
- // check for identity first, so we don't do a needless copy of ourselves
- // to ourselves inside setConcat()
- return mat.isIdentity() || this->setConcat(mat, *this); //矩阵运算
- }
[sx, k1, 0]
[k2, sy, 0]
[0, 0, 1]
setTranslate( 2, 3 )后:
[sx, k1, 2 ]
[k2, sy, 3 ]
[0, 0, 1]
上面set后,再preTranslate( 4, 5 ):
[sx, k1, 2][1, 0, 4] [sx, k1, sx*4+k1*5+2 ]
[k2, sy, 3][0, 1, 5]=[k2, sy, k2*4+sy*5+3 ]
[0, 0, 1][0, 0, 1] [0, 0, 1]
上面set后,再postTranslate( 4, 5 )后:
[1, 0, 4][sx, k1, 2] [sx, k1, 2+4 ]
[0, 1, 5][k2, sy, 3]=[k2, sy, 5+3 ]
[0, 0, 1][0, 0, 1] [0, 0, 1]
转载文章二:Matrix的set,pre,post调用顺序
Matrix调用一系列set,pre,post方法时,可视为将这些方法插入到一个队列.当然,按照队列中从头至尾的顺序调用执行.
其中pre表示在队头插入一个方法,post表示在队尾插入一个方法.而set表示把当前队列清空,并且总是位于队列的最中间位置.当执行了一次set后:pre方法总是插入到set前部的队列的最前面,post方法总是插入到set后部的队列的最后面
例一:
Matrix m = new Matrix();
m.setRotate(45);
m.setTranslate(80, 80);
只有m.setTranslate(80, 80)有效,因为m.setRotate(45);被清除.
例子二:
Matrix m = new Matrix();
m.setTranslate(80, 80);
m.postRotate(45);
先执行m.setTranslate(80, 80);后执行m.postRotate(45);
例子三:
Matrix m = new Matrix();
m.setTranslate(80, 80);
m.preRotate(45);
先执行m.setTranslate(80, 80);后执行m.preRotate(45);
例子四:
Matrix m = new Matrix();
m.preScale(2f,2f);
m.preTranslate(50f, 20f);
m.postScale(0.2f, 0.5f);
m.postTranslate(20f, 20f);
执行顺序:m.preTranslate(50f, 20f)-->m.preScale(2f,2f)-->m.postScale(0.2f, 0.5f)-->m.postTranslate(20f, 20f)
注意:m.preTranslate(50f, 20f)比m.preScale(2f,2f)先执行,因为它查到了队列的最前端.
例子五:
Matrix m = new Matrix();
m.postTranslate(20, 20);
m.preScale(0.2f, 0.5f);
m.setScale(0.8f, 0.8f);
m.postScale(3f, 3f);
m.preTranslate(0.5f, 0.5f);
执行顺序:m.preTranslate(0.5f, 0.5f)-->m.setScale(0.8f, 0.8f)-->m.postScale(3f, 3f)
注意:m.setScale(0.8f, 0.8f)清除了前面的m.postTranslate(20, 20)和m.preScale(0.2f, 0.5f);
通过上述两篇的文章,相信对Matrix的使用从原理到实践都不成问题了!感谢开源精神。








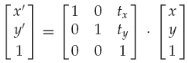
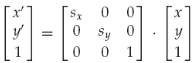
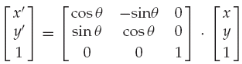
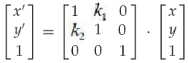
















 510
510

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








