线性回归的发展历史

简介

线性回归，可谓是机器学习领域的HelloWorld了。工作中大部分预测、监控之类的需求，都可以用线性回归来解决。

那么用了这么久，你真的了解它吗？是否是日用而不知？
线性回归是怎么来的？损失函数为何是二乘函数（最小二乘法）？如何求解最优解？

本文将对这些问题一一解答。

前世今生

线性回归并非是机器学习领域的发明，而是从其他学科领域借鉴过来。

具体地说，线性回归来自于生物学。早在19世纪，就有生物学家在研究人类的遗传时发现：人类的身高存在「回归均值」的现象。

举个栗子：姚小明的父母身高都很高（高于平均值），那么姚小明的身高不会比父母更高，而是向下趋于平均值；潘小江的父母身高都很矮（低于平均值），那么潘小江的身高不会比父母更矮，而是向上趋于平均值。

用公式表达：

孩子身高 = 人类平均身高 + 父母身高 * w

假设，人类平均身高为1.8，w为0.1，那么计算孩子的身高公式为：

孩子身高 = 1.8 + 0.1 * 父母身高

如果父母身高是2.4，孩子身高会被拽向1.8，计算得2.04；如果父母身高为1.6，孩子身高会被拉向1.8，计算得1.96。

这种现象就是「回归均值」现象，就好像有股力量拉着你，当你走向极端时，被它拉了回来。

我们今天所说的「线性回归」其实就是从「均值回归」发展来的。现在我们都知道，孩子的身高会在人类平均身高附近波动，这种波动符合正态分布，可以用最小二乘法求解w的值。可当时的人们哪知道什么是「正态分布」，又哪里知道「最小二乘法」。

曲折的最小二乘法

最小二乘法是统计学里解决线性回归问题的基础方法，那么，为什么是「最小二乘法」，而不是「最小差值法」、「最小四乘法」？

还得回到19世纪。

当时，人们经常做各种各样的实验。既然是实验，就少不了误差的干扰。就有人来研究，有什么办法来减少误差呢？

有人马上脱口而出：多次测量，取平均值！那么，为什么是平均值呢？为什么不是中位数、众数呢？

当时有个法国的科学家勒让德就想：如果每次测量都是有误差的，那么这个误差一定是在「真值」附近上下波动。那真值就应该是让这些误差波动最小的那个值，那么误差平方也会最小，而这个y就是「真值」。

举个栗子：说要测量一个物体的长度，测量了5次，测定的值分别是
$$y_1=10.3$$$$y_2=10.2$$$$y_3=9.9$$$$y_4=9.8$$$$y_5=9.8$$
假设真值是y，那么y应该是那个让5此测量误差平方和最小的值。

即求：
$$(y-y_1{)}^2+(y-y_2{)}^2+(y-y_3{)}^2+(y-y_4{)}^2+(y-y_5{)}^2$$
值最小的。

这是个关于的2次函数，很容易证明2次函数是凸函数（二阶导数>=0），所以会有最小值，且最小值在导数为0处。

求导数，另导数为0，得：
$$2(y-y_1)+2(y-y_2)+2(y-y_3)+2(y-y_4)+2(y-y_5)=0$$
求得：
$$y=(y_1+y_2+y_3+y_4+y_5)/5$$
$y$恰好是5次测量的平均值。这就回答了，为什么多次测量取平均值就能减少误差。

可是，为什么要误差平方和最小？为什么不用误差绝对值和最小？为什么不用误差4次方？这个问题勒让德也没有很好的解释，他只能说：2次方好计算。

当时有另外一个个数学家高斯有着同样的疑问。他就要一探究竟，为什么是最小2次方，而不是其他。

他用了概率的方法来解答此问题。假设真值为y，那么每次测量的误差为：$e_i=y-y_i$，误差的概率密度函数为：。
那么，5次测量的联合概率为：
$$L(y)=p(e_1)\ast p(e_2)\ast p(e_3)\ast p(e_4)\ast p(e_5)$$
即：
$$L(y)=p(y-y_1)\ast p(y-y_2)\ast p(y-y_3)\ast p(y-y_4)\ast p(y-y_5)$$
这是关于y的似然函数。

他认为，之所以观测到误差是这个结果，是因为这个结果发生的概率最大，也就是似然值最大。

最终，高斯证明：如果误差服从正态分布，那么必须要求误差的平方和最小，才能使得似然值最大，这种方法叫「极大似然估计」。

那么，测量误差是服从正态分布的吗？同时期的数据家拉普拉斯后来证明，误差还真就是服从正态分布的！

如今，我们有了结论：如果实验观测误差服从正态分布，那么可以用最小二乘法（最小化二次方之和）求解真值。

以上是根据观测值估计一个真值的情况，那么如果是估计一个函数，是否也能用最小二乘法呢？

答案是可以的。

实际上，估计函数就是估计函数的系数。

例如，有一些$(x,y)$对，发现与大致分布在一条直线上，如下图：

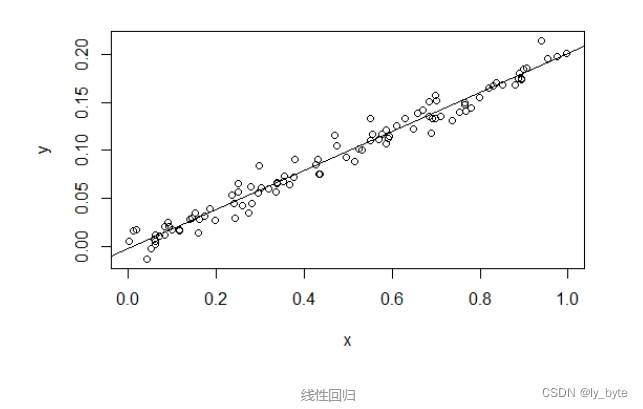
线性回归

我们可以猜测，与存在线性关系：
$$\hat{y}=w\ast x+b$$

那么对于每个，都可以用上式计算得到对应的，与的差值记作，可以看做观测值与真值的误差，如果这个误差服从「正态分布」，就可以用「最小二乘法」来估计真值了，即：
$$minL(w,b)=min\sum _{i=1}^m(w\ast x_i+b-y_i{)}^2$$
这就是我们所说的「线性回归」问题，其中，$L(w,b)$就是所说的「损失函数」。

如何求解

书接上文，「损失函数」为：
$$L(w,b)=\sum _{i=1}^m(w\ast x_i+b-y_i{)}^2$$
这是关于$(w,b)$的2次函数，分别对和求偏导数，另偏导数为0，得到方程组，解方程组即可。

很明显，方程组有两个未知数：w和b，至少需要两对不同的$(x_i,y_i)$，方程组才有解。

如果是「多元线性回归」呢？

同样可以猜测，与存在线性关系：
$$\hat{y}=w_1\ast x_1+...+w_n\ast x_n+b$$

优化目标为：
$$minL(w_1,w_2,...,w_n,b)=min\sum _{i=1}^m(\sum _{j=1}^n{w}_j\ast x_{ij}+b-y_i{)}^2$$

同样，可以求$L$对$w$各个的偏导数，另为0，解方程组得到$w_1,w_2,...,w_n,b$。

但是，这样太复杂了，我们借助矩阵、向量来解方程。

重新整理估计函数：
$$\hat{y}=w_0\ast x_0+w_1\ast x_1+...+w_n\ast x_n$$
其中，$w_0$是原来的$b$，$x_0$恒为1。

则m个观察样本为：
$${\hat{y}}^{(1)}=w_0\ast x_0^{(1)}+w_1\ast x_1^{(1)}+...+w_n\ast x_n^{(1)}$$$${\hat{y}}^{(2)}=w_0\ast x_0^{(2)}+w_1\ast x_1^{(2)}+...+w_n\ast x_n^{(2)}$$$$...$$$${\hat{y}}^{(m)}=w_0\ast x_0^{(m)}+w_1\ast x_1^{(m)}+...+w_n\ast x_n^{(m)}$$

上角标m表示第m个样本。

每个样本的误差表示为$e^{(m)}$，则有：
$$e^{(1)}=w_0\ast x_0^{(1)}+w_1\ast x_1^{(1)}+...+w_n\ast x_n^{(1)}-y^{(1)}$$$$e^{(2)}=w_0\ast x_0^{(2)}+w_1\ast x_1^{(2)}+...+w_n\ast x_n^{(2)}-y^{(2)}$$$$...$$$$e^{(m)}=w_0\ast x_0^{(m)}+w_1\ast x_1^{(m)}+...+w_n\ast x_n^{(m)}-y^{(m)}$$

用矩阵和向量表示为：
$$\left[\begin{array}{c}{e}^{(1)}\\ e^{(2)}\\ ...\\ e^{(m)}\end{array}\right]=\left[\begin{array}{ccc}{x}_0^{(1)}& x_1^{(1)}& x_n^{(1)}\\ x_0^{(2)}& x_1^{(2)}& x_n^{(2)}\\ ...& ...& ...\\ x_0^{(m)}& x_1^{(m)}& x_n^{(m)}\end{array}\right]\cdot \left[\begin{array}{c}{w}_0\\ w_1\\ ...\\ w_n\end{array}\right]-\left[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ ...\\ y^{(m)}\end{array}\right]$$
即：
$$\vec{e}=X\vec{w}-\vec{y}$$
则误差平方和为：
$${\vec{e}}^2={\vec{e}}^T\vec{e}=(X\vec{w}-\vec{y}{)}^T(X\vec{w}-\vec{y})$$
展开得到：
$${\vec{e}}^T\vec{e}={\vec{w}}^T{X}^{T}X\vec{w}-{\vec{w}}^T{X}^T\vec{y}-{\vec{y}}^{T}X\vec{w}+{\vec{y}}^T\vec{y}$$
其中，${\vec{w}}^T{X}^T\vec{y}$ 和 ${\vec{y}}^{T}X\vec{w}$的结果都是标量（实际上式中每项结果都是标量），对于标量有${\alpha }^T=\alpha$，所以 ${\vec{y}}^{T}X\vec{w}=({\vec{y}}^{T}X\vec{w}{)}^T={\vec{w}}^T{X}^T\vec{y}$，于是得到：
$${\vec{e}}^T\vec{e}={\vec{w}}^T{X}^{T}X\vec{w}-2{\vec{w}}^T{X}^T\vec{y}+{\vec{y}}^T\vec{y}$$

以上转换过程中用到了公式：
$$(AB{)}^T=B^T{A}^T$$

要求最小值，另各个偏导数为0，解方程组即可，即：
$$\frac{\partial {\vec{e}}^T\vec{e}}{\partial w_0}=0;\frac{\partial {\vec{e}}^T\vec{e}}{\partial w_1}=0;...;\frac{\partial {\vec{e}}^T\vec{e}}{\partial w_n}=0;$$
为了表示方便，我们用「梯度」来代替偏导数。梯度就是各个偏导数组成的向量：
$${\nabla }_{\vec{w}}{\vec{e}}^T\vec{e}=\frac{\partial {\vec{e}}^T\vec{e}}{\partial \vec{w}}=\left[\begin{array}{c}\frac{\partial {\vec{e}}^T\vec{e}}{\partial w_0}\\ \frac{\partial {\vec{e}}^T\vec{e}}{\partial w_1}\\ ...\\ \frac{\partial {\vec{e}}^T\vec{e}}{\partial w_n}\end{array}\right]$$

让各个偏导数为0，其实就是让梯度为0。

由于 ${\vec{x}}^{T}A\vec{x}$ 对 $\vec{x}$求导为 $(A+A^T)\vec{x}$，所以第一项${\vec{w}}^T{X}^{T}X\vec{w}$ 对 $\vec{w}$求导为$(X^{T}X+(X^{T}X{)}^T)\vec{w}$，即$2X^{T}X\vec{w}$ ；对于第二项 $2{\vec{w}}^T{X}^T\vec{y}$对 $\vec{w}$求导为$2X^T\vec{y}$ ；

合并整理得：
$${\nabla }_{\vec{w}}{\vec{e}}^T\vec{e}=\frac{\partial {\vec{e}}^T\vec{e}}{\partial \vec{w}}=2X^{T}X\vec{w}-2X^T\vec{y}$$

另梯度为0，得到：
$$2X^{T}X\vec{w}-2X^T\vec{y}=0$$

计算$\vec{w}$为：
$$\vec{w}=(X^{T}X{)}^{-1}{X}^T\vec{y}$$

这样，就可以直接用解方程的方式来计算$\vec{w}$了。

梯度下降求解

理论上只要$X^{T}X$可逆，就能用解方程的方式求解$\vec{w}$了，但如果$X^{T}X$是个非常大的矩阵，甚至大到无法把一个矩阵放入内存，求逆矩阵就没有那么容易了，这时就需要使用「梯度下降法」来求近似解了。

大体思想是，任意选择一个 $\vec{w}$ 的初始值，计算此时的梯度（前边已经提到了梯度，即偏导数组成的向量），使 $\vec{w}$沿着梯度方向前进一小步$\alpha$ ，重复以上步骤，如果梯度小于某个临界值 $e$，则终止。

参考：
[http://www.52nlp.cn/正态分布的前世今生四]
[最小二乘法的历史回顾与现状]

| 文章出处：https://www.jianshu.com/p/74096ef5a5fb