算法快学笔记（十四）：图的最小生成树算法

最新推荐文章于 2023-04-19 20:52:30 发布

铁猴

最新推荐文章于 2023-04-19 20:52:30 发布

阅读量2.6k

点赞数 8

分类专栏：趣学算法与数据结构文章标签：图算法最小生成树 Prim Kruskal Python

本文链接：https://blog.csdn.net/eric_sunah/article/details/102724378

版权

趣学算法与数据结构专栏收录该内容

26 篇文章 25 订阅

订阅专栏

1. 介绍

最小生成树的应用场景很广，例如电信公司需要将9个村庄进行网络连接，村庄间的距离都不相同，怎么连接才能达到成本最小了？村庄结构图如下：
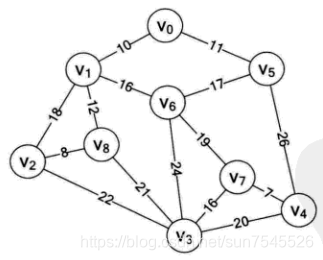
在这里插入图片描述

V0-V10分别表示村庄，节点间的权重代表距离，连接所有节点的总距离最小，就可以让成本更低。

定义：把构造连通整个图的最小代价生成树称为最小生成树。

2. 相关算法

普利姆与克鲁斯卡尔算法都是贪心算法

2.1 普利姆(Prim)算法

2.1.1 原理

普里姆算法（Prim算法）：该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

算法的基本步骤如下：

输入：一个加权连通图，其中顶点集合为V，边集合为E；
初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
重复下列操作，直到Vnew = V：

在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
将v加入集合Vnew中，将<u, v>边加入集合Enew中；

输出：使用集合Vnew和Enew来描述所得到的最小生成树。

算法实例推理步骤如下：
在这里插入图片描述

2.1.2 代码实现

基于邻接矩阵存储结构用Python实现的代码如下：

# -*- coding:utf-8 -*-
# @Author：sunaihua
"""
普里姆算法（Prim算法）:最小生成树算法
本实现基于邻接矩阵存储结构
"""
MAX_VALUE = 65536

# 图结构的矩阵存储
graph = [
    [0, 10, MAX_VALUE, MAX_VALUE, MAX_VALUE, 11, MAX_VALUE, MAX_VALUE, MAX_VALUE],
    [10, 0, 18, MAX_VALUE, MAX_VALUE, MAX_VALUE, 16, MAX_VALUE, 12],
    [MAX_VALUE, MAX_VALUE, 0, 22, MAX_VALUE, MAX_VALUE, MAX_VALUE, MAX_VALUE, 8],
    [MAX_VALUE, MAX_VALUE, 22, 0, 20, MAX_VALUE, MAX_VALUE, 16, 21],
    [MAX_VALUE, MAX_VALUE, MAX_VALUE, 20, 0, 26, MAX_VALUE, 7, MAX_VALUE],
    [11, MAX_VALUE, MAX_VALUE, MAX_VALUE, 26, 0, 17, MAX_VALUE, MAX_VALUE],
    [MAX_VALUE, 16, MAX_VALUE, MAX_VALUE, MAX_VALUE, 17, 0, 19, MAX_VALUE],
    [MAX_VALUE, MAX_VALUE, MAX_VALUE, 16, 7, MAX_VALUE, 19, 0, MAX_VALUE],
    [MAX_VALUE, 12, 8, 21, MAX_VALUE, MAX_VALUE, MAX_VALUE, MAX_VALUE, 0],
]

start_node = 0  # 0节点为初始节点

new_v_array = [] #最小生成树的vertex数组
edge_value_array = [] #最小生成树的权值数组
new_e_array = [] #最小生成树的edge数组


def prim():
    v_number = len(graph)
    latest_edge_target = -1
    new_v_array.append(start_node)
    while True:
        if len(new_v_array) < v_number:
            smallest_value = MAX_VALUE
            for n_index in new_v_array:
                cur_net = graph[n_index]
                for index, value in enumerate(cur_net): # 选出new_v_array中所有边的最小值
                    if index not in new_v_array:
                        if (value != 0) and (value <= smallest_value):
                            smallest_value = value
                            latest_edge_target = index
                            latest_edge_src = n_index
                    else:
                        continue
                    print(new_v_array, n_index, index, value, smallest_value, latest_edge_target)
            if latest_edge_target not in new_v_array:
                print("merge:", latest_edge_src, latest_edge_target, smallest_value)
                new_e_array.append([latest_edge_src, latest_edge_target])
                new_v_array.append(latest_edge_target)
                edge_value_array.append(smallest_value)
        else:
            break

    print("V seq:", new_v_array)
    print("E seq:", new_e_array)
    print("sum value:", sum(edge_value_array))


if __name__ == '__main__':
    prim()

2.1.3 结果

程序的部分输出结果为：

('V seq:', [0, 1, 5, 8, 2, 6, 7, 4, 3])
('E seq:', [[0, 1], [0, 5], [1, 8], [8, 2], [1, 6], [6, 7], [7, 4], [7, 3]])
('sum value:', 99)

连接文章开头部分的最小值为99.

关于时间复杂度问题：

如果记顶点数v，边数e，则采用邻接矩阵的算法复杂度为：

O = V^2

采用邻接表的时间复杂度为:O(elog2v)

2.2 克鲁斯卡尔(Kruskal)算法

2.2.1 原理

Kruskal算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。

算法简单描述如下：

1).记Graph中有v个顶点，e个边

2).新建图Graph_new，Graph_new中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从小到大排序

4).循环：从权值最小的边开始遍历每条边直至图Graph中所有的节点都在同一个连通分量中，如果这条边连接的两个节点于图Graph_new中不在同一个连通分量中则添加这条边到图Graph_new中

推理过程如下：
图例描述：

首先第一步，我们有一张图Graph，有若干点和边

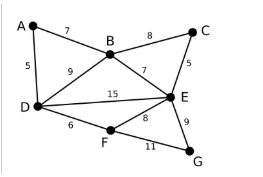
在这里插入图片描述

将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了下图

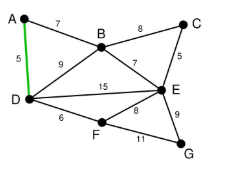
在这里插入图片描述

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

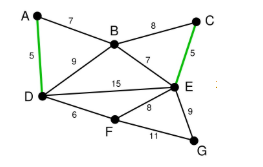
在这里插入图片描述

依次类推我们找到了6,7,7，即DF，AB，BE。

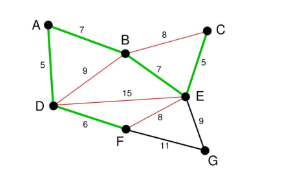
在这里插入图片描述

下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。
最后就剩下EG和FG了。当然我们选择了EG。最后成功的图如下所示：
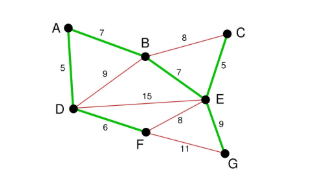
在这里插入图片描述

2.1.2 实现

# -*- coding:utf-8 -*-
# @Author：sunaihua

"""
Kruskal:最小生成树算法
本实现基于邻接矩阵存储结构
"""
import copy

MAX_VALUE = 65536

# 图结构的矩阵存储
graph = [
    [0, 10, MAX_VALUE, MAX_VALUE, MAX_VALUE, 11, MAX_VALUE, MAX_VALUE, MAX_VALUE],
    [10, 0, 18, MAX_VALUE, MAX_VALUE, MAX_VALUE, 16, MAX_VALUE, 12],
    [MAX_VALUE, MAX_VALUE, 0, 22, MAX_VALUE, MAX_VALUE, MAX_VALUE, MAX_VALUE, 8],
    [MAX_VALUE, MAX_VALUE, 22, 0, 20, MAX_VALUE, MAX_VALUE, 16, 21],
    [MAX_VALUE, MAX_VALUE, MAX_VALUE, 20, 0, 26, MAX_VALUE, 7, MAX_VALUE],
    [11, MAX_VALUE, MAX_VALUE, MAX_VALUE, 26, 0, 17, MAX_VALUE, MAX_VALUE],
    [MAX_VALUE, 16, MAX_VALUE, MAX_VALUE, MAX_VALUE, 17, 0, 19, MAX_VALUE],
    [MAX_VALUE, MAX_VALUE, MAX_VALUE, 16, 7, MAX_VALUE, 19, 0, MAX_VALUE],
    [MAX_VALUE, 12, 8, 21, MAX_VALUE, MAX_VALUE, MAX_VALUE, MAX_VALUE, 0],
]

new_v_array = []  # 最小生成树的vertex数组
edge_value_array = []  # 最小生成树的权值数组
new_e_array = []  # 最小生成树的edge数组


class Vertex:
    def __init__(self, distance, x, y):
        self.distance = distance
        self.x = x
        self.y = y

    def __eq__(self, other):
        if isinstance(other, self.__class__):
            return self.x == other.y and self.y == other.x
        else:
            return False

    def __hash__(self):
        m1 = min(self.x, self.y)
        m2 = max(self.x, self.y)
        return hash(("[%s,%s,%s]" % (m1, m2, self.distance)))

    def __repr__(self):
        return "[%s,%s,%s]" % (self.x, self.y, self.distance)


def find(parent, f):
    while parent[f] > 0:
        f = parent[f]
    return f


def kruskal():
    edge_with_distance = set()
    for i, v_net in enumerate(graph):
        for j, k in enumerate(v_net):
            if i != j and k != MAX_VALUE:
                edge_with_distance.add(Vertex(k, i, j))
    # 根据distance排序，并将利用set特性将相同的节点去掉
    sorted_graph = sorted(edge_with_distance, key=lambda x: x.distance, reverse=False)
    parent = [0 for _ in range(len(graph))]
    for ve in sorted_graph:
        if len(new_v_array) == (len(graph)):
            break
        n = find(parent, ve.x)
        m = find(parent, ve.y)
        # 如果n==m,则表明存在循环节点。
        if n != m:
            parent[n] = m
            print("parent2:", parent)
            new_v_array.append(ve)
            new_e_array.append((ve.x, ve.y))
            edge_value_array.append(ve.distance)

    print("V seq:", new_v_array)
    print("E seq:", new_e_array)
    print("sum value:", sum(edge_value_array))


if __name__ == '__main__':
    kruskal()

2.1.3 结果

输出结果与Prim结果相同

3. 总结

Prim算法以顶点为起点，逐步寻找顶点上最小权值的边来构建最小生成树，就像参加世博会，先从第一个入口进，然后寻找所在场馆周边最感兴趣的馆，然后再用相同的办法查看下一个。。。。。

Kruskal算法是基于权值最小的边来构建生成树，该思路参加世博园就是先去最想参观的馆，再参观次想参观的馆，最终参观完所有馆。

关于算法效率，Kruskal针对边来展开，边少时效率非常高，是和用于稀疏图。Prim适用于边比较多的场景。

铁猴

关注

8
点赞
踩
40

收藏

觉得还不错? 一键收藏
2
评论
算法快学笔记（十四）：图的最小生成树算法

1. 介绍最小生成树的应用场景很广，例如电信公司需要将9个村庄进行网络连接，村庄间的距离都不相同，怎么连接才能达到成本最小了？村庄结构图如下：V0-V10分别表示村庄，节点间的权重代表距离，连接所有节点的总距离最小，就可以让成本更低。定义：把构造连通整个图的最小代价生成树称为最小生成树。2. 相关算法普利姆与克鲁斯卡尔算法都是贪心算法2.1 普利姆(Prim)算法2.1.1 原理...
复制链接

扫一扫