【从线性回归到BP神经网络】第一部分：协方差与相关系数

本文主要参考文献如下：
1、吴恩达CS229课程讲义。
2、（美）S.Chatterjee等，《例解回归分析》（第2章），机械工业出版社。
3、周志华. 《机器学习》3.2.清华大学出版社。
4、（美）P.Harrington，《机器学习实战》人民邮电出版社。

  由于数据处理经常需要计算样本的统计特性，这里我们首先对此进行讨论。

1、样本均值

  对于随机变量$X$，其均值$m_X=\mathrm{E}(x)$，方差为${\sigma }_X^2=\mathrm{E}[(x-m_X{)}^2]$。设有$X$的样本 { x 1 , x 2 , … , x n } \{x_1,x_2,\ldots,x_n\} {x1​,x2​,…,xn​}，则样本均值为
$${\hat{m}}_X=\frac{1}{n}\sum _{i=1}^n{x}_i.\text{\hspace{1em}(1)}$$

可以证明，${\hat{m}}_x$是均值$m_x$的无偏估计，即$\mathrm{E}[{\hat{m}}_X]=m_X$，证明如下：
$$\begin{array}{rl}\mathrm{E}[{\hat{m}}_x]& =\mathrm{E}\left[\frac{1}{n}\sum _{i=1}^n{x}_i\right]\\ & =\frac{1}{n}\sum _{i=1}^n\mathrm{E}\left[x_i\right]\\ & =\frac{1}{n}\sum _{i=1}^n{m}_X=m_X.\end{array}$$

2、样本方差

  对于随机变量$X$，其均值$m_X=\mathrm{E}(x)$，方差为${\sigma }_X^2=\mathrm{E}[(x-m_X{)}^2]$，样本方差为
$${\hat{\sigma }}_X^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-{\hat{m}}_X{)}^2.\text{\hspace{1em}(2)}$$

  我们来看为何上式中求样本方差时，为何对$n$项求和，却除以$n-1$呢？
  这主要是因为我们希望${\hat{\sigma }}_X^2$是${\sigma }_X^2$的无偏估计，如果我们除以$n$，会遇到下面情况：
$$\begin{array}{rl}\mathrm{E}\left[{\hat{\sigma }}_X^2\right]& =\mathrm{E}\left[\frac{1}{n}\sum _{i=1}^n(x_i-{\hat{m}}_X{)}^2\right]\\ & =\frac{1}{n}\mathrm{E}\left[\sum _{i=1}^n(x_i-{\hat{m}}_X{)}^2\right]\\ & =\frac{1}{n}\mathrm{E}\left[\sum _{i=1}^n(x_i^2+{\hat{m}}_X^2-2x_i{\hat{m}}_X)\right]\\ & =\mathrm{E}\left[\frac{1}{n}\sum _{i=1}^n{x}_i^2-{\hat{m}}_X^2\right]\\ & =\frac{1}{n}\sum _{i=1}^n\mathrm{E}\left[x_i^2\right]-\mathrm{E}\left[{\hat{m}}_X^2\right]\\ & =\mathrm{E}\left[x^2\right]-\mathrm{E}\left[{\hat{m}}_X^2\right]\\ & =(\mathrm{E}\left[x^2\right]-m_X^2)-(\mathrm{E}\left[{\hat{m}}_X^2\right]-m_X^2)\\ & ={\sigma }_X^2-\mathrm{v}\mathrm{a}\mathrm{r}[{\hat{m}}_X^2]\end{array}$$由于$$\begin{array}{rl}\mathrm{v}\mathrm{a}\mathrm{r}[{\hat{m}}_X^2]& =\mathrm{v}\mathrm{a}\mathrm{r}\left[\frac{1}{n}\sum _{i=1}^n{x}_i\right]\\ & =\frac{1}{n^2}\sum _{i=1}^n\mathrm{v}\mathrm{a}\mathrm{r}\left[x_i\right]\\ & =\frac{{\sigma }_X^2}{n}\end{array}$$因此
$$\begin{array}{r}\mathrm{E}\left[{\hat{\sigma }}_X^2\right]=\frac{n-1}{n}{\sigma }_X^2\end{array}$$显然不是${\sigma }_X^2$的无偏估计。因此，我们将该估计进行修正，可以得到
$$\begin{array}{rl}\mathrm{E}\left[{\hat{\sigma }}_X^2\right]& =\mathrm{E}\left[\frac{1}{n-1}\sum _{i=1}^n(x_i-{\hat{m}}_X{)}^2\right]\\ & =\frac{1}{n-1}\mathrm{E}\left[\sum _{i=1}^n(x_i-{\hat{m}}_X{)}^2\right]\\ & =\frac{1}{n-1}\mathrm{E}\left[\sum _{i=1}^n(x_i^2+{\hat{m}}_X^2-2x_i{\hat{m}}_X)\right]\\ & =\frac{1}{n-1}\mathrm{E}\left[\sum _{i=1}^n{x}_i^2-n\cdot {\hat{m}}_X^2\right]\\ & =\mathrm{E}\left[\frac{1}{n}\sum _{i=1}^n{x}_i^2-{\hat{m}}_X^2\right]\\ & =\frac{n}{n-1}\left(\mathrm{E}\left[x^2\right]-\mathrm{E}\left[{\hat{m}}_X^2\right]\right)\\ & ={\sigma }_X^2\end{array}$$为无偏估计。

3、协方差

  下面我们来定义两个随机变量$X$和$Y$的样本的协方差，这里假设$X$的样本为 { x 1 , x 2 , … , x n } \{x_1,x_2,\ldots,x_n\} {x1​,x2​,…,xn​}，$Y$的样本为 { y 1 , y 2 , … , y n } \{y_1,y_2,\ldots,y_n\} {y1​,y2​,…,yn​}，则有
$$\mathrm{c}\mathrm{o}\mathrm{v}(X,Y)=\frac{{\sum }_{i=1}^n(y_i-{\hat{m}}_Y)(x_i-{\hat{m}}_X)}{n-1}.\text{\hspace{1em}(3)}$$

4、相关系数

  进一步，可以对两个随机变量进行标准化处理，得到$X$和$Y$的相关系数为
$$\begin{array}{rl}\mathrm{c}\mathrm{o}\mathrm{r}(Y,X)& =\frac{1}{n-1}\sum _{i=1}^n(\frac{y_i-{\hat{m}}_Y}{{\hat{\sigma }}_Y})(\frac{x_i-{\hat{m}}_X}{{\hat{\sigma }}_X})\\ & =\frac{1}{n-1}\sum _{i=1}^n\frac{(y_i-{\hat{m}}_Y)(x_i-{\hat{m}}_X)}{{\hat{\sigma }}_Y{\hat{\sigma }}_X}\\ & =\frac{{\sum }_{i=1}^n(y_i-{\hat{m}}_Y)(x_i-{\hat{m}}_X)}{\sqrt{\sum (x_i-{\hat{m}}_X{)}^2\sum (x_i-{\hat{m}}_X{)}^2}}\end{array}\text{\hspace{1em}(4)}$$

注意相关系数的如下性质：

1. $$\mathrm{c}\mathrm{o}\mathrm{r}(Y,X)=\mathrm{c}\mathrm{o}\mathrm{r}(X,Y)$$
2. $$-1\le \mathrm{c}\mathrm{o}\mathrm{r}(Y,X)\le 1$$
3. 相关系数只能刻画变量间线性关系的强弱。
4. 相关系数会受到数据中一个或者几个离群值的显著影响。

5、 示例：数据集的相关系数计算

  下面我们看个例子。我们计算下表中的四个数据集，分别计算相关系数，并画出散点图。

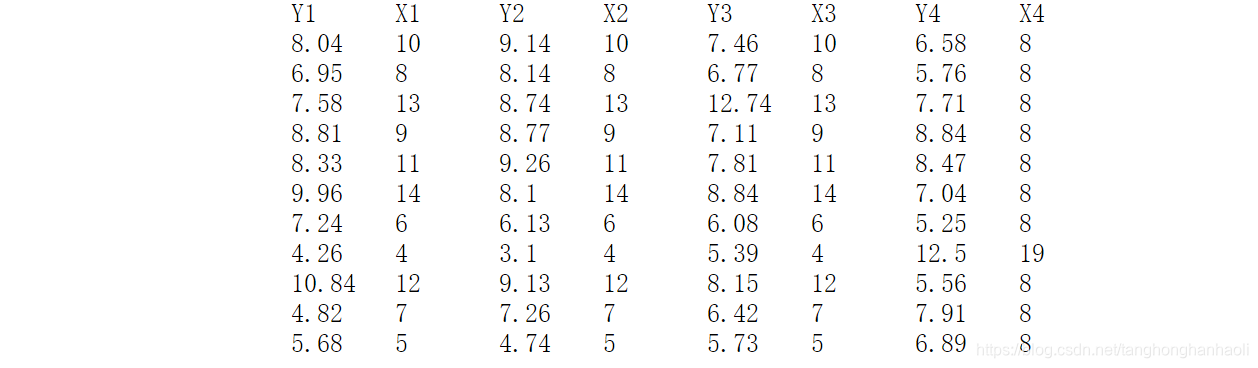
Matlab代码如下：

A=load('Data_Chap2_Anscombe.txt')
Cor_12=corrcoef(A(:,1),A(:,2))
Cor_34=corrcoef(A(:,3),A(:,4))
Cor_56=corrcoef(A(:,5),A(:,6))
Cor_78=corrcoef(A(:,7),A(:,8))
subplot(2,2,1)
scatter(A(:,2),A(:,1))
subplot(2,2,2)
scatter(A(:,4),A(:,3))
subplot(2,2,3)
scatter(A(:,6),A(:,5))
subplot(2,2,4)
scatter(A(:,8),A(:,7))

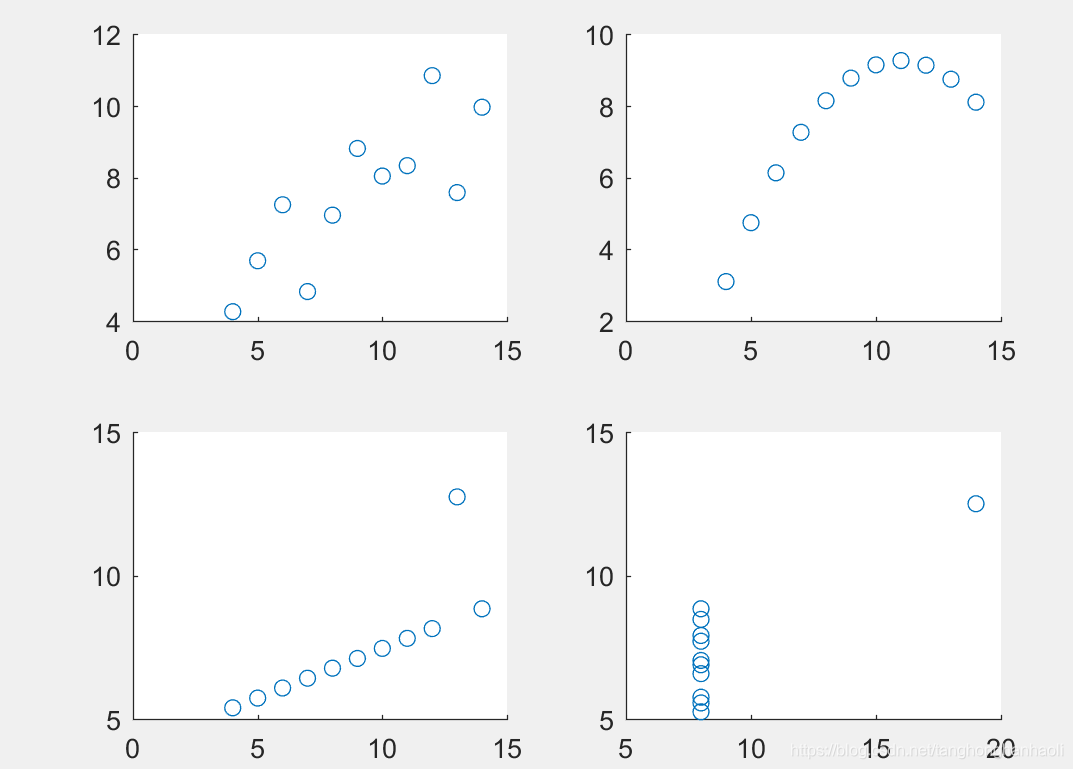
得到相关系数为

Cor_12 =
    1.0000    0.8164
    0.8164    1.0000

Cor_34 =
    1.0000    0.8162
    0.8162    1.0000

Cor_56 =
    1.0000    0.8163
    0.8163    1.0000

Cor_78 =
    1.0000    0.8165
    0.8165    1.0000

  显然，尽管相关系数基本相等，但从下图散点图中可以看出，四组数据$Y$与$X$的函数关系差别很大。因此在计算相关系数之前，考察散点图是非常有帮助的。