🌟个人主页:第七序章
🌈专栏系列:C++


目录
❄️前言:
前面我们学习了unordered_set和unordered_map,在
unordered_set和unordered_map中,其底层是用哈希表实现的,今天我们就来学习一下哈希表的实现,了解其底层原理!
☀️一、什么是哈希表
哈希(Hash)又称为散列,是一种组织数据的映射方式;
哈希表(Hash Table)是一种高效的数据结构,它通过哈希函数将键(Key)映射到数组索引,从而实现快速的插入、删除和查找等操作。
哈希表的效率为O(1),比起线性结构(数组、链表)等效率要高。
底层结构是哈希表的unordered_set和unordered_map 相比于底层结构是红黑树的set和map,哈希表的效率要略快一点,但差距并不大。
🌙1. 哈希函数
哈希的本质就是通过
哈希函数将键值Key映射到数组索引;那哈希函数有哪些呢?
⭐直接定址法
当我们数据相对比较集中的时候,直接定址法就是非常的好用。
什么意思呢?
简单来说,假设现在的数据范围是
[0 , 99],那我们开辟100个空间的数组,此时每一个key值就是其对应的下标。
其实这种方法之前就是用过:387. 字符串中的第一个唯一字符
对于上面只一道题,我们做法就是开辟一个26大小的字符数组,然后遍历数组统计每个字符出现的次数;最后遍历字符串,看哪一个字符最先只出现了一次。
class Solution {
public:
int firstUniqChar(string s) {
int arr[26] = {0};
for(auto& ch:s)
{
arr[ch - 'a']++;
}
for(int i = 0;i<s.size();i++)
{
if(arr[s[i]-'a'] == 1)
return i;
}
return -1;
}
};
常见的哈希函数还用很多:
⭐除留余数法/除法散列法
- 除留余数法,顾名思义:假设我们哈希表的大小为
M,那通过Key除以M的余数作为映射位置的下标。也就是哈希函数:Hash(Key) = Key % M。- 当我们使用
除留余数法时,尽量避免M为某一些值(2的幂、10的幂等)。为什么呢?- 如果我们的
M等于2的x次幂,那进行取模%操作,本质上就是保留Key的2进制后x位,这样很容易就引起冲突;(10的x次幂同理,当M为这些数时,很容易就引起冲突,冲突多了哈希表的效率就降低了。- 这里也不是说非得要这样,就比如java中的HashMap就是采用2的整数次幂作为哈希表的大小;但是它并不是单纯的取模,假设M是2^16,本质上是取16位:key' = key>>16,然后将key和key'异或的结果作为哈希值。(简单来说,就是2进制下的前多少位和后多少位进行异或运算);这样相对而言异或运算要比取模更好的。
这里,只能说像理论那样说,尽量不要取2的整数次幂、10的整数次幂;但是呢,在实践中我们要灵活应用,而不是死记这些。
⭐乘法散列法(了解)
乘法散列法,它对哈希表大小M就没有啥要求了;
这个方法的思路就是先将关键字K乘上常数A(0 < A < 1),并取出来乘积的小数部分,再用M乘上小数部分,向下取整
h(key) = floor(M*((A*key)%1.0)) ,其中floor表示向下取整,A∈(0,1);
这里重要的是A值该如何去取,Knuth认为A取值 “黄金分割点” 较好。
⭐全域散列法(了解)
全域散列法的核心思想是通过引入随机化的散列函数,来避免不同数据的散列值碰撞(即两个不同的数据映射到同一个位置)。这种方法通过以下步骤实现:
- 随机化函数:全域散列法通过随机选取一些参数(例如随机种子)来生成多个散列函数。这些函数作用于输入数据时,会产生不同的散列值,增加了散列结果的随机性。
- 选择最佳函数:全域散列法会根据某些标准(例如冲突次数、效率等)选择一个最优的散列函数。这样可以确保散列结果尽量分布均匀,减少碰撞的概率。
- 全局范围:与传统的局部散列方法不同,全域散列法考虑到全局的数据集和表格,使用全局的散列函数设计,使得不同的数据之间有较大的映射差异,从而减少碰撞的机会。
- 这里需要注意:每一次初始化哈希时,就会随机选取全域散列函数组中的一个散列函数;在后序增删查改操作都固定使用这一个散列函数。(否则,如果每一次都是随机选一个哈希函数,插入选择一个、查找选择一个,就会导致找不到对应的
key了)
⭐其他方法
这里像乘法散列法、全域散列了解一下就好了;
当然还有其他的方法,《殷人昆数据结构:用面向对象方法与C++语言描述(第二版)》和《数据结构[C语言].严蔚敏_吴伟民》这些教材上海给出了平方取中法、折叠法、随机数法、数学分析等,这些就更加适用于一些特定的场景,有兴趣的可以看一下。
🌙2. 冲突和冲突解决
无论我们设计再好的
哈希函数,冲突还是不可避免的,那我们遇到冲突时该如何去解决呢?
⭐开放定址法
开放地址法是另一种常用的冲突解决方法,其基本思想是,当发生冲突时,探测哈希表中其他位置,直到找到一个空桶为止。常见的探测策略有线性探测、二次探测和双重哈希。
⭐线性探测
- 在发生冲突时,依次检查当前位置的下一个位置(按照顺序)直到找到空位置。
- 简单来说,遇到冲突时
hc(key,i) = hashi = (hash0 + i )%M,其中hash0指的是第一次映射的位置; - 遇到冲突时会一直进行查找,直到找到空位置。
⭐二次探测
- 当发生冲突时,采用平方级的步长探测。例如,探测位置为
h(k) + 1^2, h(k) + 2^2, h(k) + 3^2。 - 简单来说,遇到冲突时,
hc(key,i) = hashi = (hash0 +/- i^2 )%M - 这里当
hc(key,i) = hashi = (hash0 - i^2 )%M,当hashi<0时,需要进行hashi+M。
⭐双重哈希
- 简单来说,当第一个哈希函数计算的值发生冲突,就压使用第二个
哈希函数计算出一个和key相关的偏移量,这样不断往后演策,直到下一个没有存储数据位置。 - 使用第二个哈希函数来计算探测步长,每次发生冲突时,都通过第二个哈希函数来决定探测位置。
- 当第一个哈希函数遇到冲突了,要使用第二个哈希函数来决定探测位置。
这里主要还是
线性探测,其他的了解一下。
🌙3. 负载因子
假设现在
哈希表已经存储了N个值,哈希表的大小为M,那负载因子就等于N/M负载因子越大,哈希表中数据个数
N就约接近哈希表的大小M,冲突的概率就越大,空间利用率就越高;负载因子越小,哈希冲突概率就越低,空间复用率就越低。
🌙4. 关键字key转化成整型问题
我们将关键字映射到数组中位置,一般都是整数好做计算,不是整数也是那个通过强制类型转换变成整型的数据
在
uordered_set第二个模版参数和unordered_map的第三个模版参数Hash = hash<K>就是将数据类型K转化成整型。
☀️二、开放定址法实现
这里简单实现一下开放定址法,就哈希函数采用除留余数法、选取线性探测来解决哈希冲突。
⭐哈希表结构
先来看一下我们要实现的哈希表的结构:
enum STATE
{
EXIST,
DELETE,
EMPTY
};
template<class K, class V>
struct HashData
{
pair<K, V> _kv;
STATE _state = EMPTY;
};
template<class K, class T>
class HashTable
{
private:
vector<Hashdata<K, V>> _table;
size_t = _n = 0;
};
这里来看一下
哈希表的结构:
- 首先就是
HashTable,其中包含了一个vector数组来存储数据,和size_t类型的_n表示当前的数据个数。HashData表示哈希表中vector存储的数据类型,其中包含pair<K,V>表示存储的数据,_state表示当前位置此时的状态(有EXIST存在、DELETE删除和EMPTY空)。
⭐insert
对于
insert插入,我们了解hash表的插入规则
- 首先要找到
key值映射到数组的位置 使用除留余数法来进行映射(使用hash0来记录)- 然后就是解决冲突问题,(如果当前位置已经有值了,那就要解决,这里采用线性探测来解决哈希冲突)
还有一个最重要的点,就是扩容问题,如果我们的负载因子
N/M大于等于0.7,那就要进行扩容操作:对于扩容操作,这里我们可以定义一个新的vector<HashData>然后遍历原表,依次将每一个数据重新映射到新的数组中;(这样我们就要重新写一次,映射和冲突解决的逻辑。我们还可以这样来写,创建一个新的表(新表的大小是扩容后的大小),然后进行复用insert操作即可。
逻辑如上,现在来看代码:
bool insert(const pair<K, V>& kv)
{
//扩容
if ((double)_n / (double)_table.size() >= 0.7)
{
size_t newsize = __stl_next_prime(_table.size() + 1);
HashTable<K, V> newHT;
newHT._table.resize(newsize);
//遍历原哈希表
for (int i = 0; i < _table.size(); i++)
{
if (_table[i]._state == EXIST)
newHT.insert(_table[i]._kv);
}
//交换新旧表中的_table
_table.swap(newHT._tale);
}
//插入逻辑
size_t hash0 = kv.first % _table.size();
size_t hashi = hash0;
int i = 1;
while (_table[hashi] == EXIST)
{
hashi = (hash0 + i) % _table.size();
i++;
}
_table[hashi]._kv = kv;
_table[hashi]._state = EXIST;
_n++;
return true;
}
这里我们实现的
insert遇到重复的key它是可以继续插入的;这里没有解决这个问题在我们实现
find以后,进行一下判断即可解决。
⭐find
对于
find,其逻辑和我们插入数据相似首先找到映射的位置hash0,然后定义hashi和i开始查找,如果遇到冲突就重新映射hashi = (hash0 +i) %_table.size()。
如果找到当前位置存在_table[hashi]._state == EXIST并且值等于key (_table[hashi]._kv.first == key)。就返回当前pair<K.V>的指针。
如果遍历结束也没有找到,那就返回
nullptr。
在
find查找这里,我们才意识到STATE的作用:就是如果我们某一个位置的数据已经删除了,那我们是将它的状态置为DELETE而不是EMPTY,这样我们在查找的过程中,结束的条件是当前位置的状态等于EMPTY这样就是删除了中间一个值,我们也会查找到其后面的值。
HashData<K,V>* find(const K& key)
{
size_t hash0 = key % _table.size();
size_t hashi = hash0;
int i = 1;
while (_table[hashi] != EMPTY)
{
if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
{
return &_table[hashi];
}
hashi = (hash0 + i) % _table.size();
i++;
}
return nullptr;
}
⭐erase
对于
erase我们可以自己再次去实现查找,当然可以直接复用find,这里就直接复用了。
bool erase(const K& key)
{
HashData<K, V>* ret = find(key);
if (ret != nullptr || ret->_state == EXIST)
{
ret->_state = DELETE;
return true;
}
else
return false;
}
⭐key不能直接转化成整型问题
我们需要给
HashTable增加一个仿函数,但是我们在使用unordered_set和unordered_map时,当key是整型时,我们没有传递这个仿函数啊,这是因为库里面给了缺省参数(这个缺省参数就是直接取K强制转换成整型的结果)。那
key是string时,我们也没有传啊,难道string还能强转成整型不成?这是因为
string相对是非常常用的,库里面就对模版进行了特化,让我们每次使用string时不用去参这个参数。那如果
key不能够转化成整形,且库里面也没有支持,那我们就要自己去实现一个仿函数,显示传递过去。
这里简单实现一下,将string转成整型的方法有很多,这里就简单实现一种。
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct HashFunc<string>
{
public:
size_t operator()(const string& str)
{
size_t ret = 1;
int i = 1;
for (auto& ch : str)
{
ret += ch * i;
i++;
}
return ret;
}
};
有了这个仿函数,我们之前进行取模操作的地方都要套用一层hash。
☀️三、链地址法及其实现
链地址法,与开发地址法不同的地方就在于处理冲突的方法,我们开发地址法解决的大体思路就是,重新找到一个新的位置;
而链地址不同,它每一个位置不单单是存储一个数据了,而是一个单链表的头指针,当遇到冲突时,它不会去找一个新的位置,而是继续将数据放到链表中。
这样我们哈希表每一个位置存放的都是一个单链表,向挂起来的桶一样,所以也称其为哈希桶。
这我们将
{19,30,5,36,13,20,21,12,24,96}映射到M = 11的表中:
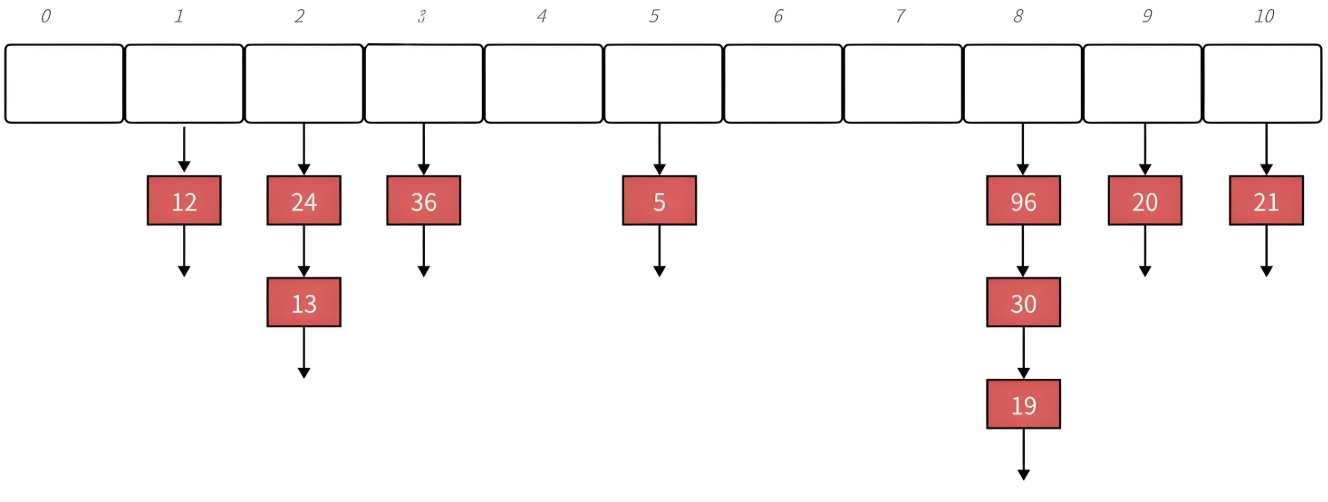
先来看一下链地址法中哈希表的结构
⭐哈希表结构
template<class K,class V>
struct HashNode
{
HashNode(const pair<K, V>& kv)
:_kv(kv)
, _next(nullptr)
{}
pair<K, V> _kv;
HashNode<K, V>* _next;
};
template<class K,class V>
class HashTable
{
typedef HashNode<K, V> Node;
public:
HashTable()
{
_table.resize(__stl_next_prime(0));
}
private:
vector<Node*> _table;
size_t _n = 0;
};
这里
HashTable里还是存储的一个vector数组和_n表示当前数据个数。
HashNode中存储的是pair<K,V>数据和_next下一个节点的指针。
⭐扩容操作
链地址法与上述
开发地址法实现起来可以是非常相似;但是扩容的逻辑大有差别在
开发地址法中,我们扩容是创建一个新的表,遍历旧表,将数据重新映射插入到新表当中;但是我们这里存储的数据是一个个节点的指针,如果依旧按照上述操作,将数据重新插入到新表中就也些浪费了。
加上现在表中有
500个数据,如果向上述那样重新创建500个节点并释放旧的,那很浪费啊。
所以我们不能像开发定址法那样,而是将旧表中数据节点移动到新表当中去。
⭐inerst
bool insert(const pair<K, V>& kv)
{
//扩容
if ((double)_n / (double)_table.size() >= 1)
{
size_t newsize = __stl_next_prime(_table.size() + 1);
vector<Node*> newtable;
newtable.resize(newsize);
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
size_t hash0 = cur->_kv.first % newsize;
cur->_next = newtable[hash0];
newtable[hash0] = cur;
cur = cur->_next;
}
}
_table.swap(newtable);
}
//插入
size_t hash0 = kv.first % _table.size();
//头插到当前位置
Node* newnode = new Node(kv);
newnode->_next = _table[hash0];
_table[hash0] = newnode;
_n++;
return true;
}
⭐find
find操作相对就简单很多了
Node* find(const K& key)
{
size_t hashi = key % _table.size();
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
return cur;
cur = cur->_next;
}
return false;
}
⭐erase
删除操作不能上面一样复用
find,因为我们的数据是一个个的节点,我们删除一个节点还要考虑它前一个节点的指针指向。所以这里自己查找,删除,并修改前驱指针的指向。
bool erase(const K& key)
{
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
Node* prve = nullptr;
while (cur)
{
if (key == cur->_kv.first)
{
if (prve == nullptr)
{
_table[i] = cur->_next;
}
else
{
prve->_next = cur->_next;
}
delete cur;
--_n;
return true;
}
prve = cur;
cur = cur->_next;
}
}
}
⭐析构函数
编译器会自动调用
vector的析构函数,但是链地址法内存放的是指针,需要我们自己去释放指针指向的空间,所以我们要自己写析构函数。
~HashTable()
{
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
对于
key转化成整型,与开发定址法中一样,这里就不叙述了。
⭐代码总览:
现在将Hash添加进去,这样可以实现自定义类型转整型:
修改后的代码如下:
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct HashFunc<string>
{
size_t operator()(const string& str)
{
size_t ret = 1;
int i = 1;
for (auto& ch : str)
{
ret += ch * i;
i++;
}
return ret;
}
};
template<class K,class V>
struct HashNode
{
HashNode(const pair<K, V>& kv)
:_kv(kv)
, _next(nullptr)
{}
pair<K, V> _kv;
HashNode<K, V>* _next;
};
template<class K,class V, class Hash = HashFunc<K>>
class HashTable
{
typedef HashNode<K, V> Node;
public:
HashTable()
{
_table.resize(__stl_next_prime(0));
}
bool insert(const pair<K, V>& kv)
{
if (find(kv.first) != nullptr)
return false;
Hash hs;
//扩容
if ((double)_n / (double)_table.size() >= 1)
{
size_t newsize = __stl_next_prime(_table.size() + 1);
vector<Node*> newtable;
newtable.resize(newsize);
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
size_t hash0 = hs(cur->_kv.first) % newsize;
//size_t hash0 = cur->_kv.first % newsize;
cur->_next = newtable[hash0];
newtable[hash0] = cur;
cur = cur->_next;
}
}
_table.swap(newtable);
}
//插入
size_t hash0 = hs(kv.first) % _table.size();
//size_t hash0 = kv.first % _table.size();
//头插到当前位置
Node* newnode = new Node(kv);
newnode->_next = _table[hash0];
_table[hash0] = newnode;
_n++;
return true;
}
Node* find(const K& key)
{
Hash hs;
size_t hashi = hs(key) % _table.size();
//size_t hashi = key % _table.size();
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
return cur;
cur = cur->_next;
}
return false;
}
bool erase(const K& key)
{
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
Node* prve = nullptr;
while (cur)
{
if (key == cur->_kv.first)
{
if (prve == nullptr)
{
_table[i] = cur->_next;
}
else
{
prve->_next = cur->_next;
}
delete cur;
--_n;
return true;
}
prve = cur;
cur = cur->_next;
}
}
}
~HashTable()
{
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
private:
vector<Node*> _table;
size_t _n = 0;
};
☀️四、本文小结
| 类别 | 核心内容 |
|---|---|
| 哈希表基础 | 1. 定义:通过哈希函数将键(Key)映射到数组索引,实现快速增删查改(效率 O (1))2. 优势:比红黑树结构的 set/map 略快3. 核心问题:哈希函数设计、冲突解决、负载因子控制、关键字转整型 |
| 哈希函数 | 1. 直接定址法:键值直接作为索引(适用于数据集中场景,如 26 个字母统计)2. 除留余数法:Hash (Key) = Key % M(M 避免 2 的幂 / 10 的幂,减少冲突)3. 乘法散列法:h (key) = floor (M*((A*key)%1.0)),A 取黄金分割点(了解)4. 全域散列法:随机选取哈希函数减少冲突(了解)5. 其他:平方取中法、折叠法等(特定场景) |
| 冲突解决 | 1. 开放定址法:- 线性探测:hashi = (hash0 + i) % M- 二次探测:hashi = (hash0 +/- i²) % M- 双重哈希:冲突时用第二个哈希函数计算步长2. 链地址法(哈希桶):冲突数据存入同一位置的单链表 |
| 负载因子 | 定义:N/M(N 为数据个数,M 为表大小)影响:值越大冲突概率越高、空间利用率越高;值越小则相反 |
| 关键字转整型 | 1. 库实现:unordered_set/unordered_map 通过模板参数 Hash = hash<K>处理2. 自定义:通过仿函数实现(如 string 转整型:累加字符 × 权重) |
| 开放定址法实现 | 1. 结构:vector 存储 HashData(含键值对 + 状态:EXIST/DELETE/EMPTY)2. 插入:哈希映射→线性探测找空位→负载因子≥0.7 时扩容(重新映射旧数据)3. 查找:根据状态遍历探测位置4. 删除:标记状态为 DELETE(不直接置空,避免影响查找) |
| 链地址法实现 | 1. 结构:vector 存储单链表头指针(HashNode 含键值对 + next 指针)2. 插入:头插至哈希映射的链表→负载因子≥1 时扩容(迁移旧节点,不重建)3. 查找:遍历对应链表4. 删除:找到节点后调整前驱指针,释放内存5. 析构:手动释放所有链表节点 |
🌻共勉:
以上就是本篇博客的所有内容,如果你觉得这篇博客对你有帮助的话,可以点赞收藏关注支持一波~~🥝