参考
.PageRank算法--从原理到实现
零. PageRank算法简介
PageRank算法,即网页排名算法,由Google创始人Larry Page在斯坦福上学的时候提出来的。该算法用于对网页进行排名,排名高的网页表示该网页被访问的概率高。
该算法的主要思想有两点:
a. 如果多个网页指向某个网页A,则网页A的排名较高。
b. 如果排名高A的网页指向某个网页B,则网页B的排名也较高,即网页B的排名受指向其的网页的排名的影响。
一、PageRank算法原理
1. 简单的PageRank算法
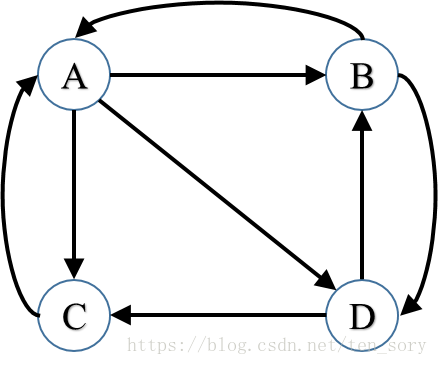
如图是一个4个网页之间的链接情况:
假设网页X的排名用PR(X)表示,则A的排名为PR(A),由图可知,网页B和C指向了网页A,那么网页A的排名可以表示为:
网页C只指向了A,不指向其他网页,然而网页B不仅指向了A,还指向了D,因此上面的公式更合理地修改为:
意思是,B的PageRank值被分给了A和D,而C的PageRank值全都给了A。
2. 考虑没有出边(outlink)的网页
有的网页,没有指向其他网页,如下图中的C网页。








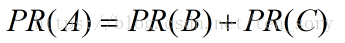
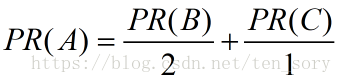
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








