Codeforces 1178 F2 Long Colorful Strip —— 记忆化区间DP

最新推荐文章于 2021-10-19 19:55:36 发布

原创最新推荐文章于 2021-10-19 19:55:36 发布 · 348 阅读

1 ·

CC 4.0 BY-SA版权

想法同时被 2 个专栏收录

495 篇文章

订阅专栏

202 篇文章

订阅专栏

本文深入探讨一种复杂的区间动态规划问题，旨在计算在给定条形和颜色约束下，如何有效填充颜色以达到特定分布的目标。通过合并连续相同颜色区间，采用递归方式枚举分割点，最终实现高效求解方案数量。

This way

题意：

给你一个长度为m的条，现在有n种颜色，从1开始填色，你可以将一段连续的相同颜色的区间填成这个颜色，最后要使得这个条的颜色分布如下，问你有多少种填法。

题解：

比较难的区间DP。
首先将连续的相同值区间合并，因为我们知道如果a[i]=a[i-1]，那么在这个位置就一定不会有分割的情况。
dp一个区间的时候找到这个区间的最小值，因为它是基础，在做完它之后就不会在做到这个数了。
那么这个最小数的区间建立之后，将整个区间划分成了3个，
就像这样：
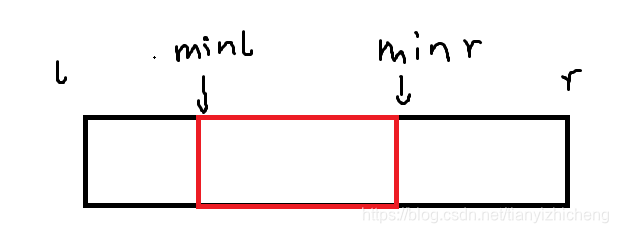
在这里插入图片描述
我们dp出前面的区间的情况数*后面区间的情况数*中间的情况数就是答案。
也就是枚举分割点在l-minl，r-minr的情况。
对于中间的情况，递归下去做即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e6+5,M=1e3+5;
const ll mod=998244353;
int a[N];
ll dp[M][M];
vector<int>vec[M];
ll dfs(int l,int r)
{
    if(l>r)
        return 1;
    if(~dp[l][r])
        return dp[l][r];
    int mi=a[l];
    for(int i=l;i<=r;i++)
        mi=min(mi,a[i]);
    int le=vec[mi][0],rig=vec[mi][(int)(vec[mi].size()-1)];
    ll a_l=0,a_r=0,ans=0;
    for(int i=l;i<=le;i++)
        a_l=(a_l+dfs(l,i-1)*dfs(i,le-1))%mod;
    for(int i=rig;i<=r;i++)
        a_r=(a_r+dfs(rig+1,i)*dfs(i+1,r))%mod;
    ans=a_l*a_r%mod;
    for(int i=0;i<vec[mi].size()-1;i++)
        ans=ans*dfs(vec[mi][i]+1,vec[mi][i+1]-1)%mod;
    dp[l][r]=ans;
    return ans;
}
int main()
{
    memset(dp,-1,sizeof(dp));
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
        scanf("%d",&a[i]);
    int all=unique(a+1,a+1+m)-a-1;
    for(int i=1;i<=all;i++)
        vec[a[i]].push_back(i);
    if(all>2*n)
        return 0*printf("0\n");
    printf("%lld\n",dfs(1,all));
    return 0;
}