QR分解

原创于 2017-01-14 10:18:46 发布 · 5.4k 阅读

9 ·

CC 4.0 BY-SA版权

Math 同时被 2 个专栏收录

15 篇文章

订阅专栏

矩阵与数值分析

15 篇文章

订阅专栏

本文介绍了QR分解法的基本概念及其在解决线性最小二乘法问题中的应用，并详细讲解了使用Householder变换进行QR分解的具体步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、简介

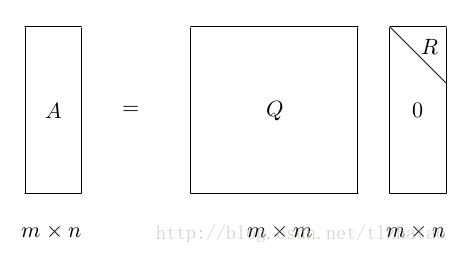
QR分解法是三种将矩阵分解的方式之一。这种方式，把矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR 分解经常用来解线性最小二乘法问题。QR 分解也是特定特征值算法即QR算法的基础。同时，QR分解后的矩阵与原矩阵的条件数保持一致。

QR分解的实际计算有很多方法，例如Givens旋转、Householder变换，以及Gram-Schmidt正交化等等。每一种方法都有其优点和不足。
详解

二、实现

通过Householder变换实现QR分解。

# -*- coding: utf-8 -*-
"""
Created on Thu Dec 15 13:46:30 2016

    QR分解

@author: Administrator
"""

from numpy import *
from numpy.linalg import norm

def householder(x,y):
    m = x.shape[0]
    n = y.shape[0]
    if m != n:
        return
    y = sign(x[0]) * norm(x) * y / norm(y)
    u = x - y
    I = eye(n,dtype=float)
    H = I - 2 * outer(u,u) / inner(u,u)
    return H

def qr(A):
    m,n = A.shape
    R = A.copy()
    Q = zeros((n,n),dtype=float)
    for i in range(0,n):
        Q[i,i] = 1
    for i in range(0,n-1):
        x = R[i:n,i].getA1()
        y = zeros(n-i,dtype=float)
        y[0] = 1
        temp_H = householder(x,y)
        H = eye(n,n,dtype=float)
        H[i:n,i:n] = temp_H[0:n-i,0:n-i]
        Q = dot(Q,H)
        R = dot(H,R)  
    return Q,R

if __name__ == '__main__':
    A = array([[1,2,3,4,0],[-1,3,sqrt(2),3,0],[-2,2,e,pi,0],[-sqrt(10),2,-3,7,0],[0,2,7,5/2,0]],dtype=float)
    A = matrix(A,dtype=float)
    Q,R = qr(A)
    print R