函数、反函数

张宇说：函数用铅直渐近线、反函数用水平渐近线判断是否为单值函数

一、函数

1. 定义

设x与y是两个变量，D是一个给定的数集。若对于每一个x∈D，按照一定的法则f，都有一个确定的值y与之对应，则称y为x的函数，记作y=f(x)，称x为自变量，y为因变量，称数集D为此函数的定义域。即当自变量确定时，函数值必须唯一确定。

比如y²=x，一个x对应两个y，所以不是函数

2. 函数成立的两个基本条件（重要）

• 一对一的映射关系 成为函数的条件
• 定义域

2.1. 定义域

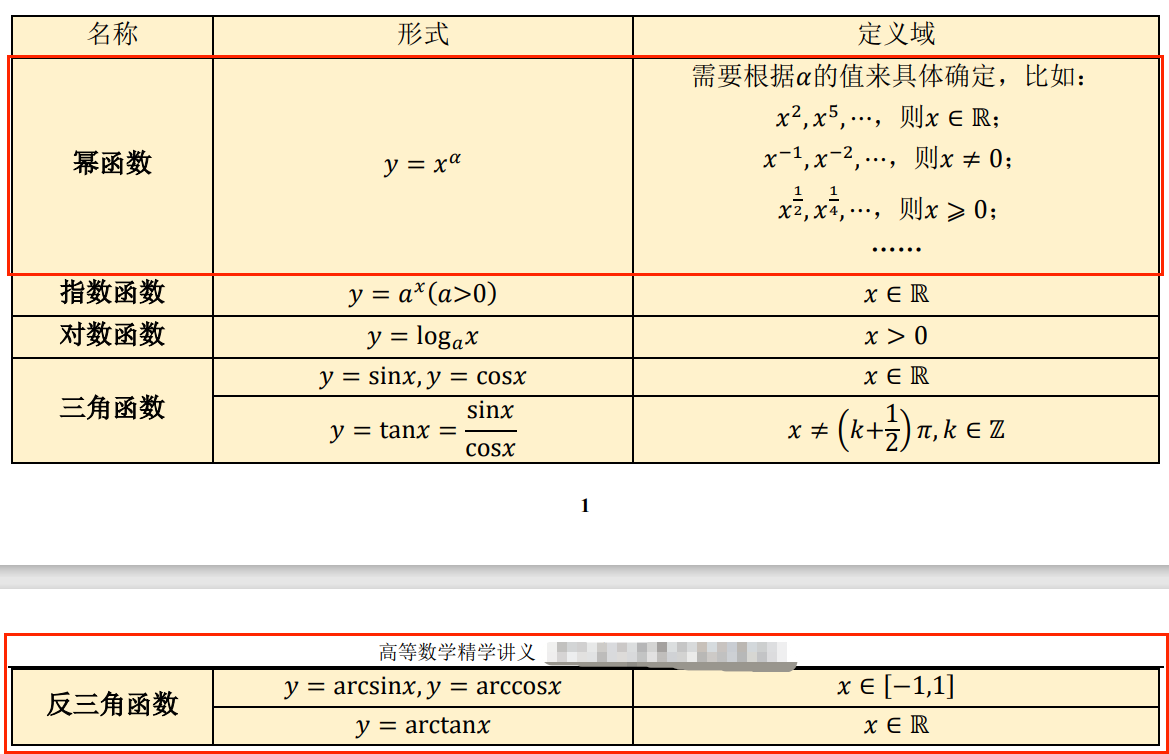
3. 函数的四种特性

有界性、单调性、奇偶性、周期性

3.1. 有界性（常考证明）

有界：有上界+有下界

设f(x)的定义域为D，数集I⊂D 。如果存在某个正数M，使对于任一x∈I，有|f(x)|≤M&#