分类算法属性选择度量--信息增益、增益率、Gini指标

属性选择度量就是分裂规则，用来确定分裂属性和分裂子集

---

信息增益

信息增益：某属性的信息增益值越大，这个属性作为一棵树的根节点就能使这棵树更简洁，降低树的高度。衡量给定属性划分训练样本的能力。计算信息增益的公式需要用到“熵”（Entropy）。

熵：衡量任意样本集的纯度，熵越小，样本纯度越高。以二分类为例，

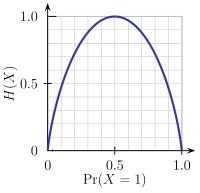
H（X）表示熵，横坐标表示类别A在这两个类{A,B}中的百分比，越接近0.5，表示两个类对抗越明显。值越接近0，表示某个类占的比例越大或越小，也就是样本纯度越高。