接上篇:
BRDF理论及shader实现(上)
Specular BRDF
对于specular分量来说, f m f_m fm是一个遵循菲涅尔反射定律的镜面BRDF项,此时的 f m f_m fm满足([3]和[21]有详细的推导):
f m ( l , v , m ) = F ( v , m ) δ ω m ( h , m ) 4 ( l ⋅ h ) 2 f_m({\bf{l}},{\bf{v}},{\bf{m}}) = F({\bf{v}},{\bf{m}})\frac{\delta_{\omega_m}({\bf{h}}, {\bf{m}})}{4({\bf{l}}\cdot{\bf{h}})^2} fm(l,v,m)=F(v,m)4(l⋅h)2δωm(h,m)
h {\bf{h}} h表示half vector,是 v {\bf{v}} v和 l {\bf{l}} l的平均;这里分母上第一次出现了 4 4 4,这也是后面specular BRDF公式的分母上的 4 4 4的来源。 δ ω m ( s , o ) \delta_{\omega_m}({\bf{s}}, {\bf{o}}) δωm(s,o)记为:
∫ Ω g ( o ) δ ω o ( s , o ) d ω o = { g ( s ) , if s ∈ Ω 0 , otherwise \int_\Omega g({\bf{o}})\delta_{\omega_o}({\bf{s}}, {\bf{o}})d\omega_o = \begin{cases} g({\bf{s}}), & \text {if $s\in\Omega$} \\ 0, & \text{otherwise} \end{cases} ∫Ωg(o)δωo(s,o)dωo={g(s),0,if s∈Ωotherwise
此时, f r f_r fr可以化简为为:
f r ( l , v ) = D ( h , α ) G ( v , l , α ) F ( v , h , F 0 ) 4 ( n ⋅ v ) ( n ⋅ l ) f_r({\bf{l}},{\bf{v}}) = \frac{D({\bf{h}},\alpha)G({\bf{v}},{\bf{l}},\alpha)F({\bf{v}},{\bf{h}},F_0)}{4({\bf{n}}\cdot{\bf{v}})({\bf{n}}\cdot{\bf{l}})} fr(l,v)=4(n⋅v)(n⋅l)D(h,α)G(v,l,α)F(v,h,F0)
其中, α \alpha α取决于我们前面提到的粗糙度roughness,具体为
α = r o u g h n e s s 2 \alpha = roughness^2 α=roughness2
可以理解为 α \alpha α是对粗糙度roughness的一个映射, α \alpha α将多次被用到。
菲涅尔项及 F 0 F_0 F0会在后面详细介绍,这里暂时略过。
shader实现:
// #define saturate(x) clamp(x, 0, 1)
// N = normal;
// V = normalize(camPos - WorldPos);
// L = normalize(LightPos - WorldPos));
// H = normalize(V + L);
// NdotV = saturate(dot(N, V));
// NdotL = saturate(dot(N, L));
// NdotH = saturate(dot(N, H));
// LdotH = saturate(dot(L, H));
// VdotH = saturate(dot(V, H));
vec3 SpecularBRDF(float NdotV, float NdotL, float NdotH, float LdotH, float VdotH, vec3 F0, float roughness) {
float r = roughness * roughness;
float D = Distribution(NdotH, r);
float V = Geometry(NdotV, NdotL, r);
vec3 F = Fresnel(VdotH, F0);
return D * V * F / (4 * NdotV * NdotL);
}
注意,这里的NdotL,NdotV等都是clamp到0到1的。
接下来具体看 f r f_r fr中每个分量的可能形式都有哪些。
法向分布函数 D
这一部分介绍3个法向分布函数的公式,以及一个推广。
Beckmann
来源[5], D B e c k m a n n D_{Beckmann} DBeckmann假设微表面的法向分布是以 n {\bf{n}} n为均值的高斯分布,也即 h {\bf{h}} h与 n {\bf{n}} n越接近,反射的光线越多, D B e c k m a n n D_{Beckmann} DBeckmann越大。再结合 D B e c k m a n n D_{Beckmann} DBeckmann的积分约束,求得:
D B e c k m a n n ( h , α ) = χ + ( n , h ) π α 2 ( n ⋅ h ) 4 e ( n ⋅ h ) 2 − 1 α 2 ( n ⋅ h ) 2 D_{Beckmann}({\bf{h}}, \alpha) = \frac{\chi^+({\bf{n}},{\bf{h}})}{\pi\alpha^2({\bf{n}}\cdot{\bf{h}})^4}e^{\frac{({\bf{n}}\cdot{\bf{h}})^2-1}{\alpha^2({\bf{n}}\cdot{\bf{h}})^2}} DBeckmann(h,α)=πα2(n⋅h)4χ+(n,h)eα2(n⋅h)2(n⋅h)2−1
这个公式有一个很致命的缺陷,那就是当roughness接近于1的时候, D B e c k m a n n D_{Beckmann} DBeckmann在 n ⋅ h ∈ [ 0 , 1 ] {\bf{n}}\cdot{\bf{h}}\in[0,1] n⋅h∈[0,1]区间内,不是单调递增的。表现在渲染上,就是在高光最强的中心点会产生一个暗斑。
shader实现:
float DistributionBeckmann(float NdotH, float r) {
float NdotH2 = NdotH * NdotH;
float r2 = r * r;
float r2NdotH2 = r2 * NdotH2;
return exp((NdotH2 - 1) / (r2NdotH2)) / (PI * r2NdotH2 * NdotH2);
}
BlinnPhong
来源[6],BlinnPhong公式纯粹是基于经验的,在恰当选取参数的情况下,它的函数曲线非常接近于Beckmann。
BlinnPhong原始的模型是:
D B l i n n ( h , α ) = χ + ( n , h ) α p + 2 2 π ( n ⋅ h ) α p D_{Blinn}({\bf{h}}, \alpha) = \chi^+({\bf{n}},{\bf{h}})\frac{\alpha_p + 2}{2\pi}({\bf{n}}\cdot{\bf{h}})^{\alpha_p} DBlinn(h,α)=χ+(n,h)2παp+2(n⋅h)αp
其中, α p \alpha_p αp表示粗糙系数,或者准确的说,是光滑系数—— α p \alpha_p αp越大,表示物体表面越光滑。
- 当 α p = ∞ \alpha_p=\infty αp=∞的时候,表示绝对光滑的物体,此时 D B l i n n ( h , α ) D_{Blinn}({\bf{h}}, \alpha) DBlinn(h,α)只有在 h = n {\bf{h}} = {\bf{n}} h=n,即入射角等于出射角的时候为 ∞ \infty ∞,否则为0。
- 当 α p = 0 \alpha_p=0 αp=0的时候,表示绝对粗糙的物体, D B l i n n ( h , α ) = 1 π D_{Blinn}({\bf{h}}, \alpha) = \frac{1}{\pi} DBlinn(h,α)=π1,这个式子也是后面会提到的diffuse的式子。
令 α p = ( 2 α 2 − 2 ) \alpha_p = (\frac{2}{\alpha^2} - 2) αp=(α22−2),则有:
D B l i n n ( h , α ) = χ + ( n , h ) π α 2 ( n ⋅ h ) ( 2 α 2 − 2 ) D_{Blinn}({\bf{h}}, \alpha) = \frac{\chi^+({\bf{n}},{\bf{h}})}{\pi\alpha^2}({\bf{n}}\cdot{\bf{h}})^{(\frac{2}{\alpha^2} - 2)} DBlinn(h,α)=πα2χ+(n,h)(n⋅h)(α22−2)
这个公式即接近于Beckmann的法向分布公式,也是常用的BlinnPhong形式。
shader实现:
float DistributionBlinnPhong(float NdotH, float r) {
float a = r * r;
return pow(NdotH, 2.0 / a - 2.0) / (PI * a);
}
GGX
来源[3],GGX是根据实测数据拟合出来的一个公式:
D G G X ( h , α ) = χ + ( n , h ) ⋅ α 2 π ( ( n ⋅ h ) 2 ( α 2 − 1 ) + 1 ) 2 D_{GGX}({\bf{h}}, \alpha) = \frac{\chi^+({\bf{n}},{\bf{h}})\cdot\alpha^2}{\pi(({\bf{n}}\cdot{\bf{h}})^2(\alpha^2-1)+1)^2} DGGX(h,α)=π((n⋅h)2(α2−1)+1)2χ+(n,h)⋅α2
shader实现:
float DistributionGGX(float NdotH, float r) {
float a2 = r * r;
float NdotH2 = NdotH * NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / max(denom, 0.001);
}
除了这三种公式,还有更多更复杂的法向分布函数D,具体可以参考[17]。但是其实最常用的还是GGX(及其各向异性模式),无论是游戏还是影视行业都比较喜欢用GGX。
GTR
Burley通过对Berry(与GGX公式类似,分母上的指数为1)和GGX公式的观察,提出了广义的Trowbridge-Reitz(Generalized-Trowbridge-Reitz,GTR)法线分布函数:
D G T R ( h , α ) = c ⋅ χ + ( n , h ) ( ( n ⋅ h ) 2 ( α 2 − 1 ) + 1 ) γ D_{GTR}({\bf{h}}, \alpha) = \frac{c\cdot\chi^+({\bf{n}},{\bf{h}})}{(({\bf{n}}\cdot{\bf{h}})^2(\alpha^2-1)+1)^\gamma} DGTR(h,α)=((n⋅h)2(α2−1)+1)γc⋅χ+(n,h)
其中, c c c表示缩放系数,是一个常数; γ \gamma γ用于控制尾部的形状,当 γ = 1 \gamma=1 γ=1的时候, D G T R D_{GTR} DGTR就是Berry公式,当 γ = 2 \gamma=2 γ=2的时候, D G T R D_{GTR} DGTR就是 D G G X D_{GGX} DGGX。
γ \gamma γ的取值对 D G T R D_{GTR} DGTR的影响如下图所示。
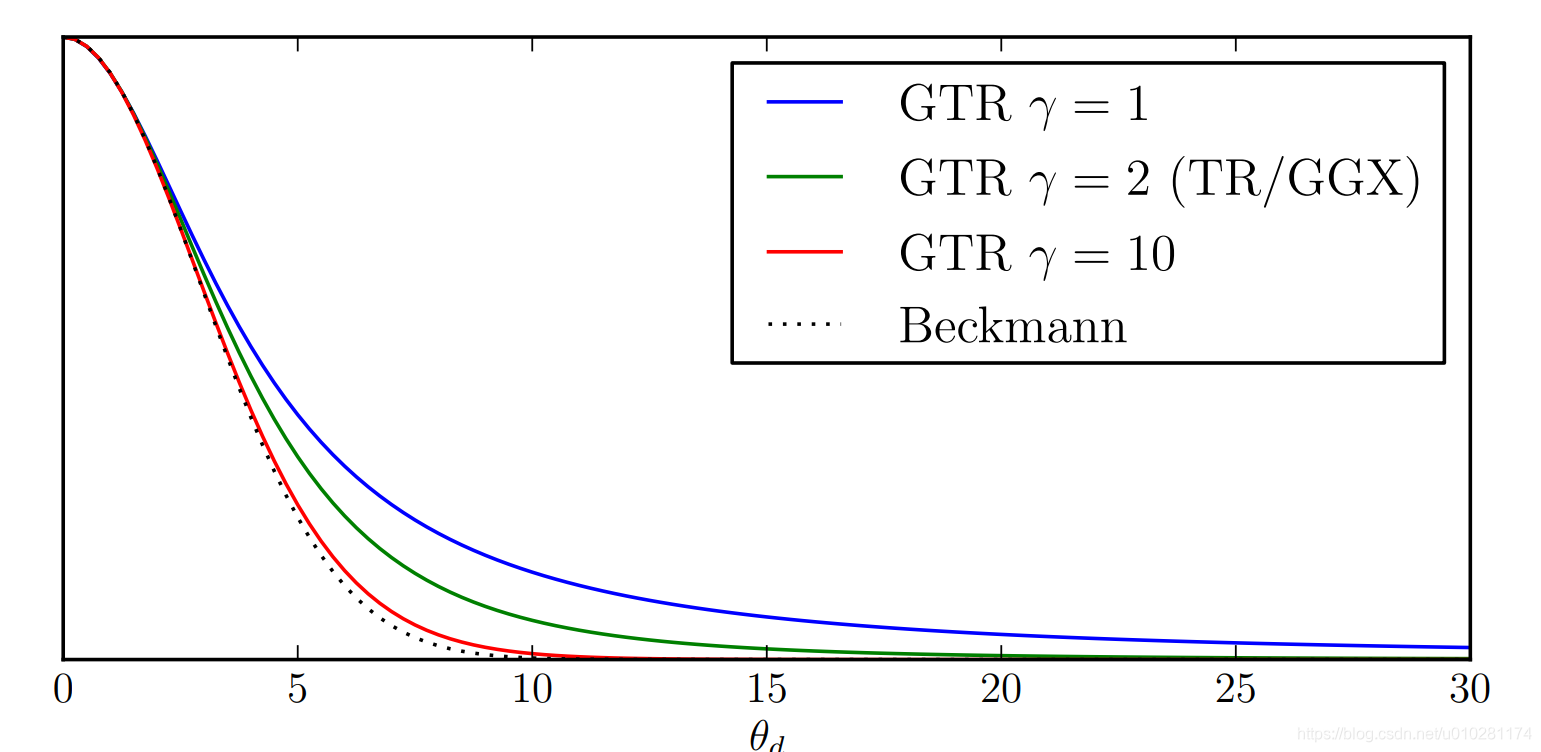
以下是 γ = 1 \gamma=1 γ=1和 γ = 2 \gamma=2 γ=2时的shader实现:
float DistributionGTR1(float NdotH, float r)
{
if (r >= 1) return 1/PI;
float a2 = r*r;
float t = 1 + (a2-1)*NdotH*NdotH;
return (a2-1) / (PI*log(a2)*t);
}
float DistributionGTR2(float NdotH, float r)
{
float a2 = r*r;
float t = 1 + (a2-1)*NdotH*NdotH;
return a2 / (PI * t * t);
}
效果对比

可以看出,BlinnPhong和Beckmann的差异不大。而GGX有着更平滑的边缘和更小的峰值。除此之外,GGX运算压力更小,因为它没有指数操作。
遮挡项 G
和法向分布函数 D D D一样,遮挡项 G G G也是入射角、出射角和表面粗糙度的函数。
有些文章会把遮挡项G和BRDF的分母 ( n ⋅ l ) ( n ⋅ v ) ({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}}) (n⋅l)(n⋅v)放在一起组成一项约分掉,这也是一种优化思路,因为G通常包含这两个cosine因子。这里我们约定本文的遮挡项 G G G是不约分 ( n ⋅ l ) ( n ⋅ v ) ({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}}) (n⋅l)(n⋅v)的 G G G。
Implicit
来源[7],有些BRDF公式会忽略遮挡项G,将其跟分母上的 ( n ⋅ l ) ( n ⋅ v ) ({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}}) (n⋅l)(n⋅v)一起忽略掉,这就有了第一个隐式 G G G:
G I m p l i c i t ( l , v , h ) = ( n ⋅ l ) ( n ⋅ v ) G_{Implicit}({\bf{l}},{\bf{v}},{\bf{h}})=({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}}) GImplicit(l,v,h)=(n⋅l)(n⋅v)
它的形态大概是,当且仅当视角和光源都垂直于物体表面的时候, G I m p l i c i t = 1 G_{Implicit}=1 GImplicit=1,光源、视角与物体表面法线的夹角越大, G I m p l i c i t G_{Implicit} GImplicit越小,直到衰减为0,这也是很符合常识的。
shader实现:
float GeometryImplicit(float NdotV, float NdotL) {
return NdotL * NdotV;
}
但是隐式遮挡项 G I m p l i c i t G_{Implicit} GImplicit最大的问题在于,它随着视角的衰减速度太快,这会使得高光区域太窄。为了解决这个问题,我们继续看显式的遮挡项 G G G。
Cook-Torrance
来源[9], G C o o k − T o r r a n c e G_{Cook-Torrance} GCook−Torrance解决了 G I m p l i c i t G_{Implicit} GImplicit衰减速度太快的问题:
G C o o k − T o r r a n c e ( l , v , h ) = min ( 1 , 2 ( n ⋅ h ) ( n ⋅ v ) v ⋅ h , 2 ( n ⋅ h ) ( n ⋅ l ) v ⋅ h ) G_{Cook-Torrance}({\bf{l}},{\bf{v}},{\bf{h}})=\min{\left(1, \frac{2({\bf{n}}\cdot{\bf{h}})({\bf{n}}\cdot{\bf{v}})}{{\bf{v}}\cdot{\bf{h}}}, \frac{2({\bf{n}}\cdot{\bf{h}})({\bf{n}}\cdot{\bf{l}})}{{\bf{v}}\cdot{\bf{h}}}\right)} GCook−Torrance(l,v,h)=min(1,v⋅h2(n⋅h)(n⋅v),v⋅h2(n⋅h)(n⋅l))
shader实现:
float GeometryCookTorrance(float NdotV, float NdotL, float VdotH, float NdotH) {
float ct1 = 2 * NdotH * NdotV / VdotH;
float ct2 = 2 * NdotH * NdotL / VdotH;
return min(1, min(ct1, ct2));
}
Kelemen
来源[10],也是解决 G I m p l i c i t G_{Implicit} GImplicit衰减速度太快的问题,同时 G K e l e m e n G_{Kelemen} GKelemen比 G C o o k − T o r r a n c e G_{Cook-Torrance} GCook−Torrance的效率更高:
G K e l e m e n ( l , v , h ) = ( n ⋅ l ) ( n ⋅ v ) ( v ⋅ h ) 2 G_{Kelemen}({\bf{l}},{\bf{v}},{\bf{h}})=\frac{({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}})}{({\bf{v}}\cdot{\bf{h}})^2} GKelemen(l,v,h)=(v⋅h)2(n⋅l)(n⋅v)
shader实现:
float GeometryKelemen(float NdotV, float NdotL, float VdotH) {
return NdotV * NdotL / (VdotH * VdotH);
}
Neumann
来源[8], G N e u m a n n G_{Neumann} GNeumann用另一种方式解决了 G I m p l i c i t G_{Implicit} GImplicit衰减速度太快的问题:
G N e u m a n n ( l , v , h ) = ( n ⋅ l ) ( n ⋅ v ) max ( n ⋅ l , n ⋅ v ) G_{Neumann}({\bf{l}},{\bf{v}},{\bf{h}})=\frac{({\bf{n}}\cdot{\bf{l}})({\bf{n}}\cdot{\bf{v}})}{\max{({\bf{n}}\cdot{\bf{l}}, {\bf{n}}\cdot{\bf{v}}})} GNeumann(l,v,h)=max(n⋅l,n⋅v)(n⋅l)(n⋅v)
shader实现:
float GeometryNeumann(float NdotV, float NdotL) {
return (NdotL * NdotV) / max(NdotL, NdotV);
}
但是,以上三个解决方案也不够完美。前面提到过,遮挡项G应该是入射角、出射角和表面粗糙度的函数,而以上四个G,包括隐式遮挡项都与粗糙度无关。
Smith
Smith家族[13]都是采用了前面介绍的 G 1 G_1 G1相乘的形式:
G 2 ( l , v , h ) = G 1 ( l ) G 1 ( v ) G_2({\bf{l}},{\bf{v}},{\bf{h}})=G_1({\bf{l}})G_1({\bf{v}}) G2(l,v,h)=G1(l)G1(v)
他们之间的区别就是 G 1 G_1 G1的选取不同。
Beckmann
Beckmann的 G G G是跟 D D D一起提出的,前面介绍过 G G G是可以从 D D D推导出来的,因此Beckmann的 Λ \Lambda Λ为:
c = n ⋅ v α 1 − ( n ⋅ v ) 2 Λ ( v ) = erf ( c ) − 1 2 + 1 2 c π exp ( − c 2 ) \begin{aligned} c & = \frac{{\bf{n}}\cdot{\bf{v}}}{\alpha\sqrt{1-({\bf{n}}\cdot{\bf{v}})^2}} \\ \Lambda({\bf{v}}) & = \frac{\text{erf}(c)-1}{2}+\frac{1}{2c\sqrt{\pi}}\exp(-c^2) \end{aligned} cΛ(v)=α1−(n⋅v)2n⋅v=2erf(c)−1+2cπ1exp(−c2)
但是由于有 erf \text{erf} erf函数的存在,计算起来过于复杂,因此通常用如下的近似形式:
Λ ( v ) ≈ { 1 − 1.259 x + 0.396 c 2 3.535 c + 2.181 c 2 , if c < 1.6 0 , if c ≥ 1.6 \Lambda({\bf{v}}) \approx \begin{cases} \frac{1-1.259x+0.396c^2}{3.535c+2.181c^2}, & \text{if }c<1.6 \\ 0, & \text{if }c\geq1.6 \end{cases} Λ(v)≈{3.535c+2.181c21−1.259x+0.396c2,0,if c<1.6if c≥1.6
因此,Beckmann的 G 1 G_1 G1为
G B e c k m a n n ( v ) ≈ { 3.535 c + 2.181 c 2 1 + 2.276 c + 2.577 c 2 , if c < 1.6 1 , if c ≥ 1.6 G_{Beckmann}({\bf{v}}) \approx \begin{cases} \frac{3.535c+2.181c^2}{1+2.276c+2.577c^2}, & \text{if }c<1.6 \\ 1, & \text{if }c\geq1.6 \end{cases} GBeckmann(v)≈{1+2.276c+2.577c23.535c+2.181c2,1,if c<1.6if c≥1.6
shader实现:
float GeometryBeckmann(float NdotV, float r) {
float c = NdotV / (r * sqrt(1 - NdotV * NdotV));
float c2 = c * c;
if (c < 1.6)
return (3.535 * c + 2.181 * c2) / (1 + 2.276 * c + 2.577 * c2);
else
return 1.0;
}
float GeometrySmithBeckmann(float NdotV, float NdotL, float r) {
float ggx2 = GeometryBeckmann(NdotV, r);
float ggx1 = GeometryBeckmann(NdotL, r);
return ggx1 * ggx2;
}
GGX
GGX[3]跟Beckmann类似,都是从法向分布函数推导出来的:
c = n ⋅ v α 1 − ( n ⋅ v ) 2 Λ ( v ) = − 1 + 1 + 1 c 2 2 \begin{aligned} c & = \frac{{\bf{n}}\cdot{\bf{v}}}{\alpha\sqrt{1-({\bf{n}}\cdot{\bf{v}})^2}} \\ \Lambda({\bf{v}}) & = \frac{-1+\sqrt{1+\frac{1}{c^2}}}{2} \end{aligned} cΛ(v)=α1−(n⋅v)2n⋅v=2−1+1+c21
对应的 G 1 G_1 G1定义为
G G G X ( v ) = 2 ( n ⋅ v ) ( n ⋅ v ) + α 2 + ( 1 − α 2 ) ( n ⋅ v ) 2 G_{GGX}({\bf{v}}) = \frac{2({\bf{n}}\cdot{\bf{v}})}{({\bf{n}}\cdot{\bf{v}})+\sqrt{\alpha^2+(1-\alpha^2)({\bf{n}}\cdot{\bf{v}})^2}} GGGX(v)=(n⋅v)+α2+(1−α2)(n⋅v)22(n⋅v)
shader实现:
float GeometryGGX(float NdotV, float r) {
float r2 = r * r;
return (2 * NdotV) / (NdotV + sqrt(r2 + (1 - r2) * NdotV * NdotV));
}
float GeometrySmithGGX(float NdotV, float NdotL, float r) {
float ggx2 = GeometryGGX(NdotV, r);
float ggx1 = GeometryGGX(NdotL, r);
return ggx1 * ggx2;
}
GGX Joint
前面提到的GGX用的是 G 2 = G 1 ∗ G 1 G_2=G_1*G_1 G2=G1∗G1的separable G,如果用height-correlated G,那么 G 2 G_2 G2变为:
G 2 − G G X J o i n t ( l , v , m ) = 1 1 + Λ ( l ) + Λ ( v ) = 2 ( n ⋅ v ) ( n ⋅ l ) ( n ⋅ l ) ⋅ α 2 + ( 1 − α 2 ) ( n ⋅ v ) 2 + ( n ⋅ v ) ⋅ α 2 + ( 1 − α 2 ) ( n ⋅ l ) 2 \begin{aligned} G_{2-GGXJoint}({\bf{l}},{\bf{v}},{\bf{m}}) & =\frac{1}{1+\Lambda({\bf{l}})+\Lambda({\bf{v}})}\\ & =\frac{2({\bf{n}}\cdot{\bf{v}})({\bf{n}}\cdot{\bf{l}})}{({\bf{n}}\cdot{\bf{l}})\cdot\sqrt{\alpha^2+(1-\alpha^2)({\bf{n}}\cdot{\bf{v}})^2} + ({\bf{n}}\cdot{\bf{v}})\cdot\sqrt{\alpha^2+(1-\alpha^2)({\bf{n}}\cdot{\bf{l}})^2}} \end{aligned} G2−GGXJoint(l,v,m)=1+Λ(l)+Λ(v)1=(n⋅l)⋅α2+(1−α2)(n⋅v)2+(n⋅v)⋅α2+(1−α2)(n⋅l)22(n⋅v)(n⋅l)
shader实现:
float GeometrySmithGGXJoint(float NdotV, float NdotL, float r) {
float r2 = r * r;
float Vis_SmithV = NdotL * sqrt(NdotV * (NdotV - NdotV * r2) + r2);
float Vis_SmithL = NdotV * sqrt(NdotL * (NdotL - NdotL * r2) + r2);
return 2 * NdotV * NdotL / (Vis_SmithV + Vis_SmithL);
}
为了提高计算效率,UE4对GGX Joint方法做了一个近似,公式为:
G 2 − G G X J o i n t ( l , v , m ) = 1 1 + Λ ( l ) + Λ ( v ) ≈ 2 ( n ⋅ v ) ( n ⋅ l ) ( n ⋅ l ) ⋅ ( α + ( 1 − α ) ( n ⋅ v ) ) + ( n ⋅ v ) ⋅ ( α + ( 1 − α ) ( n ⋅ l ) ) \begin{aligned} G_{2-GGXJoint}({\bf{l}},{\bf{v}},{\bf{m}}) & =\frac{1}{1+\Lambda({\bf{l}})+\Lambda({\bf{v}})}\\ & \approx\frac{2({\bf{n}}\cdot{\bf{v}})({\bf{n}}\cdot{\bf{l}})}{({\bf{n}}\cdot{\bf{l}})\cdot(\alpha+(1-\alpha)({\bf{n}}\cdot{\bf{v}})) + ({\bf{n}}\cdot{\bf{v}})\cdot(\alpha+(1-\alpha)({\bf{n}}\cdot{\bf{l}}))} \end{aligned} G2−GGXJoint(l,v,m)=1+Λ(l)+Λ(v)1≈(n⋅l)⋅(α+(1−α)(n⋅v))+(n⋅v)⋅(α+(1−α)(n⋅l))2(n⋅v)(n⋅l)
shader实现:
float GeometryGGXJointApprox(float NdotV, float NdotL, float r) {
return (NdotV) / (NdotL * (r + (1 - r) * NdotV));
}
float GeometrySmithGGXJointApprox(float NdotV, float NdotL, float r) {
float Vis_SmithV = NdotL * ( NdotV * ( 1 - r ) + r );
float Vis_SmithL = NdotV * ( NdotL * ( 1 - r ) + r );
return 2 * NdotV * NdotL / ( Vis_SmithV + Vis_SmithL );
}
Schlick-Beckmann
Schlick[11]的
G
1
G_1
G1定义为
k
=
α
2
π
G
S
c
h
l
i
c
k
(
v
)
=
n
⋅
v
(
n
⋅
v
)
(
1
−
k
)
+
k
k=\alpha\sqrt{\frac{2}{\pi}} \\ G_{Schlick}({\bf{v}})=\frac{{\bf{n}}\cdot{\bf{v}}}{({\bf{n}}\cdot{\bf{v}})(1-k)+k}
k=απ2GSchlick(v)=(n⋅v)(1−k)+kn⋅v
shader实现:
float GeometrySchlickBeckmann(float NdotV, float r) {
float k = (r)*sqrt(2.0 / PI);
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmithSchlickBeckmann(float NdotV, float NdotL, float r) {
float ggx2 = GeometrySchlickBeckmann(NdotV, r);
float ggx1 = GeometrySchlickBeckmann(NdotL, r);
return ggx1 * ggx2;
}
Schlick-GGX
Schlick-GGX[12]曾经是UE4所采用的的一个模型,跟Schlick有些类似,
G
1
G_1
G1定义为
k
=
α
2
G
S
c
h
l
i
c
k
(
v
)
=
n
⋅
v
(
n
⋅
v
)
(
1
−
k
)
+
k
k=\frac{\alpha}{2} \\ G_{Schlick}({\bf{v}})=\frac{{\bf{n}}\cdot{\bf{v}}}{({\bf{n}}\cdot{\bf{v}})(1-k)+k}
k=2αGSchlick(v)=(n⋅v)(1−k)+kn⋅v
shader实现:
float GeometrySchlickGGX(float NdotV, float r) {
float k = r * 0.5;
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmithSchlickGGX(float NdotV, float NdotL, float r) {
float ggx2 = GeometrySchlickGGX(NdotV, r);
float ggx1 = GeometrySchlickGGX(NdotL, r);
return ggx1 * ggx2;
}
这里面还有一个细节,那就是迪士尼后来提出了对粗糙粗roughness做一个remapping,使得它更接近于真实:
α
′
=
(
r
o
u
g
h
n
e
s
s
+
1
2
)
2
\alpha' = (\frac{roughness + 1}{2})^2 \\
α′=(2roughness+1)2
其他的部分不变。这样shader实现为:
float GeometrySmithSchlickGGX(float NdotV, float NdotL, float roughness) {
float r = (roughness + 1.0) * 0.5; // remapping roughness
r = r * r
float ggx2 = GeometrySchlickGGX(NdotV, r);
float ggx1 = GeometrySchlickGGX(NdotL, r);
return ggx1 * ggx2;
}
注意,此时GeometrySmithSchlickGGX的输入参数不是r,而改为了roughness。
优化
考虑到几乎所有
G
G
G都带有
(
n
⋅
v
)
(
n
⋅
l
)
({\bf{n}}\cdot{\bf{v}})({\bf{n}}\cdot{\bf{l}})
(n⋅v)(n⋅l)项,可以跟
f
r
(
l
,
v
)
f_r({\bf{l}},{\bf{v}})
fr(l,v)的分母约分,因此在实现时,可以考虑定义
G
′
=
G
(
n
⋅
v
)
(
n
⋅
l
)
G'=\frac{G}{({\bf{n}}\cdot{\bf{v}})({\bf{n}}\cdot{\bf{l}})}
G′=(n⋅v)(n⋅l)G
节省一部分计算。
这样做不只是出于性能的考虑,也是出于精度的考虑。如果 n ⋅ v {\bf{n}}\cdot{\bf{v}} n⋅v和 n ⋅ l {\bf{n}}\cdot{\bf{l}} n⋅l的乘积接近于0,那么specular项的分母会非常小,严重影响其精度,极端的情况下会在过渡区域产生一道割裂的分界线。下图展示了 ( n ⋅ v ) ∗ ( n ⋅ l ) ∗ 10 ({\bf{n}}\cdot{\bf{v}})*({\bf{n}}\cdot{\bf{l}})*10 (n⋅v)∗(n⋅l)∗10(左)、未优化时(中)、优化后(右)的效果,可以看出左侧两张图的分界线非常吻合。优化后则没有颜色割裂的问题。

效果对比
取roughness = 0.9,计算球体的遮挡项效果为:

最后一排是常用的几种方法,差异并不大,边缘的过渡也比较好。
菲涅尔项 F
菲涅尔项描述的是物体表面的反射、折射现象。一般我们会采用常量 F 0 F_0 F0来计算菲涅尔项 F ( v , h , F 0 ) F({\bf{v}},{\bf{h}},F_0) F(v,h,F0)。
要说明白菲涅尔项,得从光学在介质表面的折射反射现象说起。我们知道光线会在介质表面产生不连续性,具体表现为一部分光线反射——遵循光线反射定律,入射角等于反射角;另一部分光线会折射进入介质——遵循光线折射定律,折射角取决于入射角的大小以及构成交界面的两种材质,即斯涅耳定律(Snell’s law):
n 1 sin ( θ i ) = n 2 sin ( θ t ) n_1\sin(\theta_i)=n_2\sin(\theta_t) n1sin(θi)=n2sin(θt)
斯涅耳定律描述的仅仅是光线的角度,但是图形学研究的其实是光线的radiance/irradiance,所以我们要更进一步。定义Fresnel reflectance
R
F
R_F
RF为反射光线的radiance占入射光线radiance的比例,
R
F
R_F
RF是入射角
θ
i
\theta_i
θi的函数。那么对于入射光线
L
i
L_i
Li,在角度
θ
i
\theta_i
θi时反射光线的radiance为
R
F
(
θ
i
)
L
i
R_F(\theta_i)L_i
RF(θi)Li。再考虑折射部分,根据能量守恒,没有反射的能量都会被折射(不考虑被吸收的能量),因此折射的flux占入射flux的比例是
1
−
R
F
1-R_F
1−RF。这里需要强调的是,radiance定义的是“irradiance每立体角”,它的大小跟角度有关系,因此折射光线的radiance
L
t
L_t
Lt不能简单用
1
−
R
F
1-R_F
1−RF乘上
L
i
L_i
Li,而要转换角度:
L
t
=
(
1
−
R
F
(
θ
i
)
)
sin
2
θ
i
sin
2
θ
t
L
i
L_t = (1-R_F(\theta_i))\frac{\sin^2\theta_i}{\sin^2\theta_t}L_i
Lt=(1−RF(θi))sin2θtsin2θiLi
将斯涅耳定律带入上式,得到:
L
t
=
(
1
−
R
F
(
θ
i
)
)
n
2
2
n
1
2
L
i
L_t = (1-R_F(\theta_i))\frac{n_2^2}{n_1^2}L_i
Lt=(1−RF(θi))n12n22Li
介绍了这么多
R
F
R_F
RF的相关知识,其实关键点还是前面说的,
R
F
R_F
RF是入射角
θ
i
\theta_i
θi的函数。我们再回头考虑这个
R
F
R_F
RF与入射角
θ
i
\theta_i
θi的关系。当
θ
i
=
90
°
\theta_i=90\degree
θi=90°的时候,即
R
F
(
90
°
)
R_F(90\degree)
RF(90°),此时入射光平行于平面,垂直于法向,不存在折射光线,
R
F
(
90
°
)
=
1
R_F(90\degree)=1
RF(90°)=1;当
θ
i
=
0
°
\theta_i=0\degree
θi=0°的时候,即
R
F
(
0
°
)
R_F(0\degree)
RF(0°),此时反射光线占比最低,根据不同的材质这个
R
F
(
0
°
)
R_F(0\degree)
RF(0°)有不同的值,Real-time Rendering[14]给出了常见的材质的
R
F
R_F
RF与
θ
i
\theta_i
θi的关系曲线:
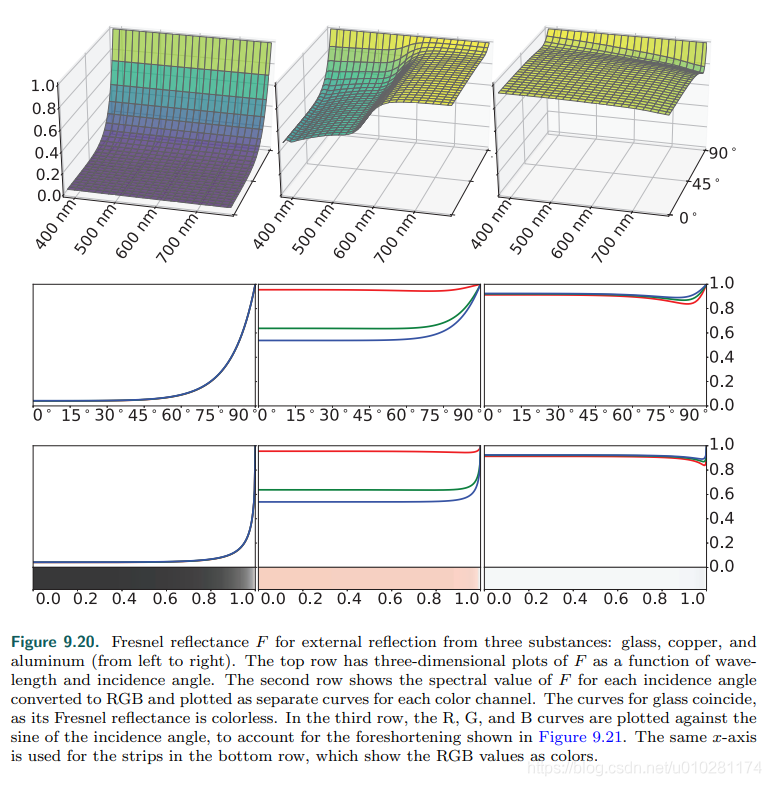
为了近似这个曲线,采取的策略是利用
R
F
(
0
°
)
R_F(0\degree)
RF(0°),也就是前面说的
F
0
F_0
F0:
R
F
(
θ
i
)
≈
R
F
(
0
°
)
+
(
1
−
R
F
(
0
°
)
)
(
1
−
cos
θ
i
)
5
R_F(\theta_i)\approx R_F(0\degree) + (1-R_F(0\degree))(1-\cos\theta_i)^5
RF(θi)≈RF(0°)+(1−RF(0°))(1−cosθi)5
这里有一个默认的假设是,
R
F
(
90
°
)
=
1
R_F(90\degree)=1
RF(90°)=1,如果,
R
F
(
90
°
)
R_F(90\degree)
RF(90°)未知,
R
F
(
θ
i
)
R_F(\theta_i)
RF(θi)应该写为:
R
F
(
θ
i
)
≈
R
F
(
0
°
)
+
(
R
F
(
90
°
)
−
R
F
(
0
°
)
)
(
1
−
cos
θ
i
)
5
R_F(\theta_i)\approx R_F(0\degree) + (R_F(90\degree)-R_F(0\degree))(1-\cos\theta_i)^5
RF(θi)≈RF(0°)+(RF(90°)−RF(0°))(1−cosθi)5
这个
R
F
(
90
°
)
R_F(90\degree)
RF(90°)也就是
F
90
F_{90}
F90。
最后,我们看一下
F
0
F_0
F0怎么计算。对于dielectrics来说,
F
0
F_0
F0的值取决于折射率,公式为:
F
0
=
0.16
⋅
r
e
f
l
e
c
t
a
n
c
e
2
F_0=0.16\cdot reflectance^2
F0=0.16⋅reflectance2
其中,
r
e
f
l
e
c
t
a
n
c
e
reflectance
reflectance由物体表面的材质定义。
对于conductors,
F
0
F_0
F0通过金属度metallic和basecolor来计算:
F
0
=
b
a
s
e
C
o
l
o
r
⋅
m
e
t
a
l
l
i
c
F_0=baseColor\cdot metallic
F0=baseColor⋅metallic
综合dielectrics和dielectric,得到:
vec3 F0 = 0.16 * reflectance * reflectance * (1.0 - metallic) + baseColor.xyz * metallic;
说明白了 F 0 F_0 F0,我们接下来看看菲涅尔函数 F F F有哪些形式。
简单形式
最简单的情况,直接令菲涅尔函数等于
F
0
F_0
F0:
F
N
o
n
e
(
v
,
h
)
=
F
0
F_{None}({\bf{v}},{\bf{h}})=F_0
FNone(v,h)=F0
shader实现:
vec3 Fresnel(vec3 F0) {
return F0;
}
Schlick
来源[11],公式:
F
S
c
h
l
i
c
k
(
v
,
h
)
=
F
0
+
(
1
−
F
0
)
(
1
−
(
v
⋅
h
)
)
5
F_{Schlick}({\bf{v}},{\bf{h}})=F_0+(1-F_0)(1-({\bf{v}}\cdot{\bf{h}}))^5
FSchlick(v,h)=F0+(1−F0)(1−(v⋅h))5
也就是我们前面说到的对
R
F
R_F
RF的拟合。shader实现:
vec3 FresnelSchlick(float VdotH, vec3 F0) {
return F0 + (1.0 - F0) * pow(1.0 - VdotH, 5.0);
}
如果引入
F
90
F_{90}
F90,则变成:
F
S
c
h
l
i
c
k
(
v
,
h
)
=
F
0
+
(
F
90
−
F
0
)
(
1
−
(
v
⋅
h
)
)
5
F_{Schlick}({\bf{v}},{\bf{h}})=F_0+(F_{90}-F_0)(1-({\bf{v}}\cdot{\bf{h}}))^5
FSchlick(v,h)=F0+(F90−F0)(1−(v⋅h))5
shader实现:
vec3 FresnelSchlick(float VdotH, vec3 F0, vec F90) {
return F0 + (F90 - F0) * pow(1.0 - VdotH, 5.0);
}
对specular来说, F 90 F_{90} F90可以从 F 0 F_0 F0计算得来[1]:
float F90 = saturate(dot(F0, vec3(50.0 * 0.33)));
Cook-Torrance
来源[9],公式:
η
=
1
+
F
0
1
−
F
0
c
=
v
⋅
h
g
=
η
2
+
c
2
−
1
F
C
o
o
k
−
T
o
r
r
a
n
c
e
(
v
,
h
)
=
1
2
(
g
−
c
g
+
c
)
2
(
1
+
(
(
g
+
c
)
c
−
1
(
g
−
c
)
c
+
1
)
2
)
\begin{aligned} \eta & =\frac{1+\sqrt{F_0}}{1-\sqrt{F_0}} \\ c & = {\bf{v}}\cdot{\bf{h}} \\ g & = \sqrt{\eta^2+c^2-1} \\ F_{Cook-Torrance}({\bf{v}},{\bf{h}}) & =\frac{1}{2}\left(\frac{g-c}{g+c}\right)^2\left(1+\left(\frac{(g+c)c-1}{(g-c)c+1}\right)^2\right) \end{aligned}
ηcgFCook−Torrance(v,h)=1−F01+F0=v⋅h=η2+c2−1=21(g+cg−c)2(1+((g−c)c+1(g+c)c−1)2)
shader实现:
float FresnelCookTorrance(float VdotH, float F0) {
float sqrtF = sqrt(F0);
float Eta = (1.0 + sqrtF) / (1.0 - sqrtF);
float g = sqrt(Eta * Eta + VdotH * VdotH - 1.0);
return 0.5 * pow((g - VdotH) / (g + VdotH), 2) *
(1 + pow(((g + VdotH) * VdotH - 1.0) / ((g - VdotH) * VdotH + 1.0), 2));
}
Diffuse BRDF
相比于繁琐的specular部分,diffuse部分就简单的多。diffuse部分由baseColor和diffuse系数相乘得到,即:
L
d
(
v
)
=
c
d
i
f
f
⋅
f
d
L_d({\bf{v}})={\bf{c}}_{diff}\cdot f_d
Ld(v)=cdiff⋅fd
shader实现:
vec3 colorDiffuse = baseColor * DiffuseBRDF(NdotV, NdotL, LdotH, roughness);
接下来看一下 f d f_d fd的可能取值。
Lambert
Lambert模型认为既然diffuse是漫反射,不如简单地认为各个方向都是一样的值,即出射光线的radiance与入射光线的角度无关。
f d = 1 π f_d = \frac{1}{\pi} fd=π1
这个实现相当于,采用BlinnPhong的法向分布 D B l i n n ( h , α ) = 1 π D_{Blinn}({\bf{h}}, \alpha) = \frac{1}{\pi} DBlinn(h,α)=π1,同时令遮挡项为隐式形式,并且菲涅尔项为1。虽然简单,但是已经足够近似现实了,效果还不错。
shader实现:
float DiffuseLambert() {
return 1.0 / PI;
}
虽然Lambert模型已经足够接近真实情况,但是它还是不够理想。我们前面提到过,diffuse分量本质上是光线折射进入物体表面,经过多次反射再折射出来的现象,也就是它不是物理上真实存在的一个光学现象。而在讨论specular菲涅尔项的时候又提到过,反射部分会随着入射光线的角度变化,那么折射部分相应的也会随着入射角度变化,既然如此,来自于折射部分的diffuse分量肯定也是会随着入射光线的角度而改变的!也就是说, f d f_d fd是入射角 l {\bf{l}} l的函数: f d ( l ) f_d({\bf{l}}) fd(l)。
同时, f d f_d fd也应该是出射角 v {\bf{v}} v的函数[14]: f d ( l , v ) f_d({\bf{l}},{\bf{v}}) fd(l,v)。因为菲涅尔项考虑的是镜面反射,入射角等于出射角,而diffuse项的入射角不一定等于出射角,因此两个角度都会影响 f d f_d fd。
再者,前面影响specular分量的参数当中, r o u g h n e s s roughness roughness也会影响 f d f_d fd。根据常识,不同粗糙程度的物体的diffuse是有明显的不同的。即 f d ( l , v , r o u g h n e s s ) f_d({\bf{l}}, {\bf{v}}, roughness) fd(l,v,roughness)。
基于这一点洞察,又有一些新的diffuse模型被提出,希望解决Lambert模型的不足。。
Oren–Nayar
Oren-Nayar模型是对Lambert模型的推广。[18]指出,Lambert模型对于光滑物体或许还成立,但是对于粗糙物体是不正确的。粗糙的物体在光照下会显得很平坦,而Lambert模型没有表现出这种平坦。为了达到这个效果,Oren-Nayar加强了掠射逆反射(入射角和出射角在几乎同一个方向,并且垂直于法向的情形)的强度。
Oren-Nayar公式如下。
f d = 1 π ⋅ ( A + B ⋅ max ( 0 , cos ϕ ) ⋅ sin α ⋅ tan β ) A = 1.0 − 0.5 α α + 0.33 B = 0.45 α α + 0.09 α = max ( l ⋅ n , v ⋅ n ) β = min ( l ⋅ n , v ⋅ n ) \begin{aligned} f_d & = \frac{1}{\pi}\cdot(A+B\cdot\max{(0, \cos{\phi})}\cdot\sin\alpha\cdot\tan\beta) \\ A & = 1.0-0.5\frac{\alpha}{\alpha+0.33} \\ B & = 0.45\frac{\alpha}{\alpha+0.09} \\ \alpha & = \max{({\bf{l}}\cdot{\bf{n}}, {\bf{v}}\cdot{\bf{n}})} \\ \beta & = \min{({\bf{l}}\cdot{\bf{n}}, {\bf{v}}\cdot{\bf{n}})} \end{aligned} fdABαβ=π1⋅(A+B⋅max(0,cosϕ)⋅sinα⋅tanβ)=1.0−0.5α+0.33α=0.45α+0.09α=max(l⋅n,v⋅n)=min(l⋅n,v⋅n)
其中, ϕ \phi ϕ表示 l n {\bf{l}}{\bf{n}} ln平面和 v n {\bf{v}}{\bf{n}} vn的夹角。
可以看出,当 r o u g h n e s s − 0 roughness-0 roughness−0的时候, A = 1 , B = 0 A=1, B=0 A=1,B=0,此时Oren-Nayar模型退化为Lambert模型。
下图[18]展示了真实照片、Lambert模型与Oren-Nayar的对比。

Hanrahan-Krueger
Hanrahan-Krueger模型[19]其实是源自次表面散射理论,是用于表现次表面散射现象的一个模型。它跟Oren-Nayar模型一样,对掠射角进行了补偿。但是它的补偿过于平坦,没有给出足够强的峰值,也不太完美。
Hanrahan-Krueger模型和Oren-Nayar模型都不太常用,因此不再赘述。
Burley
Oren–Nayar模型虽然提高了粗糙物体的真实性,但是它对掠射逆反射现象的修正还是不够真实。为了研究真实材料的物理特性,我们需要一个材质数据库。
MERL BRDF Database就是这样一个数据库。它是由MERL(Mitsubishi Electric Research Laboratories)实验室建立了的,测量并记录了不同角度的光源、观测视角情况下的BRDF数值,考虑到各向异性,每个材质都采样了90(光源)*90(视角)*180(各向异性)三个维度的数据。如果只考虑各向同性材质,可以将BRDF数据压缩到一张图片里。

如上图所示,横轴 θ h \theta_h θh表示half vector h {\bf{h}} h与法向量 n {\bf{n}} n之间的夹角。纵轴表示入射角与 h {\bf{h}} h的夹角。
Disney通过分析MERL BRDF Database,提出了两个Lambert模型与事实不符的地方:
- diffuse也会有类似于specular的光斑;
- 部分材质的diffuse会在掠射角有明显的光环,这个现象即掠射逆反射(grazing retroreflection);
为了解决这些问题,Disney提出了一个diffuse BRDF公式[15]:
f d ( l , v ) = 1 π F S c h l i c k ( n , l , 1 , f 90 ) F S c h l i c k ( n , v , 1 , f 90 ) F S c h l i c k ( n , l , f 0 , f 90 ) = F 0 + ( F 90 − F 0 ) ( 1 − ( n ⋅ l ) ) 5 f 90 = 0.5 + 2 ⋅ r o u g h n e s s ⋅ cos 2 ( θ d ) \begin{aligned} f_d({\bf{l}},{\bf{v}}) & = \frac{1}{\pi}F_{Schlick}({\bf{n}},{\bf{l}},1,f_{90})F_{Schlick}({\bf{n}},{\bf{v}},1,f_{90}) \\ F_{Schlick}({\bf{n}},{\bf{l}},f_0,f_{90}) & = F_0+(F_{90}-F_0)(1-({\bf{n}}\cdot{\bf{l}}))^5 \\ f_{90} & = 0.5 + 2\cdot roughness\cdot\cos^2(\theta_d) \end{aligned} fd(l,v)FSchlick(n,l,f0,f90)f90=π1FSchlick(n,l,1,f90)FSchlick(n,v,1,f90)=F0+(F90−F0)(1−(n⋅l))5=0.5+2⋅roughness⋅cos2(θd)
其中 θ d \theta_d θd是光线 L L L和half vector h h h的夹角。这个公式考虑到了入射角和出射角以及粗糙度,并且用类似菲涅尔项的公式(cosine项的五次方)来拟合衰减情况。
shader实现:
float FresnelSchlick(float VdotH, float F0, float F90) {
return F0 + (F90 - F0) * pow(1.0 - VdotH, 5.0);
}
float DiffuseBurley(float NdotV, float NdotL, float LdotH, float roughness) {
float f90 = 0.5 + 2.0 * roughness * LdotH * LdotH;
float lightScatter = FresnelSchlick(NdotL, 1.0, f90);
float viewScatter = FresnelSchlick(NdotV, 1.0, f90);
return lightScatter * viewScatter * (1.0 / PI);
}
总结
BRDF作为渲染里边最基础的知识点,发展的已经相对成熟,虽然偶尔也会有一些改进,但是基本上都是在效率与性能之间做权衡。对于基本BRDF公式的选择,UE4和Disney有着各自不同的逻辑:
Diffuse BRDF Distribution Visibility Fresnel UE4 L a m b e r t GGX G G X J o i n t ( A p p r o x ) Schlick Disney B u r l e y GGX G G X Schlick \begin{array}{c|ccccc} & \text{Diffuse BRDF} & \text{Distribution} & \text{Visibility} & \text{Fresnel} \\ \hline \text{UE4} & Lambert & \text{GGX} & GGX Joint(Approx) & \text{Schlick} \\ \text{Disney} & Burley & \text{GGX} & GGX & \text{Schlick} \end{array} UE4DisneyDiffuse BRDFLambertBurleyDistributionGGXGGXVisibilityGGXJoint(Approx)GGXFresnelSchlickSchlick
斜体表示二者不同的部分。可以看出,UE4选择的都是高效的模型,而Disney选择的都是复杂而准确的模型。
个人理解这些差异都是源于UE4和disney应用场景的不同,UE4希望每个模型尽可能高效,因此会拆分开来,针对性优化,比如它单独设计了针对眼睛的Eye模型,专门渲染毛发的Hair模型,专门渲染皮肤的subsurface模型等等。而Disney的诉求在于模型的表达力要足够强,效率反而不那么重要。
未涉及话题…
本文主要集中在BRDF项的各种实现,顺带介绍了BRDF和微表面理论。还有一些与之相关或更深入,但是没有涉及到的方向,例如
- 辐射度量学基础;
- BSDF,BTDF等BRDF的进阶模型;
- 各向异性BRDF,subsurface、clearCoat等模型;
- 环境光、全局光照等;
篇幅问题,这些方向也无法展开。行文至此,强推图形学届的武林秘籍的目录——Real-time Rendering,此书目前已经出到第四版了,文末也给出了电子书链接[14]。本文涉及的话题书中都有比较深入、全面的介绍。即使RTR不能满足你,它还提供了多达1000+篇的参考文献供学习,毕竟“目录”,名副其实。
参考资料
- Filament文档,Filament是一个Google写的用在Android上的PBR渲染器,它的文档非常完善,特别每个BRDF的理论和实现。同时也可以参考它的源码,对照学习。
- Specular BRDF Reference:这个博客列出了几大主流specular BRDF的公式,可以作为参考。
- Walter et al. 2007, Microfacet models for refraction through rough surfaces
- LearningOpenGL: PBR Theory:这也是一个不错的学习PBR的教材,有一个PBR的OpenGL实现,以及简单的理论介绍。
- Beckmann 1963, The scattering of electromagnetic waves from rough surfaces
- Blinn 1977, Models of light reflection for computer synthesized pictures
- Hoffman 2013, Background: Physics and Math of Shading
- Neumann et al. 1999, Compact metallic reflectance models
- Cook and Torrance 1982, A Reflectance Model for Computer Graphics
- Kelemen 2001, A microfacet based coupled specular-matte brdf model with importance sampling
- Schlick 1994, An Inexpensive BRDF Model for Physically-Based Rendering
- Karis 2013, Real Shading in Unreal Engine 4
- Smith 1967, Geometrical shadowing of a random rough surface
- Real-time Rendering, 4th edition,需要说明的一点是,此书的第四版比第三版增加了很多对BRDF公式的推导和历史介绍,更具有参考价值。
- Brent Burley. 2012. Physically Based Shading at Disney. Physically Based Shading in Film and Game Production, ACM SIGGRAPH 2012 Courses.
- Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs
- SIGGRAPH 2013 Course, Background: Physics and Math of Shading
- Generalization of Lambert’s reflectance model
- Reflection from Layered Surfaces due to Subsurface Scattering
- SIGGRAPH 2013 Course, Physically Based Shading at Disney
- PBR Diffuse Lighting for GGX+Smith Microsurfaces





















 1561
1561











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








