An Easy Problem?!
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 9363 | Accepted: 1385 |
Description
It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.
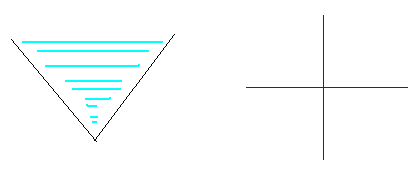
Your mission is to calculate how much rain these two boards can collect.

Your mission is to calculate how much rain these two boards can collect.
Input
The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x 1, y 1, x 2, y 2, x 3, y 3, x 4, y 4. ( x 1, y 1), ( x 2, y 2) are the endpoints of one board, and ( x 3, y 3), ( x 4, y 4) are the endpoints of the other one.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x 1, y 1, x 2, y 2, x 3, y 3, x 4, y 4. ( x 1, y 1), ( x 2, y 2) are the endpoints of one board, and ( x 3, y 3), ( x 4, y 4) are the endpoints of the other one.
Output
For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.
Sample Input
2 0 1 1 0 1 0 2 1 0 1 2 1 1 0 1 2
Sample Output
1.00 0.00 //这道题目看似容易,可是不知道坑死多少人,杀死我多少脑细胞,花了整整两天才AC了,简直凶残!!!
#include<iostream> #include<queue> #include<cstdio> #include<cstring> #include<string> #include<cmath> #include<algorithm> //#define eps le-8 const double eps=1e-8; const double INF=9999999; const double inf=7777777; using namespace std; typedef struct Node { double x; double y; }point; point p[4]; int sign(double x) { return (x>eps)-(x<-eps); } double Distance(point p1,point p2)// 返回两点之间欧氏距离 { return( sqrt( (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y) ) ); } double xmult(point p0,point p1,point p2)//叉积 { //cout<<p0.x<<" "<<p0.y<<" "<<p1.x<<" "<<p1.y<<" "<<p2.x<<" "<<p2.y<<endl; double p=(p1.x-p0.x)*(p2.y-p0.y);//WA20多次输出无数次中间结果才发现叉积直接返回会出问题(会出现莫名其妙的值),不信可以拿样例六测试下,会发现当你判断有没有交点直接返回没有,其实是有(2,2)这个交点 double q=-(p2.x-p0.x)*(p1.y-p0.y);//建议以后叉积都这样写(不会损失精度,因为你返回的值也是double) return p+q; } //相交返回true,否则为false,接口为两线段的端点 bool IsIntersected(point s1,point e1,point s2,point e2)//判断是否相交 { return (max(s1.x,e1.x)>=min(s2.x,e2.x))&& (max(s2.x,e2.x)>=min(s1.x,e1.x))&&(max(s1.y,e1.y)>=min(s2.y,e2.y))&&(max(s2.y,e2.y)>=min(s1.y,e1.y))&&(sign(xmult(s1,s2,e1))*sign(xmult(s1,e1,e2))>=0)&&(sign(xmult(s2,s1,e2))*sign(xmult(s2,e2,e1))>=0); } //计算两直线交点,注意事先判断直线是否平行! //线段交点请另外判线段相交(同时还是要判断是否平行!) point Intersection(point u1,point u2,point v1,point v2)//如果相交返回交点 { point res=u1; double a=(u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x); double b=(u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x); if(sign(b)==0)//这里要特判下,如果除数是0,证明两条线段斜率一样并且至少重合一个公共点 { res.x==INF; res.y==INF; } else { double t=a/b; res.x+=(u2.x-u1.x)*t; res.y+=(u2.y-u1.y)*t; } return res; } bool Same(point u1,point u2,point v1,point v2)//如果是同一条线段 { if((sign(u1.y-u2.y)==0)&&(sign(u1.y-v1.y)==0)&&(sign(v1.y-v2.y)==0)) { return true; } return false; } bool Vertical(point u1,point u2,point v1,point v2)//如果有一条线段垂直,只要另一条线段平行X轴就是0 { if(sign(u1.y-u2.y)==0) { if(sign(v1.x-v2.x)==0) return true; } else if(sign(v1.y-v2.y)==0) { if(sign(u1.x-u2.x)==0) return true; } return false; } bool Parallel(point u1,point u2,point v1,point v2)//其实坐到后面发现,两条线段任意一条平行X轴都是0 { if((sign(u1.y-u2.y)==0)||(sign(v1.y-v2.y)==0)) return true; return false; } double slope(point u,point v)//斜率 { if((sign(v.x-u.x)==0)&&(sign(v.y-u.y)==0))//如果交点和最上面的点重合那么就0了 { return INF; } if(sign(v.x-u.x)==0) { return inf; } return (v.y-u.y)/(v.x-u.x); } int main() { int T; int n,m,i,j; int num1,num2; point u1,u2,v1,v2; double d1,d2,k1,k2,h,l,K,B; double area,maxn1,maxn2; point res,a,b,c; cin>>T; while(T--) { cin>>u1.x>>u1.y>>u2.x>>u2.y; cin>>v1.x>>v1.y>>v2.x>>v2.y; p[0]=u1; p[1]=u2; p[2]=v1; p[3]=v2; h=0; l=0; area=0; maxn1=-99999; maxn2=-99999; if(IsIntersected(u1,u2,v1,v2))//是否相交 { if(Same(u1,u2,v1,v2)) { //cout<<"00"<<endl; cout<<"0.00"<<endl; continue; } if(Vertical(u1,u2,v1,v2)) { //cout<<"22"<<endl; cout<<"0.00"<<endl; continue; } if(Parallel(u1,u2,v1,v2)) { //cout<<"33"<<endl; cout<<"0.00"<<endl; continue; } if(sign(slope(u1,u2)-slope(v1,v2))==0) { //cout<<"44"<<endl; cout<<"0.00"<<endl; continue; } res=Intersection(u1,u2,v1,v2); //cout<<"OK!"<<endl; if(res.x==INF&&res.y==INF) { //cout<<"55"<<endl; cout<<"0.00"<<endl; continue; } //cout<<d1<<" "<<d2<<" "<<d3<<" "<<d4<<endl; for(i=0;i<4;i++) { if(maxn1<p[i].y) { maxn1=p[i].y; num1=i; } } for(i=0;i<4;i++) { if(i!=num1) { if(maxn2<p[i].y) { maxn2=p[i].y; num2=i; } } } a.x=p[num1].x; a.y=p[num1].y; b.x=p[num2].x; b.y=p[num2].y; d1=Distance(a,res); d2=Distance(b,res); if((sign(d1-d2)==-1)&&(sign(a.y-b.y)==0))//这里是判断哪条是最上面的点所在的那条直线 swap(a,b); //if((sign(a.x-res.x)==0)) //cout<<a.x<<" "<<a.y<<" "<<b.x<<" "<<b.y<<" "<<res.x<<" "<<res.y<<endl; if((sign(res.x-b.x)==0)&&(sign(res.y-b.y)==0))//如果交点就是第二高的点那么直接是0(不可能装水),极限情况就是交点和第三个点同样高 { //cout<<"11"<<endl; cout<<"0.00"<<endl; continue; } k1=slope(res,a); k2=slope(res,b); //cout<<k1<<" "<<k2<<endl; if(k1!=inf||k2!=inf)//如果斜率都存在 { if((sign(k1)==-1)&&(sign(k2)==-1))//如果斜率小于0 { if(sign(k1-k2)==-1)//只要最高点的那条直线的斜率比次高点的那条直线高 { if(((sign(a.x-b.x)==0)||(sign(a.x-b.x)==-1))&&(sign(a.y-b.y)==1))//遮住了 { //cout<<"1000"<<endl; cout<<"0.00"<<endl; continue; } } } if((sign(k1)==1)&&(sign(k2)==1)) { if(sign(k1-k2)==1)//只要最高点的那条直线的斜率比次高点的那条直线高 { if(((sign(a.x-b.x)==0)||(sign(a.x-b.x)==1))&&(sign(a.y-b.y)==1))//遮住了 { // cout<<"2000"<<endl; cout<<"0.00"<<endl; continue; } } } } c.y=b.y; K=slope(res,a); if(K==INF) { //cout<<"88"<<endl; cout<<"0.00"<<endl; continue; } if(K==inf) { c.x=res.x; //cout<<"xxx"<<endl; //cout<<res.x<<" "<<res.y<<" "<<c.x<<" "<<c.y<<" "<<b.x<<" "<<b.y<<endl; printf("%.2lf\n",fabs(xmult(res,c,b))/2); continue; } B=a.y-K*a.x; if(sign(B)==0) B=0; //cout<<K<<" "<<B<<endl; if(sign(c.y-B)==0) c.x=0; else c.x=(c.y-B)/K; if(sign(c.x)==0) c.x=0; //cout<<a.x<<" "<<b.x<<" "<<c.x<<endl; //h=b.y-res.y; // l=b.x-c.x; //if(l<0) // l=-l; //area=0.5*l*h; //cout<<"YYY"<<endl; //cout<<res.x<<" "<<res.y<<" "<<c.x<<" "<<c.y<<" "<<b.x<<" "<<b.y<<endl; printf("%.2lf\n",fabs(xmult(res,c,b))/2); } else { //cout<<"NO"<<endl; cout<<"0.00"<<endl; continue; } } } /* 9 样例一: 6259 2664 8292 9080 1244 2972 9097 9680 答案:6162.65 样例二: 0 1 1 0 1 0 2 1 答案:1.00 样例三: 0 1 2 1 1 0 1 2 答案:0.00 样例四: 0 0 10 10 0 0 9 8 答案:0.00 样例五: 0 0 10 10 0 0 8 9 答案:4.50 样例六: 0.9 3.1 4 0 0 3 2 2 答案:0.50 样例七: 0 0 0 2 0 0 -3 2 答案:3.00 样例八: 1 1 1 4 0 0 2 3 答案:0.75 样例九: 1 2 1 4 0 0 2 3 答案:0.00 */






















 206
206

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








