Ural1024 (LCM+置换）

                       

1024. Permutations

Time limit: 2.0 second
Memory limit: 64 MB

Background

We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows:

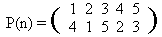
This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc.

What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P( n) is a permutation then P(P( n)) is a permutation as well. In our example (check it by yourself)

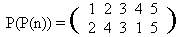
It is natural to denote this permutation by P ²( n) = P(P( n)). In a general form the definition is as follows: P( n) = P ¹( n), P ^k( n) = P(P ^k-1( n)).

Among the permutations there is a very important one — that moves nothing:

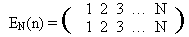
It is clear that for every k the following relation is satisfied: (E _N) ^k = E _N. The following less trivial statement is correct (we won’t prove it here, you may prove it yourself incidentally):

Let P(n) be some permutation of an N elements set. Then there exists a positive integer k, that P^k = E_N.

The least positive integer k such that P ^k = E _N is called an order of the permutation P.

Problem

The problem that your program should solve is formulated now in a very simple manner: “Given a permutation find its order.”

Input

The first line contains the only integer N (1 ≤ N ≤ 1000), that is a number of elements in the set that is rearranged by this permutation. In the second line there are N integers of the range from 1 up to N, separated by a space, that define a permutation — the numbers P(1), P(2),…, P( N).

Output

You should write the order of the permutation. You may consider that an answer shouldn’t exceed 10 ⁹.

Sample

input	output
5 4 1 5 2 3	6

基础数论

题意 :

 就是问能经过多少次置换成为1，2，3，。。n的这样的顺序序列。

置换在离散数学里都学过，很简单，这里找出所有的循环节，然后求出所有循环节的最小公倍数就可以了。

但是在这里，直接求最小公倍数WA,因为有可能溢出。所以要每次算出最大公约数，然后每次计算。

//给出一组排列，问多少次转换后能够得到顺序序列
// 有点像离散数学中的 排列 。。。每次都是针对原始排列进行的，不然会出现 变不到顺序序列的情况。 
//找出最大的循环节  求多个循环节的最小公倍数  
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int a[1005];
int b[1000]; 
bool vis[1005];
int gcd(int a,int b)
{
	if(a<b)swap(a,b);
	
	if(b==0)return a;
	else return gcd(b,a%b);
}
int lcm(int a,int b)
{
	return a/gcd(a,b)*b;
}
int main()
{
//	freopen("q.in","r",stdin);
	int n;
	int i,j;
	memset(vis,0,sizeof(vis));
	scanf("%d",&n);
	for(i=1;i<=n;i++)scanf("%d",&a[i]);
	int mmax=1;
	int len=0;
	for(i=1;i<=n;i++)
	{
		
		if(!vis[i])
		{
			int cnt=1;
			int k=i;
			vis[k]=1;
			while(i!=a[k])
			{
				cnt++;
				k=a[k];
				vis[k]=1;
				
			}
			b[len++]=cnt;
		}
	}

	int tmp=b[0];
	for(i=1;i<len;i++)
	{
		mmax=lcm(tmp,b[i]);
		tmp=mmax;  //  最后应该输出tmp 而不是 mmax  
	} 
	cout<<tmp<<endl; 
/*	  mmax=b[0];
	for(i=1;i<len;i++)   //为何中间加了变量就WA ？？？  
	{
		mmax=lcm(mmax,b[i]);	
	}*/
	cout<<mmax<<endl;

}