zoj 3733 Skycity

           几何。给题意跪了。。。circular truncated cone 这句话是重点，只有读懂这句话才能做出来这道题。。。千万别看图，看了图就哭了。。。在这里给大家说一下题意吧，相信知道题意的话是很容易过的。

           题意：给你一个圆台，即把圆锥的顶去掉，然后给你上表面半径，下表面半径，然后告诉你需要装多少层玻璃，每层高度相同，每层装玻璃的时候保证装出来的是正棱柱，然后还有一个要求就是每个棱柱面的面积不小于s。由于是圆柱，而且知道了一共多少层，那么每层半径就可以直接求出来，还有一个要注意的地方就是正棱柱要完全包含每一层的上底（不知道这样的玻璃是怎么装上的。），每一层直接算正棱柱的最大边数就可以了，因为边数越大，越“贴近”圆，则最终面积肯定最小，根据s可以确定上界，然后就可以直接知道边数了。要求的是使用玻璃面积的最小值。

                             

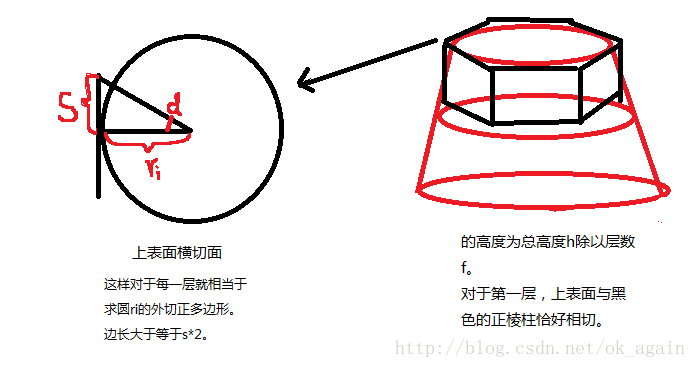
           求圆的外切正多边形，边长大于等于s*2.对于这个问题，我们先求出图示夹角d，然后由于tan(d) = s / ri;所以，d 越大，s越大，边数越少。所以要使得正多边形的边长大于等于s*2，只需要对(2 * PI)   /   (2 * d)   向下取整作为正多边形的边数，必然使得边长大于s（而且此时边数肯定最多）。

#include<cstdio>
#include<cmath>

using namespace std;
const double PI = acos(-1.0);
double R, r, h, f, s;///R：圆台下表面半径。  r：圆台上表面半径。   h：圆台高度。    f：最终玻璃的层数。   s：每块玻璃的最小面积。
int main()
{
    double ans, d, ri, ad;
    while(scanf("%lf%lf%lf%lf%lf", &R, &r, &h, &f, &s) != EOF)
    {
        ans = 0;ad = (R - r) / f;ri = r;
        s = s / 2 / (h / f);///h / f是每层圆台的高度，即玻璃的高度。最小面积s除以每层高度，再除以2，即为图示s。
        for(int i = 0; i < f; i ++)
        {
            d = atan(s / ri);///如图中d。
            int tmp = PI / d;///向下取整。
            ans += tmp * ri * tan(PI / tmp) * 2.0;
            ri += ad;
        }
        printf("%.3lf\n", ans * h / f);
    }
}