Codeforces Round #362 (Div. 2) D Puzzles

http://blog.csdn.net/libin66/article/details/51918509

链接：戳这里

D. Puzzles

time limit per test1 second

memory limit per test256 megabytes

inputstandard input

outputstandard output

Barney lives in country USC (United States of Charzeh). USC has n cities numbered from 1 through n and n - 1 roads between them. Cities and roads of USC form a rooted tree (Barney's not sure why it is rooted). Root of the tree is the city number 1. Thus if one will start his journey from city 1, he can visit any city he wants by following roads.

Some girl has stolen Barney's heart, and Barney wants to find her. He starts looking for in the root of the tree and (since he is Barney Stinson not a random guy), he uses a random DFS to search in the cities. A pseudo code of this algorithm is as follows:


let starting_time be an array of length n
current_time = 0
dfs(v):
current_time = current_time + 1
starting_time[v] = current_time
shuffle children[v] randomly (each permutation with equal possibility)
// children[v] is vector of children cities of city v
for u in children[v]:
dfs(u)
As told before, Barney will start his journey in the root of the tree (equivalent to call dfs(1)).

Now Barney needs to pack a backpack and so he wants to know more about his upcoming journey: for every city i, Barney wants to know the expected value of starting_time[i]. He's a friend of Jon Snow and knows nothing, that's why he asked for your help.

Input
The first line of input contains a single integer n (1 ≤ n ≤ 105) — the number of cities in USC.

The second line contains n - 1 integers p2, p3, ..., pn (1 ≤ pi < i), where pi is the number of the parent city of city number i in the tree, meaning there is a road between cities numbered pi and i in USC.

Output
In the first and only line of output print n numbers, where i-th number is the expected value of starting_time[i].

Your answer for each city will be considered correct if its absolute or relative error does not exceed 10 - 6.

Examples
input
7
1 2 1 1 4 4
output
1.0 4.0 5.0 3.5 4.5 5.0 5.0 
input
12
1 1 2 2 4 4 3 3 1 10 8
output
1.0 5.0 5.5 6.5 7.5 8.0 8.0 7.0 7.5 6.5 7.5 8.0 

题意：

一个树，dfs遍历子树的顺序是随机的。所对应的子树的dfs序也会不同。输出每个节点的dfs序的期望

思路：

分析一颗子树：

当前已知节点1的期望为1.0 ->anw[1]=1.0

需要通过节点1递推出节点2、4、5的期望值

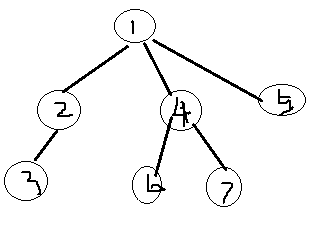
1的儿子分别是2、4、5，那么dfs序所有可能的排列是6种：

1：1-2-4-5  （2、4、5节点的儿子没有写出）

2：1-2-5-4

3：1-4-2-5

4：1-4-5-2

5：1-5-2-4

6：1-5-4-2

计算节点2的期望值得时候，当节点2的前面已经排列了num个点，那么节点2的dfs序就要增加num

所以anw[2]的计算分为两部分，第一部分是：anw[2]=anw[1]+1  （节点1通过1步直接到达儿子2、4、5）

第二部分是：当节点1到达节点2的时候贡献是0，种类分别对应(1、2)

      当先到达节点4后到节点2的时候贡献(size(4)+size(4)+szie(5))，种类分别对应(3、4)

      当先到达节点5后到节点2的时候贡献(size(5)+size(5)+size(4))，种类分别对应(5、6)

而所有的排列对于的概率都是1/6，所以第二部分的贡献就是（0+size(4)*3+size(5)*3）/6 = (size(4)+size(5))/2

仔细推理几颗子树之后：发现anw[v]=anw[u]+1.0+(sz[u]-sz[v]-1)/2.0。

anw[u]+1.0对应第一部分  (sz[u]-sz[v]-1)/2.0 表示的是当前能排在节点v前面的u的儿子的总数  *  0.5

对比1-6的6种排列，任意儿子a、b  ，满足a在b前面的概率是0.5  

代码：

[cpp] view plain copy

1. #include<iostream>  
2. #include<cstdio>  
3. #include<cstring>  
4. #include<algorithm>  
5. #include<string>  
6. #include<vector>  
7. #include <ctime>  
8. #include<queue>  
9. #include<set>  
10. #include<map>  
11. #include<stack>  
12. #include<iomanip>  
13. #include<cmath>  
14. #define mst(ss,b) memset((ss),(b),sizeof(ss))  
15. #define maxn 0x3f3f3f3f  
16. #define MAX 1000100  
17. ///#pragma comment(linker, "/STACK:102400000,102400000")  
18. typedef long long ll;  
19. typedef unsigned long long ull;  
20. #define INF (1ll<<60)-1  
21. using namespace std;  
22. int n;  
23. struct edge{  
24.     int v,next;  
25. }e[500100];  
26. int head[100100],tot=0;  
27. void Add(int u,int v){  
28.     e[tot].v=v;  
29.     e[tot].next=head[u];  
30.     head[u]=tot++;  
31. }  
32. int sz[100100];  
33. void DFS(int u,int fa){  
34.     sz[u]=1;  
35.     for(int i=head[u];i!=-1;i=e[i].next){  
36.         int v=e[i].v;  
37.         if(v==fa) continue;  
38.         DFS(v,u);  
39.         sz[u]+=sz[v];  
40.     }  
41. }  
42. double anw[100100];  
43. void DFS1(int u,int fa){  
44.     for(int i=head[u];i!=-1;i=e[i].next){  
45.         int v=e[i].v;  
46.         if(v==fa) continue;  
47.         anw[v]=anw[u]+1.0+(sz[u]-sz[v]-1)*1.0/2.0;  
48.         DFS1(v,u);  
49.     }  
50. }  
51. int main(){  
52.     mst(head,-1);  
53.     scanf("%d",&n);  
54.     for(int i=2;i<=n;i++){  
55.         int x;  
56.         scanf("%d",&x);  
57.         Add(x,i);  
58.         Add(i,x);  
59.     }  
60.     DFS(1,0);  
61.     anw[1]=1.0;  
62.     DFS1(1,0);  
63.     for(int i=1;i<=n;i++) printf("%.2f ",anw[i]);  
64.     return 0;  
65. }