【leetcode】动态规划_图像处理中动态规划实现断裂的连接-CSDN博客

动态规划(Dynamic Programming)是面试中非常常见的一种算法，可以解决很多复杂问题。

核心算法：

定义状态：dp[i]，一个数组，具体几维根据问题定。
状态转移方程：dp[i] = best(dp[i-1], dp[i-2], ...)。
最优子结构。
递归+记忆化。

动态规划的适用条件

最优子结构性质。一个最优化策略的子策略一定是最优的。
无后向性。可以理解为每个状态都是过去历史状态的完整总结。
子问题的重叠性。这不是DP的必要条件，但是如果不满足，则DP相对其他算法没有优势。因为DP的关键在于解决冗余，存储过程中的各种状态，用空间换时间。

斐波那契数列

f(0) = 0, f(1) = 1, 当n>=2时， f(n) = f(n-1) + f(n-2) 输入n,求f(n)。

比较常见的问题，因此四种做法都能顺利写出来，并分析时间复杂度很重要。

朴素的递推，时间复杂度O(2^n)，空间复杂度?

def fibo(n):
    if n <= 1:
        return n
    return fibo(n-1) + fibo(n-2)

动态规划，时间复杂度O(n)，空间复杂度O(n)

def fibo(n):
    if n <= 1:
        return n
    dp = [0] * (n+1)
    dp[0], dp[1] = 0, 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

改进动态规划，基于循环，时间复杂度O(n)，空间复杂度O(1)

def fibo(n):
    if n <= 1:
        return n
    first_number = 0
    second_number = 1
    for _ in range(n):
        first_number, second_number = second_number, first_number+second_number
    return first_number

零钱兑换1

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

解法：

注：上图是F(0)~F(i-1)

状态方程dp[i]代表总金额为i所对应的最少硬币个数，初始状态dp[0] = 0；

状态转移方程： ; 不存在的为-1。

def coin_change(coins, amount):
    dp = [0xffffff] * (amount + 1)
    dp[0] = 0 # 初始状态，总金额为0，硬币数为0
    for i in range(amount + 1): # 外层循环是总金额
        for coin in coins:
            if i >= coin and dp[i - coin] < dp[i] - 1:
                dp[i] = dp[i - coin] + 1
    if dp[amount] != 0xffffff:
        return dp[amount]
    else:
        return -1

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] = min(dp[x], dp[x - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1

零钱兑换2

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

解法：

状态方程dp[i]代表总金额为i所对应的硬币组合数；

状态转移方程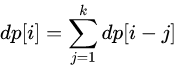：，k为硬币面值个数，注意i要大于等于j。

def change(amount, coins):
    dp = [0] * (amount + 1)
    dp[0] = 1 # 初始状态，总金额为零，组合数为1(所有硬币数都为0)
    for coin in coins: # 外层循环是硬币，用前面面值的硬币组成i的组合数
        for i in range(1, amount + 1): 
            if i >= coin:
                dp[i] = dp[i] + dp[i - coin]
    return dp[amount]

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        dp = [0] * (amount + 1)
        dp[0] = 1
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] += dp[x - coin]
        return dp[amount]

二维矩阵求路径次数(不同路径)

简单版

一个 m x n的二维矩阵，从左上角走到右下角，每次只能往右走或往左走，那么到达右下角总共有多少种走法？

例如，上图是一个7 x 3 的网格。有多少可能的路径？
输入: m = 7, n = 3
输出: 28

解法1：数学排列组合问题。总共有m-1次向下走，n-1次向右走，无论哪种路径都是m+n-2步到达，总的走法有 $C_{m+n-2}^{m-1}$ 种(也就是 $C_{m+n-2}^{n-1}$ )。m=7,n=3, $C_{8}^{2}=\frac{8\times 7}{1\times 2}=28$

解法2：动态规划。到达一个点的路径总数=到达上面一个点的路径总和+到达左边一个点的路径总和。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [0] * m
        for i in range(m):
            dp[i] = [0] * n
        dp[0][0] = 1
        for i in range(0, m):
            for j in range(0, n):
                if i == 0 and j == 0:
                    continue
                dp[i][j] = dp[i-1][j] * (i-1 >= 0) + dp[i][j-1] * (j-1 >= 0)

        return dp[m-1][n-1]

稍微复杂一点

在上面的基础上加上一个条件，矩阵中某些地方不能经过。

只需要在状态转移的时候判断一下，如果当前格点处是不能经过的，那么dp[i][j] = 0；否者，dp[i][j]= dp[i-1][j]*(i-1>=0)+ dp[i][j-1]*(j-1>=0)。

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])
        dp = [0] * m
        for i in range(m):
            dp[i] = [0] * n
        
        if obstacleGrid[0][0] == 0:
            dp[0][0] = 1

        for i in range(0, m):
            for j in range(0, n):
                if i == 0 and j == 0:
                    continue

                if obstacleGrid[i][j] == 0:
                    dp[i][j] = dp[i-1][j] * (i-1 >= 0) + dp[i][j-1] * (j-1 >= 0)

        return dp[m-1][n-1]

最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])

        dp = [0] * m
        for i in range(m):
            dp[i] = [0] * n
        dp[0][0] = grid[0][0]
        for i in range(0, m):
            for j in range(0, n):
                if i == 0 and j == 0:
                    continue
                if i-1 >= 0:
                    temp1 = dp[i-1][j]
                else:
                    temp1 = inf

                if j-1 >= 0:
                    temp2 = dp[i][j-1]
                else:
                    temp2 = inf

                dp[i][j] = grid[i][j] + min(temp1, temp2)

        return dp[m-1][n-1]

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3:

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。

最长公共子序列（lcs）是一道二维动态规划问题，难点在于有两个变量i,j在同时变化，不好理解与思考状态转移方程。
解决方法，思考时，把二维想成一维，即固定text1的i，让j去text1[:i]&text2中找最长公共子序列。
text1[i]=text2[j]时，dp[i][j]=dp[i-1][j-1]+1
text1[i]!=text2[j]时，就要比较最大值是在text1[:i]中，还是text[:i-1]中，dp[i][j]=max(dp[i-1][j],dp[i][j-1])

状态转移方程：
时间复杂度：O(m*n)，两个循环
空间复杂度：O(m*n)，dp是(m,n)大小

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        n,m = len(text1),len(text2)
        dp = [[0]*(m+1) for _ in range(n+1)]
        for i in range(1,n+1):
            for j in range(1,m+1):
                if text1[i-1]==text2[j-1]:
                    dp[i][j]=dp[i-1][j-1]+1
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])
        return(dp[n][m])

剪绳子

给你一根长度为n的绳子，请把绳子剪成m段（m, n都是整数，n > 1 并且 m > 1），每段绳子的长度记为k[0], k[1], ... , k[m]。请问它们的乘积可能的最大值是多少？例如，当绳子的长度为8时，我们把它剪成长度为2、3、3的三段，此时得到的乘积最大，是18.

解法一：动态规划。时间复杂度O(n^2)，空间复杂度O(n)。灵活运用动态规划的关键是具备从上到下分析问题，并且从下到上解决问题的能力。

记长度为n的绳子最大乘积为s[n]

从i中截取一块长度为j的绳子，剩余长度i-j的最大乘积为s[i-j]，即最后一段长度为j的方案带来的乘积为j*s[i-j]

class Solution:
    def cuttingRope(self, n: int) -> int:
        # 记长度为n的绳子最大乘积为s[n]，长度1，s[1]=1
        # 从长度i中截取一块长度为j的绳子，剩余长度i-j的最大乘积为s[i-j]，即最后一段长度为j的方案带来的乘积为j*s[i-j]
        s = [1]*(n+1)
        # 长度i从2到n，长度j从1到i-1
        for i in range(2, n+1):
            for j in range(1, i):
                s[i] = max(s[i], j*s[i-j], j*(i-j))
        return s[n]

三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点在这里指的是下标与上一层结点下标相同或者等于上一层结点下标 + 1 的两个结点。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
[4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

解法：

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        n=len(triangle)
        # 从倒数第二行开始
        # 复用triangle的存储空间
        for row in range(n-2,-1,-1):
            for col in range(len(triangle[row])):
                triangle[row][col]+=min(triangle[row+1][col],triangle[row+1][col+1])
        return triangle[0][0]

参考：

动态规划