动态规划概述

在之前的装配线调度和矩阵链乘法的问题上，大体上已经对如何去解决一个动态规划问题的步骤有了一定的了解。但是，对于什么问题可以用动态规划求解，动态规划的问题有什么明显的特征，或许并不是很清晰，所以下文主要简单的讨论动态规划问题的主要要素，并且讨论一种不同的方法，称为备忘录，以充分利用重叠子问题的性质。

最优子结构：
什么是最优子结构？和最长公共子序列问题中所提到的一样，如果一个问题的一个最优解包含了子问题的最优解，那么该问题就具有最优子结构，那么该问题就可能可以使用动态规划的问题求解（当然贪心策略也是有可能的），而动态规划的解决方式就是通过对子问题的最优解来构造问题的一个最优解。
那该怎么寻找最优解？其实有一种共同的模式：
1.问题的一个解可以是做一个选择，做这样的选择可以得到一个或多个有待解决的子问题。例如在最长公共子序列问题中的前缀的选择，或者选择一个下标来分解矩阵链。
2.假设对一个给定的问题，已知的是一个可以导致最优解的选择。不必关心如何确定这个选择，尽管假设是已知的。

3.在已知这个选择后，要确定哪些子问题会随之发生，以及如何最好的描述所得到的的子问题的空间。

4.利用一种‘剪贴’技术，来证明在问题的一个最优解中，使用的子问题的解本身也是最优的。通过假设每一个子问题的解不是最优的，然后导出矛盾，就可以做到这一点。

在描述子问题空间时，可以遵循一条经验规则，就是尽量保持这个空间简单，然后在必要时去扩充。

最优子结构在问题域中以两种方式变化

1）有多少个子问题被使用在原问题的一个最优解中

2）在决定一个最优解中使用哪些子问题时有多少个选择

在装配线调度的问题中，一个最优解只有一个子问题，但是为了确定最优解有两种不同的选择。在矩阵链乘法中，有两个子问题，就是在k处分裂出去的两遍，但是有j-i种不同的选择。

动态规划以自底向上的方式来利用最优子结构，首先找到子问题的最优解，解决子问题，然后再解决原问题。寻找问题的最优解需要在子问题中做出选择，用哪一个子问题来求解问题。问题解决的代价通常是子问题的代价加上选择的代价。

一些细微之处

要注意不能应用最优子结构的时候，就一定不能假设它能够使用。考虑下面两个问题，已知一个有向图G=(V,E)和节点u,v属于V。

无权最短路径：找出一条从u到v的包含最少边数的路径。

无权最长简单路径：找出一条从u到v的包含最多边数的简单路径。

对于无权最短路径来说，的确是具有最优子结构的特征。从u到v的最短无权路线上假设包含的顶点称为w，那么从u到w的路径以及从w到v的路径必然也是最短的，这点可以通过剪贴法证明，假设从u到w有更短的路径，那么将那条路径贴过来可以构成更短的路径，这与假设不符。但对于无权最长简单路径的问题就不是这样了，假设从u到v的最长简单路径中包含节点w，那么从u到w的路径必然不是最长的，因为从u到w可以先到v那里转一圈然后到w，这样的话路线就明显增长了。所以对于最长简单路径来说，不仅没有最优子结构的性质，而且无法通过子问题的解来构造原问题的解。事实上，这个问题是NP完全的，就是无法通过多项式时间内解决。

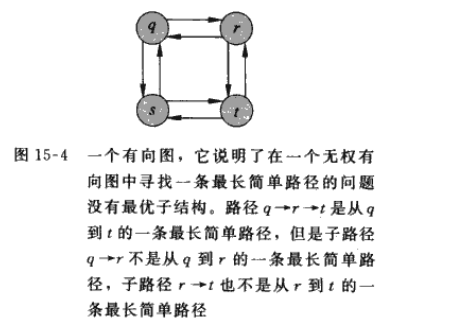
那么为什么最长路径的子结构和最短路径的子结构有如此的不同，简单地说就是因为子问题的独立性，所谓子问题独立，就是一个子问题的求解不会影响到另一个子问题的求解。看下图的例子：要寻找从q到t的最长简单路径有两个子问题，就是找出从q到r以及从r到t的最长简单路径，但对于从q到r，我们可以选择q->s->t->r作为最长的简单路径，但是一旦选择了这样，另一个子问题就会无法解答，因为第二个子问题的资源已经被第一个子问题使用过了，假设再次使用的话合并将会得到一个非简单的路径。

那为什么在寻找最短路径时子问题就是独立的呢？那是因为子问题本来就没有共享资源。如果w在u->v的最短路径上，那么我们就可以通过u->w和w->v的最短路径来产生一条u->v的最短路径。假设某个顶点x同时出现在两条最短路径上，那么可以把第一条最短路径分解成u->x->w，第二条分解成w->x->v，这时候我们发现，直接u->x->v的路径要比u->w->v快两条路径，这与假设相矛盾。

重叠子问题。

动态规划的第二个规则就是要求子问题的规模要很小，也就是说用递归算法可以重复的求解同样的子问题而不是不断的生成新的子问题。当一个递归算法不断调用同一个问题时，我们就称之为最优问题包含重叠子问题。动态规划就是每个子问题求解一次，然后把结果放在一个表中。

重新回顾一下矩阵链乘法的问题，在解决较高行子问题时，要反复查看较低行的子问题。例如，m[3,4]被引用了4次：m[2,4],m[1,4],m[3,5],m[3,6]。如果每一次都被重新计算，那么代价就太大了。为了确定这一点，观察一下直接使用递归式的程序：

将会产生如下的地归树：

这样将会产生指数形式的子问题的数量，但如果使用了重叠子问题的方法，那么只会产生n^2个子问题。

重新构造一个最优解

通常我们是把子问题所作出的选择保存在一个表格中，这样就可以随时查询信息了。

做备忘录

当然，直接使用简单的递归形式也是可以进行动态规划的，备忘录就是一种特殊的动态规划方式，为每个子问题的解在表中记录一个表项。开始时，这个表项有一个特殊值，表示这个地方有待填入数值，当第一次访问这个子问题时，计算这个子问题然后把数据填入表项，以后的访问中只需要简单的访问这个表项而不需要重新进行计算了。这就有点像是标志flag。下面是使用备忘录版本的矩阵链的乘法：