算法导论笔记(2)
分治策略
代入法
两个步骤:
1) 猜测解的形式
2) 用数学归纳法找出解真正有效的常数
递归树法
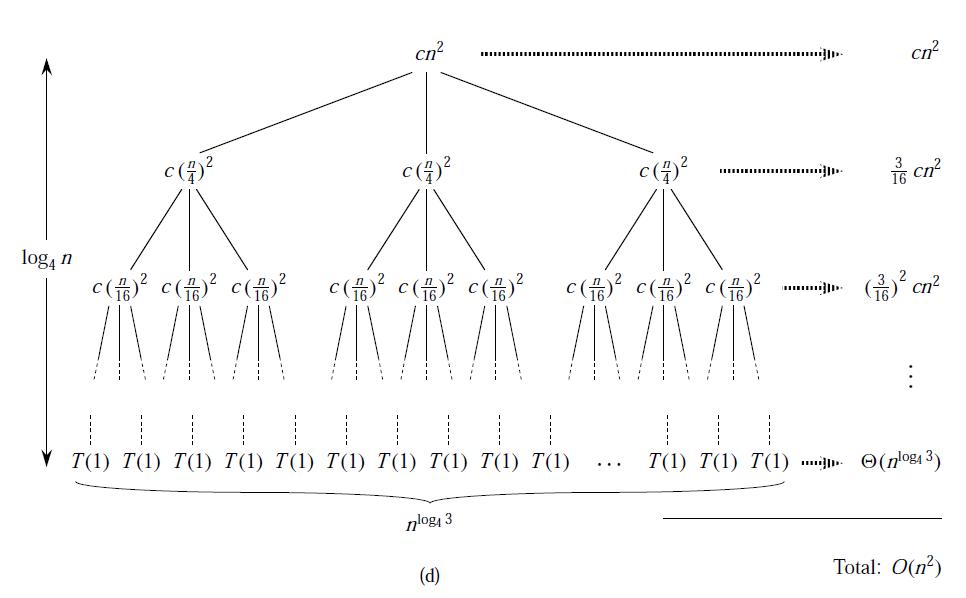
画出一颗递归树来得到好猜测。
在递归树中,每一个结点都代表递归函数调用集合中一个子问题的代价。我们将树中每一层内的代价相加得到一个每层代价的集合,再将每层的代价相加得到递归是所有层次的总代价。
T(n) = 3T(n / 4) + cn^2
主方法
主定理有三种情况,不同的情况有不同的用法
最大子数组
思想
A[low..high]中,可能有三种情况:
完全位于子数组A[low..mid]中
完全位于子数组A[mid..high]中
跨越了中点
所以可以递归的求解
代码
#include <cstdio>
const int MININT = -10000;
int crossArray(int a[],int low,int high){
int mid=(low+high)/2,
sum=0,
left=0,
right=0;
for (int i = mid; i >=low ; i--)
{
sum+=a[i];
if (sum>left)
{
left=sum;
}
}
sum=0;
for (int i = mid+1; i <=high ; ++i)
{
sum+=a[i];
if (sum>right)
{
right=sum;
}
}
return left+right;
}
int maxArray(int a[],int low,int high){
if(low==high){return a[low];}
int mid=(low+high)/2,
leftMax=MININT,
rightMax=MININT,
centerMax=MININT;
leftMax=maxArray(a,low,mid);
rightMax=maxArray(a,mid+1,high);
centerMax=crossArray(a,low,high);
if (leftMax>=rightMax&&leftMax>=centerMax){
return leftMax;
}else if(rightMax>=leftMax&&rightMax>=centerMax){
return rightMax;
}else{
return centerMax;
}
}
int main(int argc, char const *argv[])
{
int a[7]={2,-5,6,12,66,1,-55};
printf("%d\n",maxArray(a,0,6));
return 0;
}
矩阵算法
普通计算
MARTRIX-MULTIPLY(A,B){
n=A.length;
ElemType C[N];
for i=1 to n
for j=1 to n
C^ij=0
for k=1 to n
C^ij=C^ij+A^ik*B^kj;
return C;
}strassen算法
一般矩阵乘法的时间复杂度为n^3=n^{log2^8},Strassen算法则是O(n^{log2^7}) = O(n^{2.807})。但Strassen算法的数值稳定性较差。
一般算法需要八次乘法
r = a * e + b * g ;
s = a * f + b * h ;
t = c * e + d * g;
u = c * f + d * h;
strassen将其变成7次乘法,因为大家都知道乘法比加减法消耗更多,所有时间复杂更高
strassen的处理是:
令:
p1 = a * ( f - h )
p2 = ( a + b ) * h
p3 = ( c +d ) * e
p4 = d * ( g - e )
p5 = ( a + d ) * ( e + h )
p6 = ( b - d ) * ( g + h )
p7 = ( a - c ) * ( e + f )
那么我们可以知道:
r = p5 + p4 + p6 - p2
s = p1 + p2
t = p3 + p4
u = p5 + p1 - p3 - p7
// strassen 算法:将矩阵相乘的复杂度降到O(n^lg7) ~= O(n^2.81)
// 原理是将8次乘法减少到7次的处理
// 现在理论上的最好的算法是O(n^2,367),仅仅是理论上的而已
//
//
// 下面的代码仅仅是简单的实例而已,不必较真哦,呵呵~
// 下面的空间可以优化的,此处就不麻烦了~
#include <stdio.h>
#define N 10
//matrix + matrix
void plus( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = r[i][j] + s[i][j];
}
}
}
//matrix - matrix
void minus( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = r[i][j] - s[i][j];
}
}
}
//matrix * matrix
void mul( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j, k;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = 0;
for( k = 0; k < N / 2; k++ )
{
t[i][j] += r[i][k] * s[k][j];
}
}
}
}
int main()
{
int i, j, k;
int mat[N][N];
int m1[N][N];
int m2[N][N];
int a[N/2][N/2],b[N/2][N/2],c[N/2][N/2],d[N/2][N/2];
int e[N/2][N/2],f[N/2][N/2],g[N/2][N/2],h[N/2][N/2];
int p1[N/2][N/2],p2[N/2][N/2],p3[N/2][N/2],p4[N/2][N/2];
int p5[N/2][N/2],p6[N/2][N/2],p7[N/2][N/2];
int r[N/2][N/2], s[N/2][N/2], t[N/2][N/2], u[N/2][N/2], t1[N/2][N/2], t2[N/2][N/2];
printf("\nInput the first matrix...:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
scanf("%d", &m1[i][j]);
}
}
printf("\nInput the second matrix...:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
scanf("%d", &m2[i][j]);
}
}
// a b c d e f g h
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
a[i][j] = m1[i][j];
b[i][j] = m1[i][j + N / 2];
c[i][j] = m1[i + N / 2][j];
d[i][j] = m1[i + N / 2][j + N / 2];
e[i][j] = m2[i][j];
f[i][j] = m2[i][j + N / 2];
g[i][j] = m2[i + N / 2][j];
h[i][j] = m2[i + N / 2][j + N / 2];
}
}
//p1
minus( r, f, h );
mul( p1, a, r );
//p2
plus( r, a, b );
mul( p2, r, h );
//p3
plus( r, c, d );
mul( p3, r, e );
//p4
minus( r, g, e );
mul( p4, d, r );
//p5
plus( r, a, d );
plus( s, e, f );
mul( p5, r, s );
//p6
minus( r, b, d );
plus( s, g, h );
mul( p6, r, s );
//p7
minus( r, a, c );
plus( s, e, f );
mul( p7, r, s );
//r = p5 + p4 - p2 + p6
plus( t1, p5, p4 );
minus( t2, t1, p2 );
plus( r, t2, p6 );
//s = p1 + p2
plus( s, p1, p2 );
//t = p3 + p4
plus( t, p3, p4 );
//u = p5 + p1 - p3 - p7 = p5 + p1 - ( p3 + p7 )
plus( t1, p5, p1 );
plus( t2, p3, p7 );
minus( u, t1, t2 );
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
mat[i][j] = r[i][j];
mat[i][j + N / 2] = s[i][j];
mat[i + N / 2][j] = t[i][j];
mat[i + N / 2][j + N / 2] = u[i][j];
}
}
printf("\n下面是strassen算法处理结果:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
printf("%d ", mat[i][j]);
}
printf("\n");
}
//下面是朴素算法处理
printf("\n下面是朴素算法处理结果:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
mat[i][j] = 0;
for( k = 0; k < N; k++ )
{
mat[i][j] += m1[i][j] * m2[i][j];
}
}
}
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
printf("%d ", mat[i][j]);
}
printf("\n");
}
return 0;
}
strassen算法转自http://blog.csdn.net/shanshanpt/article/details/8704260










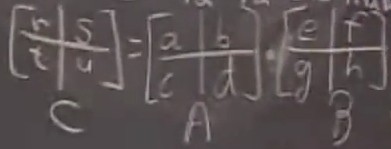














 191
191











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








