二分搜索模板

yiliyo

已于 2022-02-10 19:46:43 修改

阅读量545

点赞数

分类专栏：数据结构与算法文章标签：算法二分法

于 2020-04-10 00:02:11 首次发布

原文链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/er-fen-cha-zhao-suan-fa-xi-jie-xiang-jie-by-labula/

版权

数据结构与算法专栏收录该内容

18 篇文章 1 订阅

订阅专栏

1, 二分搜索，需要保证在升序区间内区间内搜索
2, mid把区间分为左右区间后，判断target在哪个区间进行收缩对应边界：若target在左区间则收缩右边界，若target在右区间则收缩左边界

(1) 若搜索区间是[]，则while (left <= right)， left = mid + 1, right = mid - 1, 即mid把每一次的搜索区间划分为[left, mid - 1] 和[mid + 1, right)。终止循环时left = right + 1。

(2) 若搜索区间是[)，则while (left < right)， left = mid + 1, right = mid, 即 mid 把每一次的搜索区间划分为[left, mid) 和[mid + 1, right)。终止循环时left = right。

3,入参数组nums类型记着用const引用类型，来避免拷贝。

转载自公众号labuladong的力扣题解：

我写了首诗，让你闭着眼睛也能写对二分搜索 :: labuladong的算法小抄

二分查找场景：寻找一个数、寻找左侧边界、寻找右侧边界。

利用左闭右闭区间[left, right]进行搜索，而不是左闭右开。优点：模板代码循环条件统一。缺点：与标准库upper_bound，lower_bound返回结果不一致。

模板代码：

寻找一个数

int binarySearch(const vector<int> &nums, int target) {
    if (nums.size() == 0) {
        return -1;
    }
    int left = 0; 
    int right = nums.size() - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 继续在区间[mid + 1, right]搜索target
        else if (nums[mid] > target)
            right = mid - 1; // 继续在区间[left, mid - 1]搜索target
    }
    return -1;
}

此算法有什么缺陷？

答：这个算法存在局限性。

比如说给你有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

这样的需求很常见，你也许会说，找到一个 target，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的复杂度了。

我们后续的算法就来讨论这两种二分查找的算法。

寻找左侧边界的二分搜索

法1：

eg: [1, 2, 2, 2, 3, 4] ,target = 2; 模板计算的result = left，本例是1.

while循环结束时，right 和 left 存在以下几种可能：（因为left都是mid + 1，所以left不会左越界。（1）但是当target数值不在数组内范围，大于最大值时会右越界。(2)当target数值处于数组内范围，但在数组内找不到target。while后需对这两种检查）

target在数组内找到，left等于target的左边界索引(相同于std::lower_bound())。right 等于left - 1; 返回

target不在数组内，left等于target右边那个值的索引，因此left可能右越界，永远不会左越界。 right等于 left - 1;

0 1 2 3 4 5 6 end()

输入数组[2, 4, 6, 6, 8, 10, 10]

target = 1 -> right = -1; left = 0;

target = 6 -> right = 1; left = 2;

target = 5 -> right = 1; left = 2;

target = 10 -> right = 4; left = 5;

target = 11 -> right = 6; left = end();

int left_bound(const vector<int> &nums, int target) {
    if (nums.size() == 0) {
        return -1;
    }
    int left = 0;
    int right = nums.size() - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid - 1; // 收缩右侧边界
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    // (1)检查索引left右越界 (2)检查target数值在数组内范围但不相等
    if (left >= nums.size() || nums[left] != target)
        return -1;
    return left;
}

由于 while 的退出条件是 left == right + 1，所以当 target 比 nums 中所有元素都大时，会存在以下情况使得索引越界：

因此，最后返回结果的代码应该检查越界情况：

if (left >= nums.length || nums[left] != target)
return -1;
return left;

法2(更通用)：入参为左闭右开[left, right)区间，是搜索区间，更通用，且非注释部分与std::lower_bound结果相同

    // 入参搜索范围[left, right)及结果均与std::lower_bound相同
    int LowerBound(const vector<int> &nums, int target)
    {
        int left = 0;
        int right = nums.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                right = mid;
            } else if (nums[mid] > target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }
        }
        /* 若求"找target在入参搜索区间[)中的第一个位置，若搜不到返回-1。"则用如下注释中代码
        if (left == nums.size()) {
            return -1;
        }
        return nums[left] == target ? left : -1;
        */

        return left;
    }

寻找右侧边界的二分查找

法1：入参左闭右闭

eg: [1, 2, 2, 2, 3, 4] ,target = 2; 模板计算的result = right，本例是2.

while循环结束时，right 和 left 存在以下几种可能：（因为right都是mid - 1，所以right不会右越界。（1）但是当target数值不在数组内范围，小于最小值时会左越界。(2)当target数值处于数组内范围，但在数组内找不到target。while后需对这两种检查）

target在数组内找到，right等于target的右边界索引(不同于std::upper_bound())。left 等于right + 1; 返回right

target不在数组内，right等于target左边那个值的索引，因此right可能左越界，永远不会右越界。 left等于 right + 1; 处理完越界后，返回right

0 1 2 3 4 5 6 end()

输入数组[2, 4, 6, 6, 8, 10, 10]

target = 1 -> right = -1; left = 0;

target = 6 -> right = 3; left = 4;

target = 5 -> right = 1; left = 2;

target = 10 -> right = 6; left = end();

target = 11 -> right = 6; left = end();

int right_bound(const vector<int> &nums, int target) {
    if (nums.size() == 0) {
        return -1;
    }
    int left = 0;
    int right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 收缩左侧边界
            left = mid + 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    // (1)检查索引right左越界 (2)检查target数值在数组内范围但不相等
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

当 target 比所有元素都小时，right 会被减到 -1，所以需要在最后防止越界：

法2(更通用)：入参为左闭右开[left, right)区间，是搜索区间，更通用，且非注释部分与std::upper_bound结果相同

    // 入参搜索范围[left, right)及结果均与std::upper_bound相同
    int UpperBound(const vector<int> &nums, int target)
    {
        int left = 0;
        int right = nums.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }
        }
        /* 若求"找target在入参搜索区间[)中的最后一个位置，若搜不到返回-1。"则用如下注释中代码
        if (left == 0) {
            return -1;
        }
        return nums[left - 1] == target ? left - 1 : -1; // 终止while时left = right, nums[mid] == target时，left = mid + 1。因此left - 1是等于target的右边界.
        */

        return left;
    }

leetcode33 搜索旋转排序数组：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

思路：

// 1, 二分搜索，需要保证在升序区间内区间内搜索
// 2, mid把区间分为左右区间后，判断target在哪个区间进行收缩对应边界：若target在左区间则收缩右边界，若target在右区间则收缩左边界

mid一定会把当前[left, right]分成两部分，其中一部分是有序的。根据有序的那个部分确定我们如何改变二分搜索的上下界。

细节：1,用mid判断升序区间时，判断条件的=不能少，是严格把[left, right]分为两部分的,满足相等条件的场景是[left, right]区间只有两个数如[3, 1]时,仍要分为两个部分。

2,判断target在升序区间内时，与非mid边界判断时，注意需要等号

对[left, right]，先用mid分为红色的两个部分，每次满足条件的这部分是有序的那部分，两部分中的蓝色是与基础二分相同的边界检查。

(1) mid

(2) [left, mid] -> [left, mid)

(3) [mid+1, right] -> (mid, right]

    // 1, 二分搜索，需要保证在升序区间内区间内搜索
    // 2, mid把区间分为左右区间后，判断target在哪个区间进行收缩对应边界：若target在左区间则收缩右边界，若target在右区间则收缩左边界
    int search1(const vector<int> &nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) {
                return mid;
            }
            // mid把[left, right]分为两个区间[left, mid)、(mid, right]，至少一个是升序区间
            if (nums[mid] >= nums[left]) { // 左区间[left, mid)升序
                if (nums[left] <= target && nums[mid] > target) { // 且target在左区间内, 因此收缩右边界
                    right = mid - 1;
                } else {
                    left = mid + 1; // 否则收缩左边界
                }
            } else { // 右区间(mid, right]升序
                if (nums[mid] < target && nums[right] >= target) { // 且target在右区间内, 因此收缩左边界
                    left = mid + 1;
                } else {
                    right = mid - 1; // 否则收缩右边界
                }
            }
        }
        return -1;
    }

搜索旋转排序数组 II

允许旋转数组中元素重复，结果如何？

// 分析：允许重复元素，则上面nums[mid] >= nums[left]使[left, mid]为递增序列的假设就不成立了，比如：[1, 3, 1, 1, 1]。

// 1, 二分搜索，需要保证在升序区间内区间内搜索

// 2, mid把区间分为左右区间后，判断target在哪个区间进行收缩对应边界：若target在左区间则收缩右边界，若target在右区间则收缩左边界

// 3(1),如果nums[left] <= nums[mid]条件不能确定递增序列，那就把它拆分成两个条件：

// 3(2)若nums[mid] > nums[left]，则区间[left, mid]一定递增

// 3(3)若nums[mid] == nums[left]确定不了，那就left++，往下一步看看[leftnew, right]新空间。(因为已经判断过nums[left]不等于target)

    // 分析：允许重复元素，则上面nums[mid] >= nums[left]使[left, mid]为递增序列的假设就不成立了，比如：[1, 3, 1, 1, 1]。
    // 1, 二分搜索，需要保证在升序区间内区间内搜索
    // 2, mid把区间分为左右区间后，判断target在哪个区间进行收缩对应边界：若target在左区间则收缩右边界，若target在右区间则收缩左边界
    // 3(1),如果nums[left] <= nums[mid]条件不能确定递增序列，那就把它拆分成两个条件：
    // 3(2)若nums[mid] > nums[left]，则区间[left, mid]一定递增
    // 3(3)若nums[mid] == nums[left]确定不了，那就left++，往下一步看看[leftnew, right]新空间。(因为已经判断过nums[left]不等于target)
    bool search(const vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) {
                return true;
            }
            // mid把[left, right]分为两个区间[left, mid)、(mid, right]，至少一个是升序区间
            if (nums[mid] > nums[left]) { // 左区间[left, mid)升序
                if (nums[left] <= target && nums[mid] > target) { // 且target在左区间内, 因此收缩右边界
                    right = mid - 1;
                } else {
                    left = mid + 1; // 否则收缩左边界
                }
            } else if (nums[mid] < nums[left]) { // 右区间(mid, right]升序
                if (nums[mid] < target && nums[right] >= target) { // 且target在右区间内, 因此收缩左边界
                    left = mid + 1;
                } else {
                    right = mid - 1; // 否则收缩右边界
                }
            } else {
                left++;
            }
        }
        return false;
    }

多维数组的二分查找

模板仍是一样的，只是计算mid后，mid对应的value是int value = matrix[mid / n][mid % n];

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1:输入:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 3
输出: true

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if (matrix.size() == 0 || matrix.front().size() == 0) {
            return false;
        }

        int m = matrix.size();
        int n = matrix.front().size();
        int left = 0;
        int right = m * n - 1;

        while (left <= right ) {
            int mid = left + (right - left ) / 2;
            int midValue = matrix[mid / n][mid % n];

            if (midValue == target) {
                return true;
            } else if (midValue < target) {
                left = mid + 1;
            } else if (midValue > target) {
                right = mid - 1;
            }
        }
        return false;
    }
};

上述都是直观上的二分。下面列举几道隐式二分：

875. 爱吃香蕉的珂珂

注意点：

（1）把left设置为min_ele是错的。因为若给的h特别大，时间非常充裕，那么k可以为1，而不是数组中的min_ele。left需设置为1。

（2）即使采用左闭右闭求lower_bound的二分框架，也不需要对最后的left进行修正。因为题目条件piles.length <= H且求curH最大值等于数组大小。因此，最后总会走到第一个分支，对right = mid -1处理，left最大等于初始的right。若没有piles.length <= H这个条件，则在H < piles.length计算结果就是左闭右闭求lower_bound二分框架结果，left最终等于初始的right + 1。

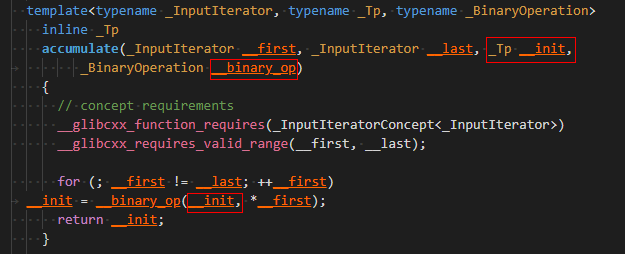
（3）注意accumulate算法传定制的函数对象用法，对init就是第三个参数，并在函数对象内对init进行累加。

class Solution {
public:
    // 法1：求左闭右闭区间的lower_bound
    int minEatingSpeed(vector<int>& piles, int h) {
        int res = 0;
        // if (h < piles.size()) {
        //     return false;
        // }
        int left = 1;
        int right = *max_element(piles.begin(), piles.end());

        while (left <= right) {
            int mid = left + (right - left) / 2;
            int curH = calcCurH(piles, mid);

            if (curH == h) { // 速度相等，再减速看看
                right = mid - 1;
            } else if (curH > h) { // 速度太小，需要加速
                left = mid + 1;
            } else if (curH < h) { // 速度太大，需要减速
                right = mid - 1;
            }
        }
        // 对left的最后修正? 不需要，因为题目条件piles.length <= H且求curH最大值等于数组大小，因此left最大等于初始的right即max_ele
        // 若没有piles.length <= H条件，若H小于piles.length(实际上逻辑上不通，速度再快也不可能一次吃掉两堆香蕉)，则left最终会等于right+1即max_ele+1

        return left;
    }
    int calcCurH(vector<int>& piles, int k)
    {
        int curH = 0;
        curH = accumulate(piles.begin(), piles.end(), 0, [&](int init, int ele) {
            return init + (ele + k - 1) / k;
        });
        return curH;
    }
};

class Solution1 {
public:
    // 法2：求左闭右开区间的lower_bound
    int minEatingSpeed(vector<int>& piles, int h) {
        int res = 0;
        // if (h < piles.size()) {
        //     return false;
        // }
        int left = 1;
        int right = pow(10, 9);
        while (left < right) {
            int mid = left + (right - left) / 2;
            int curH = calcCurH(piles, mid);

            if (curH == h) { // 速度相等，再减速看看
                right = mid;
            } else if (curH > h) { // 速度太小，需要加速
                left = mid + 1;
            } else if (curH < h) { // 速度太大，需要减速
                right = mid;
            }
        }
        // 对left的最后修正? 不需要，因为题目条件piles.length <= H且求curH最大值等于数组大小
        // 若没有piles.length <= H条件，若H小于piles.length(实际上逻辑上不通，速度再快也不可能一次吃掉两堆香蕉)，则left最终会等于初始right即pow(10, 9)

        return left;
    }
    int calcCurH(vector<int>& piles, int k)
    {
        int curH = 0;
        curH = accumulate(piles.begin(), piles.end(), 0, [&](int init, int ele) {
            return init + (ele + k - 1) / k;
        });
        return curH;
    }
};

    int minEatingSpeed(vector<int>& piles, int H) {
        sort(piles.begin(), piles.end());
        int left = 1;
        int right = piles[piles.size() - 1];
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (!calH(piles, H, mid)) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
    bool calH(vector<int>& piles, int H, int k) {
        int sumH = 0;
        for (size_t i = 0; i < piles.size(); i++) {
            sumH += (piles[i] + k - 1) / k;
        }
        return sumH <= H;
    }

109. 有序链表转换二叉搜索树（m）--平衡二叉搜索树

见：https://blog.csdn.net/u011764940/article/details/119892837

109. 有序链表转换二叉搜索树（m）--平衡二叉搜索树

见：https://blog.csdn.net/u011764940/article/details/119892837

附标准库--二分搜索算法(lower_bound/upper_bound/equal_range)

（1）搜索范围都是[)左闭右开。（与multimap和multiset方法一致）

（2）若所有元素均小于val返回end，若所有元素均大于val返回begin)。与multimap和multiset方法一致

（3）另外，对二分lower_bound/upper_bound/equal_range：若beg >= end，则返回beg。

void testcase3()
{
    int myints[] = {10,20,30,30,20,10,10,20};
    std::vector<int> v(myints,myints+8);           // 10 20 30 30 20 10 10 20

    std::sort (v.begin(), v.end());                // 10 10 10 20 20 20 30 30

    std::vector<int>::iterator low,up;
    low=std::lower_bound (v.begin(), v.end(), 9); //          ^
    up= std::upper_bound (v.begin(), v.end(), 9); //                   ^
    std::cout << "lower_bound at position " << (low- v.begin()) << '\n';
    std::cout << "upper_bound at position " << (up - v.begin()) << '\n';

    low=std::lower_bound (v.begin(), v.end(), 31); //          ^
    up= std::upper_bound (v.begin(), v.end(), 31); //                   ^
    std::cout << "lower_bound at position " << (low- v.begin()) << '\n';
    std::cout << "upper_bound at position " << (up - v.begin()) << '\n';

    int a = 9;
}

result:
lower_bound at position 0
upper_bound at position 0
lower_bound at position 8
upper_bound at position 8

void testcase2()
{
    multimap<int, char> mulMp;
    mulMp.insert(make_pair(1, 'a'));
    mulMp.insert(make_pair(2, 'b'));
    mulMp.insert(make_pair(2, 'c'));
    mulMp.insert(make_pair(3, 'd'));

    auto itLow = mulMp.lower_bound(-1);
    auto itUp = mulMp.lower_bound(-1);
    //multimap lower_bound at position 0
    //multimap lower_bound at position 0
    std::cout << "multimap lower_bound at position " << distance(mulMp.begin(), itLow) << '\n';
    std::cout << "multimap upper_bound at position " << distance(mulMp.begin(), itUp) << '\n';

    itLow = mulMp.lower_bound(4);
    itUp = mulMp.lower_bound(4);
    //multimap lower_bound at position 4
    //multimap lower_bound at position 4
    std::cout << "multimap lower_bound at position " << distance(mulMp.begin(), itLow) << '\n';
    std::cout << "multimap upper_bound at position " << distance(mulMp.begin(), itUp) << '\n';

    int a = 1;
}

LeetBook二分查找专项：

力扣https://leetcode-cn.com/leetbook/detail/binary-search/

yiliyo

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
二分搜索模板

https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/er-fen-cha-zhao-suan-fa-xi-jie-xiang-jie-by-labula/
复制链接

扫一扫