回溯算法解子集、组合、排序

转载labuladong：力扣

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

回溯思想团灭排列、组合、子集问题

labuladong发布于 1 个月前2.4k

今天就来聊三道考察频率高，而且容易让人搞混的算法问题，分别是求子集（subset），求排列（permutation），求组合（combination）。这几个问题都可以用回溯算法解决。

一、子集

问题很简单，输入一个不包含重复数字的数组，要求算法输出这些数字的所有子集。

vector<vector<int>> subsets(vector<int>& nums);

比如输入 nums = [1,2,3]，你的算法应输出 8 个子集，包含空集和本身，顺序可以不同：

[ [],[1],[2],[3],[1,3],[2,3],[1,2],[1,2,3] ]

第一个解法是利用数学归纳的思想：假设我现在知道了规模更小的子问题的结果，如何推导出当前问题的结果呢？

具体来说就是，现在让你求 [1,2,3] 的子集，如果你知道了 [1,2] 的子集，是否可以推导出 [1,2,3] 的子集呢？先把 [1,2] 的子集写出来瞅瞅：

[ [],[1],[2],[1,2] ]

你会发现这样一个规律：

subset([1,2,3]) - subset([1,2])

= [3],[1,3],[2,3],[1,2,3]

而这个结果，就是把 sebset([1,2]) 的结果中每个集合再添加上 3。

换句话说，如果 A = subset([1,2]) ，那么：

subset([1,2,3])

= A + [A[i].add(3) for i = 1..len(A)]

这就是一个典型的递归结构嘛，[1,2,3] 的子集可以由 [1,2] 追加得出，[1,2] 的子集可以由 [1] 追加得出，base case 显然就是当输入集合为空集时，输出子集也就是一个空集。

翻译成代码就很容易理解了：

vector<vector<int>> subsets(vector<int>& nums) {
    // base case，返回一个空集
    if (nums.empty()) return {{}};
    // 把最后一个元素拿出来
    int n = nums.back();
    nums.pop_back();
    // 先递归算出前面元素的所有子集
    vector<vector<int>> res = subsets(nums);

    int size = res.size();
    for (int i = 0; i < size; i++) {
        // 然后在之前的结果之上追加
        res.push_back(res[i]);
        res.back().push_back(n);
    }
    return res;
}

这个问题的时间复杂度计算比较容易坑人。我们之前说的计算递归算法时间复杂度的方法，是找到递归深度，然后乘以每次递归中迭代的次数。对于这个问题，递归深度显然是 N，但我们发现每次递归 for 循环的迭代次数取决于 res 的长度，并不是固定的。

根据刚才的思路，res 的长度应该是每次递归都翻倍，所以说总的迭代次数应该是 2^N。或者不用这么麻烦，你想想一个大小为 N 的集合的子集总共有几个？2^N 个对吧，所以说至少要对 res 添加 2^N 次元素。

那么算法的时间复杂度就是 O(2^N) 吗？还是不对，2^N 个子集是 push_back 添加进 res 的，所以要考虑 push_back 这个操作的效率：

vector<vector<int>> res = ...
for (int i = 0; i < size; i++) {
    res.push_back(res[i]); // O(N)
    res.back().push_back(n); // O(1)
}

因为 res[i] 也是一个数组呀，push_back 是把 res[i] copy 一份然后添加到数组的最后，所以一次操作的时间是 O(N)。

综上，总的时间复杂度就是 O(N*2^N)，还是比较耗时的。

空间复杂度的话，如果不计算储存返回结果所用的空间的，只需要 O(N) 的递归堆栈空间。如果计算 res 所需的空间，应该是 O(N*2^N)。

第二种通用方法就是回溯算法。旧文回溯算法详解写过回溯算法的模板：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

只要改造回溯算法的模板就行了：

// 思路：子集. 回溯过过程中，记录树上所有出现的节点，因此没有收敛条件，所有path都记录到res

vector<vector<int>> res;

vector<vector<int>> subsets(vector<int>& nums) {
    // 记录走过的路径
    vector<int> track;
    backtrack(nums, 0, track);
    return res;
}

void backtrack(vector<int>& nums, int start, vector<int>& track) {
    // 因为记录树上所有节点, 所以无需收敛条件。这种遍历到最后是只记录叶节点: if (start == sets.size())
    res.push_back(track);
    // 注意 i 从 start 开始递增
    for (int i = start; i < nums.size(); i++) {
        // 做选择
        track.push_back(nums[i]);
        // 回溯
        backtrack(nums, i + 1, track);
        // 撤销选择
        track.pop_back();
    }
}

可以看见，对 res 的更新是一个前序遍历，也就是说，res 就是树上的所有节点：

二、组合

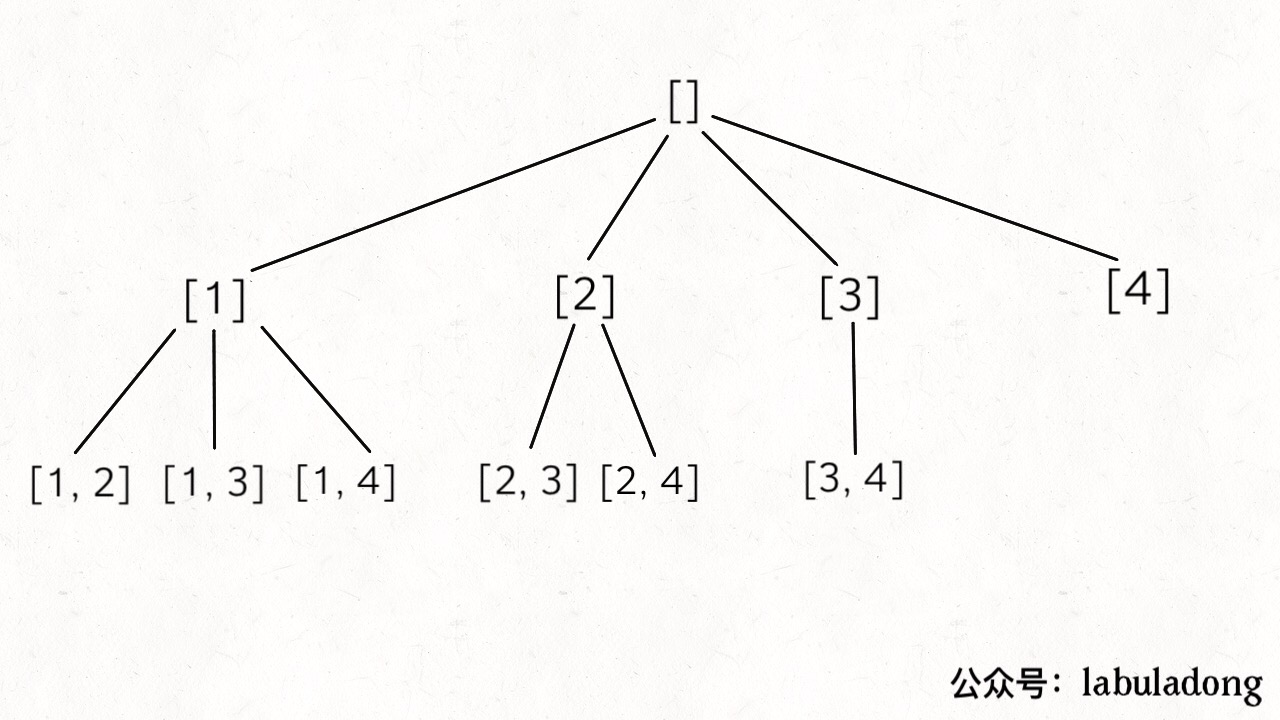
输入两个数字 n, k，算法输出 [1..n] 中 k 个数字的所有组合。

vector<vector<int>> combine(int n, int k);

比如输入 n = 4, k = 2，输出如下结果，顺序无所谓，但是不能包含重复（按照组合的定义，[1,2] 和 [2,1] 也算重复）：

[
[1,2],
[1,3],
[1,4],
[2,3],
[2,4],
[3,4]
]

这就是典型的回溯算法，k 限制了树的高度，n 限制了树的宽度，直接套我们以前讲过的回溯算法模板框架就行了：

vector<vector<int>>res;

vector<vector<int>> combine(int n, int k) {
    if (k <= 0 || n <= 0) return res;
    vector<int> track;
    backtrack(n, k, 1, track);
    return res;
}

void backtrack(int n, int k, int start, vector<int>& track) {
    // 到达树的底部
    if (k == track.size()) {
        res.push_back(track);
        return;
    }
    // 注意 i 从 start 开始递增
    for (int i = start; i <= n; i++) {
        // 做选择
        track.push_back(i);
        backtrack(n, k, i + 1, track);
        // 撤销选择
        track.pop_back();
    }
}

backtrack 函数和计算子集的差不多，区别在于，更新 res 的地方是树的底端。

三、排列

1，一维数组

输入一个不包含重复数字的数组 nums，返回这些数字的全部排列。

vector<vector<int>> permute(vector<int>& nums);

比如说输入数组 [1,2,3]，输出结果应该如下，顺序无所谓，不能有重复：

[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

回溯算法详解中就是拿这个问题来解释回溯模板的。这里又列出这个问题，是将「排列」和「组合」这两个回溯算法的代码拿出来对比。

首先画出回溯树来看一看：

我们当时使用 Java 代码写的解法：

List<List<Integer>> res = new LinkedList<>();

/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;
}

void backtrack(int[] nums, LinkedList<Integer> track) {
    // 触发结束条件
    if (track.size() == nums.length) {
        res.add(new LinkedList(track));
        return;
    }
    
    for (int i = 0; i < nums.length; i++) {
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.removeLast();
    }
}

回溯模板依然没有变，但是根据排列问题和组合问题画出的树来看，排列问题的树比较对称，而组合问题的树越靠右节点越少。

在代码中的体现就是，排列问题每次通过 contains 方法来排除在 track 中已经选择过的数字；而组合问题通过传入一个 start 参数，来排除 start 索引之前的数字。

以上，就是排列组合和子集三个问题的解法，总结一下：

子集问题可以利用数学归纳思想，假设已知一个规模较小的问题的结果，思考如何推导出原问题的结果。也可以用回溯算法，要用 start 参数排除已选择的数字。

组合问题利用的是回溯思想，结果可以表示成树结构，我们只要套用回溯算法模板即可，关键点在于要用一个 start 排除已经选择过的数字。

排列问题是回溯思想，也可以表示成树结构套用算法模板，关键点在于使用 contains 方法排除已经选择的数字，前文有详细分析，这里主要是和组合问题作对比。

排列(输入无重复元素全排列, leetcode 46)回溯另一种解法，不用contains查找是否已选择过，用visit数组(空间换时间)记录候选点是否已在上面的层被选择过：

状态变量为路径track和visit数组两个，在递归前置状态，在递归返回又重置状态恢复现场。

力扣

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> visit(nums.size(), 0);
        vector<int> path;
        BackTrack(nums, visit, path, res);
        return res;
    }
    void BackTrack(vector<int> &nums, vector<int> &visit,
        vector<int> &path, vector<vector<int>> &res)
    {
        if (path.size() == nums.size()) {
            res.push_back(path);
        }

        for (int i = 0; i < nums.size(); i++) {
            if (visit[i] == 1) { // 剪枝：去除上层已选元素
                continue;
            }
            path.push_back(nums[i]);
            visit[i] = 1;
            BackTrack(nums, visit, path, res);
            path.pop_back();
            visit[i] = 0;
        }
    }
};

排列(输入有重复元素，结果不可重复全排列, leetcode 47) 回溯：深搜 + 剪枝：

如输入[1, 1, 2, 1]输出[[1, 1, 1, 2], [1, 1, 2, 1], [1, 2, 1, 1], [2, 1, 1, 1]]

方法一(此方法有缺陷)：

对每层（指兄弟姐妹的结点，即同一个父亲）当有重复元素时进行剪枝，每层初始值赋值为INT_MIN，但是当出现注释中说的情况时结果错。

禁止如下混搭：见重点6

class Solution3 {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> track; // 路径
        sort(nums.begin(), nums.end());
        vector<int> visit(nums.size(), 0);
        size_t length = 0;
        BackTrack(result, length, visit, nums, track);
        return result;
    }

    void BackTrack(vector<vector<int>> &result, size_t length, vector<int> &visit,
        vector<int> &nums, vector<int> &track)
    {
        if (length == nums.size()) {
            result.push_back(track);
            return;
        }

        int levValRec = INT_MIN; // 此处每层记录初始数值是用的INT_MIN，但题目并未规定nums里的元素值不能等于INT_MIN，若nums中有元素有等于此初始值则结果错。
        for (size_t i = 0; i < nums.size(); i++) {
            if (visit[i] == 0 && nums[i] != levValRec) { // 剪枝。每层中重复元素只选第一个元素进行接下来的操作。对其余重复元素无须进行相同的操作，把这些重复元素剪掉。
                levValRec = nums[i];
                visit[i] = 1;
                track.push_back(nums[i]);
                BackTrack(result, length + 1, visit, nums, track);
                visit[i] = 0;
                track.pop_back();
            }
        }
    }
};

应该使用的写法：

class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> track; // 路径
        sort(nums.begin(), nums.end());
        vector<int> visit(nums.size() + 1, 0);
        // size_t length = 0;
        BackTrack(result, visit, nums, track);
        return result;
    }

    void BackTrack(vector<vector<int>> &result, vector<int> &visit,
        vector<int> &nums, vector<int> &track)
    {
        if (track.size() == nums.size()) {
            result.push_back(track);
            return;
        }

        int levValRec = INT_MIN; // 此值选取是否恰当，怎么保证输出nums里的值不等于该值，题目并
                                 // 没有规定，若nums中含有此初始值则结果错。
        for (size_t i = 0; i < nums.size(); i++) {
            if (visit[i] == 0 && nums[i] != levValRec) {
                levValRec = nums[i];
                visit[i] = 1;
                track.push_back(nums[i]);
                BackTrack(result, visit, nums, track);
                visit[i] = 0;
                track.pop_back();
            }
        }
    }
};

方法二：

注：剪枝条件if (i > 0 && nums[i] == nums[i - 1] && visit[i - 1] == 0)中的visit[i - 1] == 0, 写 visit[i - 1] == 0 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择，达到只过滤本层重复元而放过下一层首个重复元效果。

f. 练习题第一题求子集中去除本层重复元时， if (i != start && nums[i] == nums[i - 1])。剪枝条件因为i初始化为start，而条件中的i != start就能保证保留住本层第一个与上层重复元素，而i != start && nums[i] == nums[i - 1]两条件一起来过滤掉本层从第二个开始的重复元。回溯-子集_组合_排序_练习_u011764940的博客-CSDN博客

禁止如下混搭：见重点6

class Solution4 {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> track; // 路径
        sort(nums.begin(), nums.end());
        vector<int> visit(nums.size(), 0);
        size_t length = 0;
        BackTrack(result, length, visit, nums, track);
        return result;
    }

    void BackTrack(vector<vector<int>> &result, size_t length, vector<int> &visit,
        vector<int> &nums, vector<int> &track)
    {
        if (length == nums.size()) {
            result.push_back(track);
            return;
        }

        for (size_t i = 0; i < nums.size(); i++) {
            if (visit[i] == 1) { // 小剪枝，剪掉path在上层中已经选过的数
                continue;
            }
            // 剪枝条件:
            // i > 0, 为了保证 nums[i - 1] 有意义
            // nums[i] == nums[i - 1], 相等时剪枝
            // visit[i - 1] == 0, 写 visit[i - 1] == 0 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
            // 注：写 visit[i - 1] == 1结果也对，但是剪枝点不同，详见: https://leetcode-cn.com/problems/permutations-ii/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liwe-2/
            if (i > 0 && nums[i] == nums[i - 1] && visit[i - 1] == 0) { // 剪枝，
                continue;
            }

            visit[i] = 1;
            track.push_back(nums[i]);
            BackTrack(result, length + 1, visit, nums, track);
            visit[i] = 0;
            track.pop_back();
        }
    }
};

应该使用的写法：

class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> track; // 路径
        sort(nums.begin(), nums.end());
        vector<int> visit(nums.size() + 1, 0);
        // size_t length = 0;
        BackTrack1(result, visit, nums, track);
        return result;
    }

    void BackTrack1(vector<vector<int>> &result, vector<int> &visit,
        vector<int> &nums, vector<int> &track)
    {
        if (track.size() == nums.size()) {
            result.push_back(track);
            return;
        }

        for (size_t i = 0; i < nums.size(); i++) {
            if (visit[i] == 1) {
                continue;
            }
            // 剪枝条件:
            // i > 0, 为了保证 nums[i - 1] 有意义
            // nums[i] == nums[i - 1], 相等时剪枝
            // visit[i - 1] == 0, 写 visit[i - 1] == 0 是因为 nums[i - 1] 在深度优先遍历的过程中             // 刚刚被撤销选择
            // 注：写 visit[i - 1] == 1结果也对，但是剪枝点不同，详见:liweiwei1419的解答
            if (i > 0 && nums[i] == nums[i - 1] && visit[i - 1] == 0) { // 剪枝，
                continue;
            }

            visit[i] = 1;
            track.push_back(nums[i]);
            BackTrack1(result, visit, nums, track);
            visit[i] = 0;
            track.pop_back();
        }
    }
};

下图摘自代码中链接处，是剪枝条件visit[i - 1] == 0时回溯过程。

剪枝条件visit[i - 1] == 1时回溯过程图到原链接处查看，没有及时彻底剪枝。

注：

全排列参考：力扣

2，二维数组

（1）51. N 皇后1(所有可行解)

    // 排列

    // 候选集：对每一行来说皇后可选位置都是[0, 1, ..., n - 1];

    // 记录状态: 用vector<int> c(n, -1);表示n行皇后的位置: 索引为行, 值为列

    // 收敛条件：最后一行有位置能满足皇后定义

    // 剪枝：当前行当前位置不满足皇后定义

  class Solution {
public:
    // 排列
    // 候选集：对每一行来说皇后可选位置都是[0, 1, ..., n - 1];
    // 记录状态: 用vector<int> c(n, -1);表示n行皇后的位置: 索引为行, 值为列
    // 收敛条件：最后一行有位置能满足皇后定义
    // 剪枝：当前行当前位置不满足皇后定义
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<int> c(n, -1);
        int row = 0;
        solveNQueensBackTrack(n, row, c, res);
        return res;
    }
    void solveNQueensBackTrack(int n, int row, vector<int> &c, vector<vector<string>> &res)
    {
        if (row == n) {
            vector<string> path(row, string(row, '.'));
            for (int i = 0; i < row; i++) {
                path[i][c[i]] = 'Q';
            }
            res.push_back(path);
            return;
        }

        for (int i = 0; i < n; i++) {
            if (!IsQueen(row, i, c)) {
                continue;
            }
            c[row] = i;
            solveNQueensBackTrack(n, row + 1, c, res);
            c[row] = -1;
        }
    }

    // 判断满足皇后定义
    bool IsQueen(int row, int val, vector<int> &c)
    {
        for (int i = 0; i < row; i++) {
            // 列
            if (c[i] == val) {
                return false;
            }
            // 斜
            if (row - i == abs(val - c[i])) {
                return false;
            }
        }
        return true;
    }
};

（2）leetcode52 N皇后2(可行解个数)

思路：同上题。在收敛条件：所有行都能找到皇后位置时，私有变量total计数加1。

（3）leetcode37 解数独(一个可行解)

// 思路1：回溯-排列，求一个解（时间复杂度高，每次递归找第一个'.'时存在大量重复动作）

// 收敛条件：最后一行最后一个数满足数独定义

// 候选集: 每个位置都可以从[0, 1, ..., n]选一个数

// 注：1, 需要两层遍历取每一个点, 对每一个点遍历候选集

// 2, 一个解的结果是传入的board本身的部分填充, 候选点直接选入board。

// 3, 几个return的注意和说明，以及需要回溯函数返回bool的原因。回溯（或深搜）里一个可行解的回溯（dfs）函数本身是在满足收敛条件时return并在递归调用处持续return: 若返回void则通过引用带出一个解的结果（哪题是这个场景？返回void的求可行解如何区分收敛的return和遍历完候选集都不满足收敛的return。）; 若返回bool则是题目要求是否有可行解。而本题需要即返回bool又要用引用带出那一个解的结果。因为：(1) 满足收敛条件时需要return，(2) 对某位置点遍历完候选集都不满足数独定义时, 说明该位置点之前的点不满足条件, 需要return, 以对之前的点恢复现场尝试下一候选点。综合(1)(2)的两种return需要进行区分，因此需要返回bool。收敛的return ture需要在递归调用处持续返回true, 遍历候选集过程中不满足数独定义的return false则需要在递归调用后恢复现场并尝试下一候选点。

解法1：
class Solution1 {
public:
    void solveSudoku(vector<vector<char>>& board)
    {
        MysolveSudoku(board);
    }

    bool MysolveSudoku(vector<vector<char>>& board)
    {
        for (size_t i = 0; i < board.size(); i++) {
            for (size_t j = 0; j < board.size(); j++) {
                if (board[i][j] == '.') {
                    for (size_t k = 0; k < board.size(); k++) {
                        board[i][j] = '1' + k;
                        if (IsValid(board, i, j) && MysolveSudoku(board)) {
                            return true;
                        }
                        board[i][j] = '.';
                    }
                    return false;
                }
            }
        }
        return true;
    }

    bool IsValid(vector<vector<char>>& board, size_t x, size_t y)
    {
        // 检查行
        for (size_t i = 0; i < 9; i++) {
            if (i != x && board[i][y] == board[x][y]) {
                return false;
            }
        }
        // 检查列
        for (size_t j = 0; j < 9; j++) {
            if (j != y && board[x][j] == board[x][y]) {
                return false;
            }
        }
        // 检查box
        for (size_t i = 3 * (x / 3); i < 3 * (x / 3 + 1); i++) {
            for (size_t j = 3 * (y / 3); j < 3 * (y / 3 + 1); j++) {
                if ((i != x || j != y) && board[i][j] == board[x][y]) {
                    return false;
                }
            }
        }
        return true;
    }
};

解法2
class Solution2 {
public:
    // 排列
    // 回溯：求一个解
    // 收敛条件：最后一行最后一个数满足数独定义
    // 候选集: 每个位置都可以从[0, 1, ..., n]选一个数
    // 注：1, 需要两层遍历取每一个点, 对每一个点遍历候选集
    // 2, 一个解的结果是传入的board本身的部分填充, 候选点直接选入board。
    // 3, 几个return的注意和说明，以及需要回溯函数返回bool的原因。回溯（或深搜）里一个可行解的回溯（dfs）函数本身是在满足收敛
    // 条件时return并在递归调用处持续return: 若返回void则通过引用带出一个解的结果; 若返回bool则是题目要求是否有可行解。而本题
    // 需要即返回bool又要用引用带出那一个解的结果。因为：(1) 满足收敛条件时需要return，(2) 对某位置点遍历完候选集都不满足数独
    // 定义时, 说明该位置点之前的点不满足条件, 需要return, 以对之前的点恢复现场尝试下一候选点。综合(1)(2)的两种return需要进行
    // 区分，因此需要返回bool。收敛的return ture需要在递归调用处持续返回true, 遍历完候选集不满足数独定义的return false则需要
    // 在递归调用后恢复现场并尝试下一候选点。
    void solveSudoku(vector<vector<char>>& board) {
        if (board.size() == 0) {
            return;
        }
        BackTrack(board);
    }

    bool BackTrack(vector<vector<char>>& board)
    {
        int m = board.size();
        int n = board[0].size();
        // 两层循环遍历对每个位置点
        for (int i = 0; i < m; i++) {  // 每次递归调用找BackTrack'.'的当前位置时存在大量重复动作start
            for (int j = 0; j < n; j++) {
                if (isdigit(board[i][j])) {
                    continue;
                } // 每次递归调用找BackTrack'.'的当前位置时存在大量重复动作end

                // 当前位置点的候选集
                for (int k = 0; k < m; k++) {
                    if (!IsVaid(k + '1', i, j, board)) {
                        continue;
                    }
                    // board选择候选点
                    board[i][j] = k + '1';
                    // // 收敛条件 放置位置1'
                    // if (i == m - 1 && j == n - 1) {
                    //     return true;
                    // }
                    if (BackTrack( board)) {
                        // 已收敛, 持续返回
                        return true;
                    }
                    // board恢复现场
                    board[i][j] = '.';
                }
                // 当前位置遍历完候选集都不符合数独定义, 需return false去把前一个位置给恢复并尝试下一候选点
                return false;
            }
        }
        // 收敛条件 放置位置1
        return true;
    }

    bool IsVaid(char k, int curRow, int curCol, vector<vector<char>>& board)
    {
        // 行
        int row = board.size();
        int col = board[0].size();
        for (int i = 0; i < row; i++) {
            if (board[i][curCol] == k) {
                return false;
            }
        }
        // 列
        for (int i = 0; i < col; i++) {
            if (board[curRow][i] == k) {
                return false;
            }
        }
        // box
        for (int i = (curRow / 3) * 3; i < (curRow / 3) * 3 + 3; i++) {
            for (int j = (curCol / 3) * 3; j < (curCol / 3) * 3 + 3; j++) {
                if (board[i][j] == k) {
                    return false;
                }
            }
        }
        return true;
    }
};

    // 思路2：

    // 整体思路与思路1相同。找唯一一个解，需要在收敛时return，又因为要回溯在候选集未找到满足数独定义时需要return到上一位置恢复现场并尝试下一候选点，因此回溯函数返回bool，收敛时return true, 在候选集未找到合适的候选点时return false.

    // 注：

    // (1)回溯函数开始处直接找到当前board中第一个'.'位置 + 判断收敛。为了避免每次递归都从[0, 0]位置找第一个'.'点，采用传row和col的方式，然后再开始处直接++col处理。

    // (2)剪枝：以三个visit进行hash棋盘已出现数字在各行、列、box是否已被选过，就是备忘录。已经是数独定义了。并不需要再通过专门的遍历进行数独判断。

class Solution {
public:
    // 思路2：
    // 整体思路与思路1相同。找唯一一个解，需要在收敛时return，又因为要回溯在候选集未找到满足数独定义时需要return到上一位置恢复现场并
    // 尝试下一候选点，因此回溯函数返回bool，收敛时return true, 在候选集未找到合适的候选点时return false.
    // 注：
    // (1)回溯函数开始处直接找到当前board中第一个'.'位置 + 判断收敛。为了避免每次递归都从[0, 0]位置找第一个'.'点，采用传row和col的方式，然后再开始处直接++col处理。
    // (2)剪枝：以三个visit进行hash棋盘已出现数字在各行、列、box是否已被选过，就是备忘录。已经是数独定义了。并不需要再通过专门的遍历进行数独判断。

    //行，列，小格内某数字是否已被选过(填过)
    bool visitRow[9][9] = { false };
    bool visitCol[9][9] = { false };
    bool visitBox[9][9] = { false };
    int num = 0;
    void solveSudoku(vector<vector<char>>& board) {
        // 先记录表格中的初始状态
        for(int i = 0; i < 9; i++){
            for(int j = 0; j < 9; j++){
                if(board[i][j] != '.'){
                    visitRow[i][ board[i][j] - '1'] = true;
                    visitCol[j][ board[i][j] - '1'] = true;
                    visitBox[ (i / 3) * 3 + j / 3 ][ board[i][j] - '1'] = true;
                }
            }
        }
        backTrack(board, 0, 0);
    }
    bool backTrack(vector<vector<char>>& board, int row,int col){
        // 找到当前board中第一个'.'位置 + 判断收敛
        while(board[row][col] != '.'){
            if(++col >= 9){
                col = 0;
                row++;
            }
            // 填满了; 收敛条件 
            if(row >= 9)
                return true;
        }
        // 候选集'0' - '9'
        for(int i = 0; i < 9; i++){
            int boxIndex = (row / 3) * 3 + col / 3;
            //已经填了, 小剪枝
            if(visitRow[row][i] || visitCol[col][i] || visitBox[boxIndex][i])
                continue;
            // 选入
            board[row][col] = i + '1';
            visitRow[row][i] = true;
            visitCol[col][i] = true;
            visitBox[boxIndex][i] = true;
            if(backTrack(board, row, col)){
                return true;
            }
            else{
                //最后无法填满, 恢复现场
                board[row][col] = '.';
                visitRow[row][i] = false;
                visitCol[col][i] = false;
                visitBox[boxIndex][i] = false;
            }
        }
        return false;
    }
};

（4）LeetCode：490 迷宫问题

见：算法-搜索_u011764940的博客-CSDN博客

法1：BFS

法2：回溯

注：对于在二维数组中是否能从A点到B点题目，BFS和回溯都可以解。

四，子串满足某条件

重点是确定候选集。是通过substr来获取s.substr(start, i - start +1)长度的子串作为候选集的一个元素。且真正的获取子串若放在剪枝之后，性能更优，剪枝用截取子串的索引及长度进行判断剪枝。

1，leetcode131：分割回文串  

补图：

见练习：CSDN

2，leetcode93：复原IP地址 

补图：

见练习：CSDN

五，在字符矩阵中进行字符串匹配

就像BFS解走迷宫问题一样，对每个点的下一点来说是四个方向上的点。

1，leetcode79. 单词搜索

思路：

// 求一个解，因此需要在收敛时持续return, 又要区别恢复现场的return，所以回溯函数返回值类型为bool
// 把首字母找出，以首字母为起点进行深搜
// 候选集:四个方向
// 剪枝:越过了网格边界
// 收敛path == word
注：1，若要用范围for，则一定要用引用，不要用拷贝。

2，(见重点1、重点12)解法二和第六点二叉树回溯一样，遍历候选集时并没有对下一轮四个方向点的值进行直接判断是否满足条件，而是递归到下一轮，在遍历候选集之前进行判断(类似二叉树的左右孩子，递归调用是传的左右孩子指针，要在下一轮里面进行判断，见二叉树递归_u011764940的博客-CSDN博客，113. 路径总和 II )。因此，加入path是在遍历候选集之前进行，恢复现场是在遍历候选集之后。     而解法1是常规的回溯模板，遍历候选集时，若候选点满足条件则选中并递归调用，紧接着恢复现场。

class Solution {
public:
    // bfs ? 回溯
    // 求一个解，因此需要在收敛时持续return
    // 把首字母找出，以首字母为起点进行深搜
    // 候选集:四个方向
    // 剪枝:越过了网格边界
    // 收敛path == word
    bool exist(vector<vector<char>>& board, string word) {
        struct timeval time1;
        gettimeofday(&time1, nullptr);
        set<pair<int, int>> startSet;
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board[0].size(); j++) {
                if (board[i][j] == word[0]) {
                    startSet.insert(pair<int, int>{i, j});
                }
            }
        }
        vector<vector<int>> visit(board.size(), vector<int>(board[0].size(), 0));
        for (auto &node : startSet) {
            visit[node.first][node.second] = 1;
            string path = string("") + word[0];
            int idx = 0;
            if (BackTrack(board, word, node.first, node.second, idx, visit)) {
                return true;
            }
            visit[node.first][node.second] = 0;
        }
        return false;
    }

    bool BackTrack(vector<vector<char>>& board, string &word,
        int preRow, int preCol, int idx, vector<vector<int>> &visit)
    {
        if (idx == word.size() - 1) {
            return true;
        }

        // 上下左右
        for (auto &curDirect : direct) {
            int curRow = preRow + curDirect[0];
            int curCol = preCol + curDirect[1];
            if (curRow < 0 || curRow >= board.size()) {
                continue;
            }
            if (curCol < 0 || curCol >= board[0].size()) {
                continue;
            }
            if (visit[curRow][curCol] == 1) {
                continue;
            }

            if (board[curRow][curCol] != word[idx + 1]) {
                continue;
            }
            visit[curRow][curCol] = 1;
            if (BackTrack(board, word, curRow, curCol, idx + 1, visit)) {
                return true;
            }
            visit[curRow][curCol] = 0;
        }
        return false;
    }
private:
    vector<vector<int>> direct = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 上下左右
};

class Solution1 {
public:
    bool exist(vector<vector<char>>& board, string word) {
        size_t m = board.size();
        if (m == 0) {
            return false;
        }
        size_t n = board[0].size();
        if (n == 0) {
            return false;
        }

        vector<vector<bool>> visited(m, vector<bool>(n, false));
        vector<vector<int>> directions = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
        for (size_t i = 0; i < m; i++) {
            for (size_t j = 0; j < n; j++) {
                if (dfs(board, 0, i, j, visited, word, directions)) {
                    return true;
                }
            }
        }
        return false;
    }

    bool dfs(vector<vector<char>>& board, int start, int i, int j, vector<vector<bool>>& visited,
             string& word, vector<vector<int>>& directions)
    {
        if (start == word.size()) { // 注：start是从0开始到word.size，总长度是word.size + 1。因此这里的收敛需要return。区别于113. 路径总和 II（收敛时是正处于叶节点，叶节点本身值得恢复需要靠下一轮的终止条件，因此不能在收敛里面return）
            return true;
        }

        if (i < 0 || j < 0 || i >= board.size() || j >= board[0].size()) {
            return false;
        }
        if (visited[i][j] == true) {
            return false;
        }
        if (board[i][j] != word[start]) {
            return false;
        }
        visited[i][j] = true;
        // 法1：循环方式四个方向, 范围for循环auto拷贝, 304ms.
        // for (auto dir : directions) {
        //     if (dfs(board, start + 1, i + dir[0], j + dir[1], visited, word, directions) == true) {
        //         return true;
        //     }
        // }
        // 法2：循环方式四个方向, 范围for循环auto引用, 56ms.
        for (auto& dir : directions) {
            if (dfs(board, start + 1, i + dir[0], j + dir[1], visited, word, directions) == true) {
                return true;
            }
        }
        // 法3：循环方式四个方向，经典for循环 56ms
        // for (size_t k = 0; k < directions.size(); k++) {
        //     if (dfs(board, start + 1, i + directions[k][0], j + directions[k][1], visited, word, directions) == true) {
        //         return true;
        //     }
        // }
        // 法4： 直接穷举方式四个方向，44ms
        // if (dfs(board, start + 1, i + 1, j, visited, word, directions) == true) {
        //     return true;
        // }
        // if (dfs(board, start + 1, i - 1, j, visited, word, directions) == true) {
        //     return true;
        // }
        // if (dfs(board, start + 1, i, j - 1, visited, word, directions) == true) {
        //     return true;
        // }
        // if (dfs(board, start + 1, i, j + 1, visited, word, directions) == true) {
        //     return true;
        // }
        visited[i][j] = false;

        return false;
    }
};

六，二叉树回溯（重点1、重点12）

二叉树结构特殊性，一个cur节点的候选集是指向左右孩子的指针，并不能直接获取左右孩子的val，所以不能在遍历候选集时把孩子的值加入path，只能在递归调用左右孩子里获取孩子的值。

顺序是先终止条件，再cur加入路径path，然后判断本路径是否收敛（收敛条件一般是本cur已经是叶节点，且满足收敛条件），然后遍历候选集（此时对叶节点递归调用左右孩子，会直接满足终止条件返回），最后恢复现场（恢复现场放在遍历候选集之后，因为恢复现场是恢复的path中记录本次选中的cur的val，而不是cur的左右孩子指针，遍历候选集是遍历cur的左右孩子指针，左右孩子的值在递归调用内记录在path，因此左右孩子递归调用返回后path中最后节点才是本cur的val，对其恢复现场）。

框架是：

void Dfs(TreeNode* root, int gap, vector<int>& path, vector<vector<int>>& result)
{
    // 1, 终止条件
    if (root == nullptr)
        return;
    // 2, 加入路径
    path.push_back(root->val);
    // 3, 收敛条件
    if (root->left == nullptr && root->right == nullptr) {
        if (gap == root->val) {
            result.push_back(path);
        }
    }
    // 4, 遍历候选集
    Dfs(root->left, gap - root->val, path, result);
    Dfs(root->right, gap - root->val, path, result);
    // 5, 恢复现场
    path.pop_back();
}

1，leetcode 113. 路径总和 II

见：二叉树递归_u011764940的博客-CSDN博客

回溯经常需要进行剪枝

剪枝分为在进入候选集循环内剪枝和进入候选集之前剪枝。

进入候选集循环内剪枝：

此时，若符合剪枝条件，需选候选集中下一个元素进行判断，则continue（小剪枝）

leetcode47：全排列 II 

leetcode131：分割回文串  

leetcode51+leetcode52：N皇后 

若符合剪枝条件，需退出当前及之后选候选集，则break（中剪枝）

leetcode93：复原IP地址 

练习：CSDN

进入候选集之前剪枝：

此时，若符合剪枝条件，则return（大剪枝），即递归的收敛条件。

leetcode93：复原IP地址 

进入候选集之前及进入候选集循环后均需剪枝：

进入候选集之前剪枝，则return; 进入候选集循环后剪枝，则continue

leetcode93：复原IP地址 

几个重点：

1，在候选集前就会加入路径path的情况。

     首先路径path中加入的都是每个位置上的值，但由于候选集本身表示的是下一位置时，不能直接获取位置上的值，只能递归调用里得到。因此当前位置上的值先加入path，然后遍历候选集，之后再回溯path中当前位置的值。

注意：若候选集本身不能保证退出递归的情况， 一定要在可选集之外的判断处进行return。如下：

// 单词搜索解法2注：start是从0开始到word.size，总长度是word.size + 1。因此这里的收敛需要return。区别于113. 路径总和 II（收敛时是正处于叶节点，叶节点本身值得恢复需要靠下一轮的终止条件，因此不能在收敛里面return）

   （1）二叉树根节点。leetcode113. 路径总和 II （靠终止条件return，来恢复path中叶节点的cur->val）

   （2）在二维数组中单词搜索。leetcode79. 单词搜索 （见解法2，靠收敛条件return，来恢复path中word的最后一个字母）

2，去重(非剪枝)：在子集、组合中传start参数来缩小候选集范围来去重，在排序中通过visit空间换时间去重。

（1）是否需要visit

回溯-子集、组合：用start进行去重，无需visit结构。
回溯-排列：需visit辅助去重，数据结构就是表示候选集全集的bool，如候选集是数组，则visit也是数组。和path一致。
回溯-N皇后：用C[j]记录path, 用row代表depth, 用isvalid(C, row, j)整体剪枝。能满足去重效果, 无需visit结构辅助去重。
回溯-解数独：数独用内容本身剪枝能起到去重效果, 无需visit结构辅助去重。
回溯-子串满足条件，用start进行去重，无需visit结构。
回溯-二叉树：不会有回路，无需去重。

（2）visit数据结构选择

回溯里中的visit一般是和输入的数据结构一样，值填0/1表示该位置是否已经被选择作为path中一个值。

但是区分于图BFS或DFS中的visit，图BFS或DFS的visit一般定义为map<vetex, bool>，表示该顶点是否被选过，而不是位置。

3，何时先对原始输入排序

(1)，结果集要求有序.
(2)，raw数组中有重复元素，且要求返回所有不重复的结果集。需要先排序后，才能对兄弟节点剪枝。
(3)，combination sum这种求使数字和为 target 的组合，需要先排序。因为剪枝条件是用当前元素与当前target比较大小，排序后才能保证在剩余候选集中第一个大于target时的元素剪枝正确，候选集剩下元素均大于target。leetcode39/leetcode40 回溯-子集_组合_排序_练习_u011764940的博客-CSDN博客

4，剪枝之剪去兄弟分支（只去除本层重复元，保留下层重复元）

（1）若可以找到与所有候选集中元素均不同的数值。则在遍历一层候选集之前用该数值初始化一个变量，然后再比较即可。

对子集、组合、排列均适用，eg：本文排列示例法一，练习题40. 组合总和 II法一

题目的其中一条说明：所有数字（包括目标数）都是正整数。

因此可以选一个负数作为一层开始的初始值。

（2）若找不到到与所所有候选集中元素均不同的数值。

对子集、组合：用start初始化候选集起始元素，用if (i != start && nums[i] == nums[i - 1]) 条件剪枝。eg：练习题子集90. 子集 II、练习题40. 组合总和 II法二

        for (size_t i = start; i < nums.size(); i++) {
            if (i != start && nums[i] == nums[i - 1]) {
                continue;
            }
            track.push_back(nums[i]);
            BackTrack(result, i + 1, nums, track);
            track.pop_back();
        }

对排列：需要用回溯后的状态变量visit[i - 1] == false剪枝。eg：本文排列示例法二。

              (eg[1,1,1,2]，若不加visit[i-1]==0条件，排列会对下一层i=0第一个1是上一层选过的，被去重掉，对第二个1，又满足i>0&&nums[i]==nums[i-1]，所以会被误杀。所以加上visit[i-1]==0只杀掉刚恢复状态（本层前一节点），而会保留下隔层之间的第一个未被选过的值相同的数。 对于子集、组合的候选集i = start，就不存在误杀，因为已经保证start就是对path去重功能，本层第一个与上层相同的值会被保留)

5，求子集、组合回溯的候选集到下一层递归调用时，传递的start值有几种情况：

（1）传索引i + 1。适用于candidates 中的每个元素在每个组合中只能使用一次。eg：本文的上面子集、组合题，及练习题中leetcode40. 组合总和 II

（2）仍然传索引i，而不是i+1。 适用于candidates 中的每个元素可以无限制重复被选取。eg：练习题中 leetcode39. 组合总和。

6，候选集起始点是start还是0，以及收敛条件判断，不要混搭。否则，容易错在回溯细节。

（1）for 以start开始
  递归以(i + 1)进入下一轮
  收敛条件以start  == s.size()判断
（2）for 以start开始
  递归以i进入下一轮
  收敛条件以pathsum = target判断
（3）for 以0开始
  递归中path已经添加候选点
  收敛条件以path.size() == s.size()判断

禁止如下混搭：
for 以0开始，递归禁止以(start + 1)进入下一轮， 收敛条件以start == s.size()。应该直接以path添加候选点，收敛条件以path.size() == s.size()判断。

eg：本文排列中的：排列(输入有重复元素，结果不可重复全排列, leetcode 47)。

7，对字符串子串的回溯，候选集通常是用s.substr确定的。

131. 分割回文串、leetcode93：复原IP地址 

8，对只有一个结果的回溯，且直接修改原始输入，且每次递归候选集都是修改后的数组：满足条件时在递归调用处持续返回，否则恢复现场（回溯函数返回值类型为bool）。

     eg：leetcode37 解数独，只有一个解。见练习题。

    是否有可行解的回溯。那找到一个就可以返回。在递归调用处return返回。一般会以或的方式对本层所有候选集进行递归调用。

     eg：一些二叉树的回溯：leetcode112. 路径总和（隐式恢复现场）

     eg：leetcode79. 单词搜索（半隐式恢复现场）

     对要求输出多个解。则不能在递归调用处返回，需要：(1)继续扩展，直至遍历完.（2）需要用path记录一个可行解，并在收敛条件处加入所有可行解结果集。

9，隐式恢复现场。对于求sum且是问是否有可行解这种，递归调用是sum - selectedNode->val，形参是非引用，那么递归返回到上一层后sum就已经是恢复现场了，不用显示恢复现场。（这种归为尾递归）

      eg：二叉树dfs，leetcode112. 路径总和，递归调用是sum - left->val。（是否有可行解的尾递归）

10，半隐式恢复现场。对于是否有可行解，不需要存储路径，但需要通过start索引进行收敛条件判断。需要记录状态的visit显示恢复现场，对于start形参不是传引用，递归返回上一层时start就是隐式恢复现场。

11，对于在二维数组中是否能从A点到B点题目，BFS和回溯都可以解。

12，区分：是在遍历候选集时选中候选点并恢复现场；还是在遍历候选集前加入path，在遍历候选集后恢复现场。

就看遍历候选集的时候，候选集里面是否是真正所要得到的内容(指剪枝判断或加入path的内容)。是真正所要得到的内容：候选集中获取的是和加入path的是在一个维度，不是真正所要得到内容（候选集里获取到的东西和真正需要的不是一个维度，如一个是索引，一个是索引对应的值，需要在下一轮中才能真正获得索引对应的值）：如 113. 路径总和 II ，真正需要取的是val，而候选集取出的仅仅是cur->left和cur->right，并不是cur->left->val，和cur->right->val，left和right的val的获取需要到下一轮才能得到。 又如本文在字符矩阵中进行字符串匹配解法二，真正需要获取的坐标对应的值，遍历候选集时仅获取四周坐标，并没有获取四周坐标所对应的值。

思考的步骤：

1，是求路径条数，还是路径本身。深搜最常见三个问题：求可行解总数，求一个可行解、求所有可行解，求是否有可行解。

 （1）求路径条数，不需要存储路径。

 （2）求路径本身，则需要path数组存路径。

2，只求一个解，还是求所有解？

 （1）如果只求一个解，那找到一个就可以返回(即注意7)。在递归调用处return返回。

 （2）如果要求所有可行解，找到了一个后，还要继续扩展，在候选集里继续找，在递归调用处return不返回，直到遍历完。

 （3）如果是问是否有可行解。那找到一个就可以返回。在递归调用处return返回。一般会以或的方式对本层所有候选集进行递归调用。

3，如何表示状态？

4，如何扩展状态？

5，终止条件是什么？

6，收敛条件是什么？

7，关于判重。

8，关于加速。

 （1）剪枝。

 （2）缓存。