出处:http://blog.csdn.net/xsolver/article/details/9986931
当研究的温度变化过程伴有相变时,如何计算温度场?比如:连铸过程钢液由液态冷却到固态时,除了释放显热,也会释放潜热,而且通常显热量很大,将相变热忽略不计显然不是明智之举。
没有相变时H=H0+Cp×T,H0为参考温度下的热焓,H为热焓,Cp为热容、T为温度,热量传输控制微分方程如下(不知道字母意义的同志不用看了,随便拷贝过来的公式,包含对流项,这里我们假设速度为0,即没有对流项,纯导热问题):
无相变情形,已做介绍。而根据热焓定义我们知道,无论导热方式传热抑或对流方式传热,都会引起物质焓变,即使物质温度未尝变化,热焓可以更好描述物质内含热量的变化。 有相变时,,将Cp×T的地方用H代替,使用如下控制微分方程:
热焓的计算公式,仅仅适用于固液转变一个相变点的情形:
其中fl为所谓的液相率,一个比较粗糙的计算公式如下(Ts和Tl分别是固相线和液相线温度,话说这个公式是根本不存在的,是个坑,很多人跳进来出不去了;其实热焓与温度关系最简单粗暴的方法是多项式拟合,而不是被吹的神乎其神但华而不实的余弦升降函数,这是后话):
显而易见,热焓是温度的函数,已知某温度值就会知道其对应温度下的热焓值,知道热焓亦可知温度值,两者为一一对应的关系,就像人和身份证ID一样一一对应。
如以一维非稳态无热源导热显示为例,则求解如下微分方程:
根据初始温度可以计算得到方程右边值,即四周向控制体包围节点的传递的热量(W/m3),计算方法同前;方程左边离散后,根据右边计算值可以计算得到下一时刻节点的热焓,根据热焓温度关系公式计算其对应温度值,该温度值作为下一时刻迭代的温度初值和热焓初值,继续迭代计算。显式算法中热焓与温度的相互转换显得十分重要,根据公式可以方便由温度计算得到热焓,然而热焓公式非线性时,根据热焓计算温度场就不那么容易了,根据非线性方程求根得到,我试过Steffensen's Accelerating Convergence (Richard L. Burden & J. Douglas Faires: Numerical Analysis (7th Edition) P89),求解速度很快,适用于导数亦连续函数,而若函数表达式中包含上述液相线的表达式时,求解往往以震荡而失败,如下Demo求解3*x^2+exp(x)=0:
#include "stdafx.h"
#include <IOSTREAM.H>
#include <MATH.H>
#define eps 1E-6f
#define REAL float
REAL Fun(REAL x=0)
{
return 2*log(x)+log(3);
}
REAL fsolve(REAL x=0)
{
REAL root,y,z;
for (int i=0;i<100;i++)
{
y=Fun(x);
z=Fun(y);
REAL divisor=(z+x-2*y);
if (fabs(divisor)<eps)
{
cout<<"Two Small Divisor"<<endl;
return root;
}
root=x-(y-x)*(y-x)/divisor;
cout<<x<<";"<<root<<endl;
if (fabs(root-x)<eps)
{
return root;
}
else
{
x=root;
}
}
return 0;
}
int main(int argc, char* argv[])
{
printf("Hello World!\n");
fsolve(3.5);
return 0;
}对于有多个根的情形,初值选取就必须合理,不然求解得到可能不是想要的情形,如上Demo,初值取3.5和1.1可以得到截然不同的两个正确解,以为该算法不行呢,后证明是自己不行,论证如下:
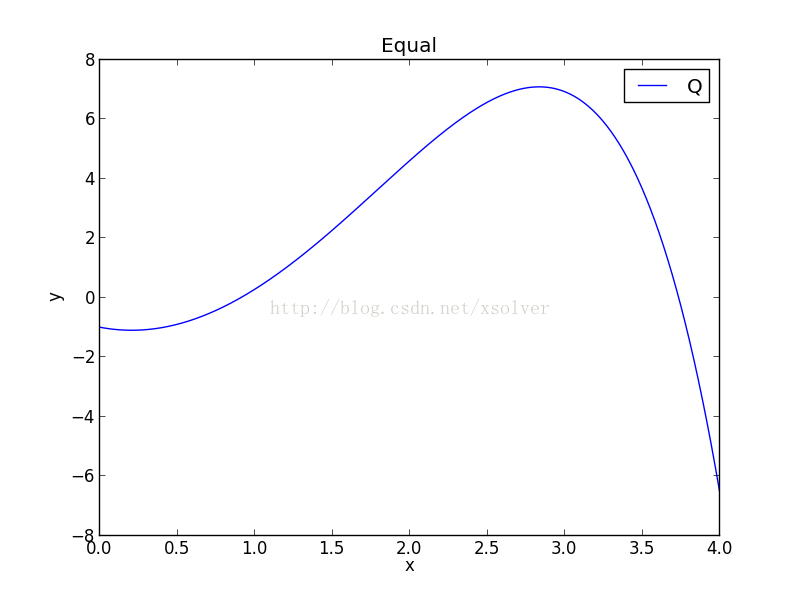
根据如下脚本对该函数绘图:
# -*- coding: utf-8 -*-
"""
Created on Wed Dec 11 09:51:49 2012
@author: Richard Jones Soong
"""
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,4,1000)
plt.plot(x,3*x*x-np.exp(x),label="Q")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Equal")
#plt.ylim(0,0.1)
#Place the Legend to ‘upper left’
plt.legend(loc=1)
plt.show()
热焓方法如何使用隐式求解呢?远比显式的复杂,大家不妨尝试想想。
很多方法可以考虑相变热,如等效比热法、温度回升法。其中温度回升法,物理意义明晰,易于理解。








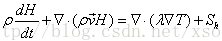
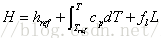
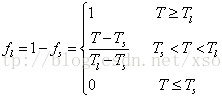
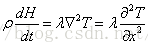














 534
534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








