二分查找法

       二分查找法也叫折半查找，是一种效率比较高的查找方式。前提条件是被查找的数组是有序的。

      主要思想是：

             设查找的数组区间为array[p1, p2]）,元素为从小到大顺序。

             （1）确定该区间的中间位置m

             （2）将查找的值key与array[m]比较。若相等，查找成功返回此位置。

             （3）如果不相等确定新的查找区域，继续二分查找。区域确定如下：

                    如果array[m]>key, 由数组的有序性可知array[m,m+1,……,p2]>key;故新的区间为array[p1,……，m-1]，即p2=m-1;

                    如果array[m]<key, 类似上面查找新的区间为array[m+1,……，p2]，即p1=m+1.

                   然后取新区间的中间值与key比较，可以确定是否查找成功，不成功当前查找区间再缩小一半。重复（2）（3）步骤递归查找即可。如果当数组左边界大于右边界，即p1>p2，则说明数组内没有找到要查找的数，查找失败，位置返回-1.

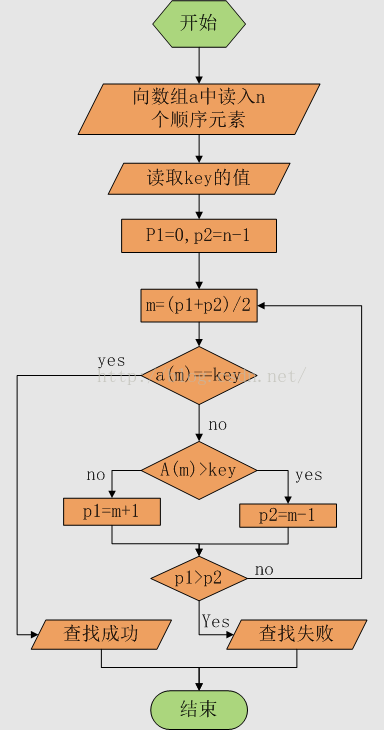
       逻辑顺序图如下：

                                                   

      时间复杂度:O(log2n)。

 java实现的代码如下：

public class BubbleTest
{
    public static int binary(int[] array, int value)
    {
        int low = 0;
        int high = array.length - 1;
        while(low <= high)
        {
            int middle = (low + high) / 2;
            if(value == array[middle])
            {
                return middle;
            }
            if(value > array[middle])
            {
                low = middle + 1;
            }
            if(value < array[middle])
            {
                high = middle - 1;
            }
        }
        return -1;
    }
    public static void main(String[] args)
    {
        int[] a =  { 12, 23, 34, 45, 56, 67, 77, 89, 90 };
        int value = binary(a, 89);
        System.out.println(value);
    }
}