二分图 最大匹配 算法摘记

二分图又称作二部图，是图论中的一种特殊模型。

 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数

可以将 和 当做 着色图：中所有节点为蓝色，中所有节点着绿色，每条边的两个端点的颜色不同，符合图着色问题的要求。

相反，用这样的着色方式对非二分图是行不通的，根据triangle：其中一个顶点着蓝色并且另一个着绿色后，

三角形的第三个顶点与上述具有两个颜色的顶点相连，无法再对其着蓝色或绿色。

给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

特性

• 最小边覆盖集的基数等于最大独立集的基数
• 最大独立集的基数与最大匹配的基数之和，等于顶点数目
• 连通的二部图：
  • 最小顶点覆盖集的基数等于最大匹配的基数

图为二分图当且仅当

• 没有奇数圈
• 点色数为2

二分图匹配

给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

最大匹配: G的所有匹配中边数最多的匹配称为最大匹配.

二分图的最小顶点覆盖 ==== 最大匹配

DAG（无回路有向图）图的最小路径覆盖数 == 节点数 – 最大匹配数

二分图的最大独立集数 = 节点数 – 最大匹配数

在二分图中求最少的点，让每条边都至少和其中的一个点关联，这就是
二分图的“最小顶点覆盖”。

1 一个二分图中的最大匹配数等于这个图中的最小点覆盖数

König定理是一个二分图中很重要的定理，它的意思是，一个二分图中的最大匹配数等于这个图中的最小点覆盖数。如果你还不知道什么是最小点覆盖，我也在这里说一下：

假如选了一个点就相当于覆盖了以它为端点的所有边，你需要选择最少的点来覆盖所有的边。

 

2 最小路径覆盖=最小路径覆盖＝｜G｜－最大匹配数

 在一个N*N的有向图中，路径覆盖就是在图中找一些路经，使之覆盖了图中的所有顶点，
 且任何一个顶点有且只有一条路径与之关联；（如果把这些路径中的每条路径从它的起始点走到它的终点，
 那么恰好可以经过图中的每个顶点一次且仅一次）；

如果不考虑图中存在回路，那么每每条路径就是一个弱连通子集．

由上面可以得出：

 1.一个单独的顶点是一条路径；
 2.如果存在一路径p1,p2,......pk，其中p1 为起点，pk为终点，那么在覆盖图中，顶点p1,p2,......pk不再与其它的
   顶点之间存在有向边．

最小路径覆盖就是找出最小的路径条数，使之成为G的一个路径覆盖．

 路径覆盖与二分图匹配的关系：最小路径覆盖＝｜G｜－最大匹配数；

3 二分图最大独立集=顶点数-二分图最大匹配

独立集：图中任意两个顶点都不相连的顶点集合。

例子：

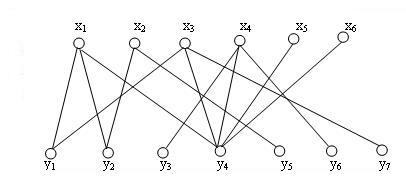
1、起始没有匹配

2、选中第一个x点找第一跟连线 

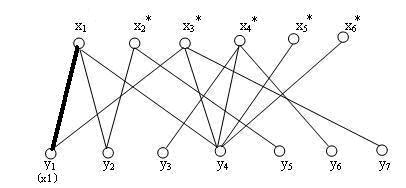
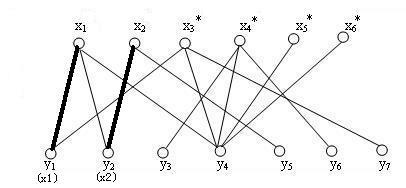
 3、选中第二个点找第二跟连线

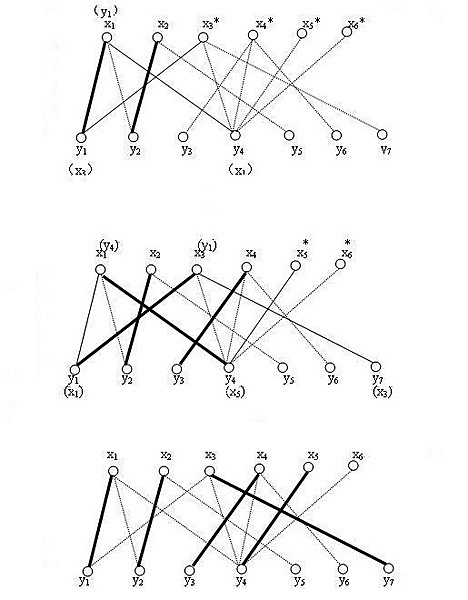
4、发现x3的第一条边x3y1已经被人占了，找出x3出发的的交错路径x3-y1-x1-y4，

把交错路中已在匹配上的边x1y1从匹配中去掉，剩余的边x3y1 x1y4加到匹配中去 

 5、同理加入x4,x5。 
    
    匈牙利算法可以深度有限或者广度优先，刚才的示例是深度优先，即x3找y1,y1已经有匹配，则找交错路。若是广度优先，应为：x3找y1,y1有匹配，x3找y2。 

匈牙利算法的原理为：从当前匹配 (如果没有匹配，则初始匹配为 0)出发，检查每一个未盖点，

然后从它出发寻找可增广路，找到可增广路，则沿着这条可增广路进行扩充，直到不存在可增广路为止。

根据从未盖点出发寻找可增广路搜索的方法，可以分为：

1) DFS 增广

2) BFS增广

3) 多增广路 (Hopcroft-Karp算法 )

http://www.cnblogs.com/kuangbin/archive/2012/08/26/2657446.html

/* **************************************************************************
//二分图匹配（匈牙利算法的DFS实现）
//初始化：g[][]两边顶点的划分情况
//建立g[i][j]表示i->j的有向边就可以了，是左边向右边的匹配
//g没有边相连则初始化为0
//uN是匹配左边的顶点数，vN是匹配右边的顶点数
//调用：res=hungary();输出最大匹配数
//优点：适用于稠密图，DFS找增广路，实现简洁易于理解
//时间复杂度:O(VE)
//***************************************************************************/
//顶点编号从0开始的
const int MAXN=510;
int uN,vN;//u,v数目
int g[MAXN][MAXN];
int linker[MAXN];
bool used[MAXN];
bool dfs(int u)//从左边开始找增广路径
{
    int v;
    for(v=0;v<vN;v++)//这个顶点编号从0开始，若要从1开始需要修改
      if(g[u][v]&&!used[v])
      {
          used[v]=true;
          if(linker[v]==-1||dfs(linker[v]))
          {//找增广路，反向
              linker[v]=u;
              return true;
          }
      }
    return false;//这个不要忘了，经常忘记这句
}
int hungary()
{
    int res=0;
    int u;
    memset(linker,-1,sizeof(linker));
    for(u=0;u<uN;u++)
    {
        memset(used,0,sizeof(used));
        if(dfs(u)) res++;
    }
    return res;
}
//******************************************************************************/

例子：http://www.cnblogs.com/kuangbin/archive/2012/08/19/2646928.html

以上是匈牙利算法的关键代码
其实实现就是一个找增广路径的过程
增广路径 字面意思就是把路径越增越广
DFS从左边起始点开始搜索
1.右边如果没匹配就匹配(link[v]==-1)
2.如果右边匹配过了...就从右边点找左边的匹配点再搜索看是否能增广
以上两种情况都能使匹配边+1

这就是找二分图最大匹配的最简单算法了,代码很短,时间复杂度为O(n^3).

例子 HDOJ 1068 

http://blog.csdn.net/u012605629/article/details/39721759

下面的程序效率很高。是用vector实现邻接表的匈牙利算法。

处理点比较多的效率很高。1500的点都没有问题

/*

HDU 1054

用STL中的vector建立邻接表实现匈牙利算法

效率比较高

 G++  578ms  580K

*/
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<vector>

using namespace std;


//************************************************
const int MAXN=1505;//这个值要超过两边个数的较大者，因为有linker
int linker[MAXN];
bool used[MAXN];
vector<int>map[MAXN];
int uN;
bool dfs(int u)
{
    for(int i=0;i<map[u].size();i++)
    {
        if(!used[map[u][i]])
        {
            used[map[u][i]]=true;
            if(linker[map[u][i]]==-1||dfs(linker[map[u][i]]))
            {
                linker[map[u][i]]=u;
                return true;
            }
        }
    }
    return false;
}

int hungary()

{
    int u;
    int res=0;
    memset(linker,-1,sizeof(linker));
    for(u=0;u<uN;u++)
    {
        memset(used,false,sizeof(used));
        if(dfs(u)) res++;
    }
    return res;
}

//*****************************************************

int main()

{
    int u,k,v;
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=0;i<MAXN;i++)
           map[i].clear();
        for(int i=0;i<n;i++)
        {
           scanf("%d:(%d)",&u,&k);
            while(k--)
            {
                scanf("%d",&v);
                map[u].push_back(v);
                map[v].push_back(u);
            }
        }
        uN=n;
        printf("%d\n",hungary()/2);
    }
    return 0;
}