HDOJ 3473 Minimum Sum_minimum sum csdn-CSDN博客

本文链接：https://blog.csdn.net/ck_boss/article/details/39829857

划分树,统计每层移到左边的数的和.

Minimum Sum

Time Limit: 16000/8000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2959 Accepted Submission(s): 684

Problem Description

You are given N positive integers, denoted as x0, x1 ... xN-1. Then give you some intervals [l, r]. For each interval, you need to find a number x to make

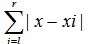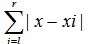as small as possible!

Input

The first line is an integer T (T <= 10), indicating the number of test cases. For each test case, an integer N (1 <= N <= 100,000) comes first. Then comes N positive integers x (1 <= x <= 1,000, 000,000) in the next line. Finally, comes an integer Q (1 <= Q <= 100,000), indicting there are Q queries. Each query consists of two integers l, r (0 <= l <= r < N), meaning the interval you should deal with.

Output

For the k-th test case, first output “Case #k:” in a separate line. Then output Q lines, each line is the minimum value of

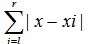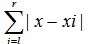. Output a blank line after every test case.

Sample Input

Sample Output

  
  
   
   Case #1:
6
4

Case #2:
0
0

Author

standy

Source

2010 ACM-ICPC Multi-University Training Contest（4）——Host by UESTC

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn=100010;

typedef long long int LL;

int tree[18][maxn];
LL sumL[18][maxn];
int sorted[maxn];
int toleft[18][maxn];

void build(int l,int r,int dep)
{
    if(l==r) return ;
    int mid=(l+r)/2;
    int same=mid-l+1;
    for(int i=l;i<=r;i++)
        if(tree[dep][i]<sorted[mid]) same--;
    int lpos=l,rpos=mid+1;
    for(int i=l;i<=r;i++)
    {
        if(tree[dep][i]<sorted[mid])
        {
            tree[dep+1][lpos++]=tree[dep][i];
            sumL[dep][i]=sumL[dep][i-1]+tree[dep][i];
        }
        else if(tree[dep][i]==sorted[mid]&&same>0)
        {
            tree[dep+1][lpos++]=tree[dep][i];
            sumL[dep][i]=sumL[dep][i-1]+tree[dep][i];
            same--;
        }
        else
        {
            tree[dep+1][rpos++]=tree[dep][i];
            sumL[dep][i]=sumL[dep][i-1];
        }
        toleft[dep][i]=toleft[dep][l-1]+lpos-l;
    }
    build(l,mid,dep+1); build(mid+1,r,dep+1);
}

LL SUMOFLEFT,NUMOFLEFT;

LL query(int L,int R,int l,int r,int dep,int k)
{
    if(l==r) return tree[dep][l];
    int mid=(L+R)/2;
    int cnt=toleft[dep][r]-toleft[dep][l-1];
    if(cnt>=k)
    {
        int newl=L+toleft[dep][l-1]-toleft[dep][L-1];
        int newr=newl+cnt-1;
        return query(L,mid,newl,newr,dep+1,k);
    }
    else
    {
        SUMOFLEFT+=sumL[dep][r]-sumL[dep][l-1];
        NUMOFLEFT+=cnt;

        int newr=r+toleft[dep][R]-toleft[dep][r];
        int newl=newr-(r-l-cnt);
        return query(mid+1,R,newl,newr,dep+1,k-cnt);
    }
}

int n,m;
LL sum[maxn];

int main()
{
    int T_T,cas=1;
    scanf("%d",&T_T);
    while(T_T--)
    {
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",sorted+i);
            tree[0][i]=sorted[i];
            sum[i]=sum[i-1]+sorted[i];
        }
        sort(sorted+1,sorted+1+n);
        build(1,n,0);
        scanf("%d",&m);
        printf("Case #%d:\n",cas++);
        while(m--)
        {
            int l,r,k;
            scanf("%d%d",&l,&r);
            l++; r++;
            k=(l+r)/2-l+1;
            SUMOFLEFT=0;NUMOFLEFT=0;
            LL ave=query(1,n,l,r,0,k);
            printf("%I64d\n",(sum[r]-sum[l-1]-SUMOFLEFT)-SUMOFLEFT+(NUMOFLEFT-(r-l+1-NUMOFLEFT))*ave);
        }
        putchar(10);
    }
    return 0;
}