hdu 4947

GCD Array

Time Limit: 11000/5500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 856    Accepted Submission(s): 209

Problem Description

Teacher Mai finds that many problems about arithmetic function can be reduced to the following problem:

Maintain an array a with index from 1 to l. There are two kinds of operations:

  1. Add v to a _x for every x that gcd(x,n)=d.
  2. Query 

 

Input

There are multiple test cases, terminated by a line "0 0".

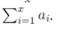
For each test case, the first line contains two integers l,Q(1<=l,Q<=5*10^4), indicating the length of the array and the number of the operations.

In following Q lines, each line indicates an operation, and the format is "1 n d v" or "2 x" (1<=n,d,v<=2*10^5,1<=x<=l).

 

Output

For each case, output "Case #k:" first, where k is the case number counting from 1.

Then output the answer to each query.

 

Sample Input

  
  

   
   6 4
1 4 1 2
2 5
1 3 3 3
2 3
0 0
  
  

 

Sample Output

  
  

   
   Case #1:
6
7
  
  

 

Author

xudyh

 

Source

2014 Multi-University Training Contest 8

题意：首先给你n个数，这n个数刚开始都是0，然后你有两种操作:
1.告诉你y,d,v,然后你要让每个gcd(x,y)=d的a_x加上v。
2.告诉你x，求a1+a2+..+ax的和。

首先根据莫比乌斯反演的两个公式。

以及另一种写法F(n)=E(n|d)f(d)

和f(n)=E(n|d)u(d/n)F(d)

这道题要让gcd(x,y)=d的ax加上v,那么如何运用莫比乌斯反演呢

首先设F(d)为d|gcd(x,y)的对数

f(d)为gcd(x,y)=d的对数

那么发现满足另一种写法的第一个式子

于是f(n)=E(n|d)u(d/n)F(d)

那么f(1)=E(d)u(d)F(d)

由于gcd(x,y)=d(1<=x<=n,y)

可以转化为gcd(x,y)=1(1<=x/d<=n,y/d)

这样f(n)=E(d)u(d)F(d)，即改变函数的上下界

但这样求出的是x/d和y/d的gcd==1的x/d的位置，那么求出后x/d要乘以d才是x

然后发现每次将该位置的数字加上v,即x的倍数加上v,那么可以用树状数组来维护，更新时只让x加上v,x的倍数暂时不变化

对于1-d中多少个数是x的倍数，就是d/x。

那么只要判断查询内有多少个该数字的倍数，然后乘以v就是该数字的增长。

这里光这样还是不能解决这道题，要用到分块思想。考虑x处于[i,p/(p/i)]的范围时，该数字倍数的个数是相同的，那么可以合并同类项。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <string>
#include <vector>
#include <set>
#include <map>
#include <cassert>
using namespace std;

#define CLR(a,b) memset(a,b,sizeof(a))
typedef long long LL;
const int N = 200000+20;
bool check[N];
int mu[N],prime[N];

vector<int> fac[N];
LL f[N];
int l,q;

void Mobius()
{
    CLR(check, 0);
    mu[1] = 1;
    int tot = 0;
    for(int i = 2; i < N ; i++){
        if(!check[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j = 0 ;j < tot; j ++){
            if(i * prime[j] >= N)break;
            check[i * prime[j]] = true;
            if(i % prime[j] == 0){
                mu[i * prime[j]] = 0;
                break;
            }else{
                mu[i * prime[j]] = -mu[i];
            }
        }
    }
    for(int i = 1 ;i < N ; i++){
        for(int j = i ; j < N ; j += i){
            fac[j].push_back(i);
        }
    }
}

inline LL sum(int p){
    LL s = 0;
    while(p > 0){
        s += f[p];
        p -= p & (-p);
    }
    return s;
}

inline void add(int p,int v){
    while(p <= l){
        f[p] += v;
        p += (p) & (-p);
    }
}

void update(int n,int d,int v){
    if(n % d != 0)return;
    
    n = n/d;
    for(int i = 0 ;i < fac[n].size() ; i++){
        int q = fac[n][i];
        add(q * d, v * mu[q]);
    }
}

LL query(int p)
{
    LL ans = 0;
    for(int i = 1,last = i ; i <= p ; i = last + 1){
        last = p/(p/i);
        ans += (LL)(p/i) * (sum(last) - sum(i-1)) ;//分块
    }
    return ans;
}

int main()
{
    Mobius();
    int cas = 0;
    while(~scanf("%d%d",&l,&q)){
        if(l == 0 && q == 0)break;
        CLR(f, 0);
        cas ++;
        printf("Case #%d:\n",cas);
        while(q--){
            int t;
            scanf("%d",&t);
            if(t == 1){
                int n,d,v;
                scanf("%d%d%d",&n,&d,&v);
                update(n, d, v);
            }else{
                int x;
                scanf("%d",&x);
                printf("%I64d\n",query(x));
            }
        }
    }
    return 0;
}