从上往下打印二叉树（Java）

题目：

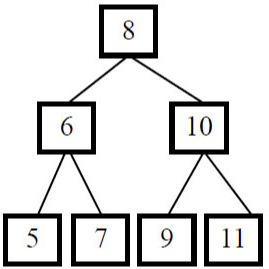
从上往下打印二叉树的每个结点，同一层的结点按照从左到右的顺序打印。例如下图中的二叉树，则依次打印出8、 6、 10、 5、 7、 9、 11。

二叉树结点的定义如下：

struct BinaryTreeNode{
	int m_nValue;
	BinaryTreeNode* m_pLeft;
	BinaryTreeNode* m_pRight;
}

思路：

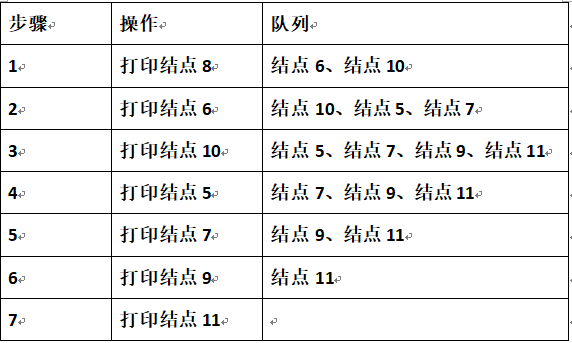
这道题实质是在考查树的遍历算法。只是这种遍历不是我们熟悉的前序（根左右）、中序（左根右）、后序（左右根）遍历。故就需要从树及打印列表分析。分析上图二叉树的层次打印顺序：

通过上图的具体例子的分析，我们可以找到从上到下打印二叉树的规律：每一次打印一个结点的时候，如果该结点有子结点，则把该结点的子结点放到队列的末尾。接下来到队列的头部取出最早进入队列的结点，重复前面的打印操作，直至队列中所有的结点都被打印出来为止。

代码实现：

public class BinaryTreeNode {

	public int data; 
	
	public BinaryTre