Codeforces Round #259 (Div. 2)

A. Little Pony and Crystal Mine

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Twilight Sparkle once got a crystal from the Crystal Mine. A crystal of size n (n is odd; n > 1) is an n × n matrix with a diamond inscribed into it.

You are given an odd integer n. You need to draw a crystal of size n. The diamond cells of the matrix should be represented by character "D". All other cells of the matrix should be represented by character "*". Look at the examples to understand what you need to draw.

Input

The only line contains an integer n (3 ≤ n ≤ 101; n is odd).

Output

Output a crystal of size n.

Sample test(s)

input

3

output

*D*
DDD
*D*

input

5

output

**D**
*DDD*
DDDDD
*DDD*
**D**

input

7

output

***D***
**DDD**
*DDDDD*
DDDDDDD
*DDDDD*
**DDD**
***D***

低端水题：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
int main()
{
    int n;
    while(cin>>n)
    {
        int m=(n+1)/2;
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(j<=m+i-1&&j>=m-i+1)
                {
                    cout<<"D";
                }
                else cout<<"*";
            }
            cout<<endl;
        }
        for(int i=1;i<=n-m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(j<=i||j>=n-i+1)
                {
                    cout<<"*";
                }
                else
                {
                    cout<<"D";
                }
            }
            cout<<endl;
        }
    }
}

B. Little Pony and Sort by Shift

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

One day, Twilight Sparkle is interested in how to sort a sequence of integers a1, a2, ..., an in non-decreasing order. Being a young unicorn, the only operation she can perform is a unit shift. That is, she can move the last element of the sequence to its beginning:

a1, a2, ..., an → an, a1, a2, ..., an - 1.

Help Twilight Sparkle to calculate: what is the minimum number of operations that she needs to sort the sequence?

Input

The first line contains an integer n (2 ≤ n ≤ 105). The second line contains n integer numbers a1, a2, ..., an (1 ≤ ai ≤ 105).

Output

If it's impossible to sort the sequence output -1. Otherwise output the minimum number of operations Twilight Sparkle needs to sort it.

Sample test(s)

input

2
2 1

output

1

input

3
1 3 2

output

-1

input

2
1 2

output

0

还是那句话，对错分离一揽子考虑，a了；

#include<cstdio>
int a[100005];
int main()
{
	int n,b=1,c,x=0,y;
	int flag=0;
	scanf("%d",&n);
	scanf("%d",&a[0]);
	for(int i=1;i<n;i++)
	{
		scanf("%d",&a[i]);
		if(a[i]<a[i-1])
		b=0;
			
	}
	if(a[0]<a[n-1]&&n>2) flag=1;
	for(int i=1;i<n;i++)
	{
		if(a[i]<a[i-1])
		 x++;
		if(x>1)
		{
			flag=1;
			break;
		}
	}
	//printf("%d\n\n",x);
	if(b==1) printf("0\n");
	else if(flag==1) printf("-1\n");
	else
	{
		c=0,y=0;
		for(int i=1;i<n;i++)
		{
			if((a[i]<a[i-1]))
			{
				c=i;
				break;
			}
		}
		printf("%d",n-c);
	}
	
	
	return 0;
}

C. Little Pony and Expected Maximum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.

The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th face contains mdots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.

Input

A single line contains two integers m and n (1 ≤ m, n ≤ 105).

Output

Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10  - 4.

Sample test(s)

input

6 1

output

3.500000000000

input

6 3

output

4.958333333333

input

2 2

output

1.750000000000

Note

Consider the third test example. If you've made two tosses:

1. You can get 1 in the first toss, and 2 in the second. Maximum equals to 2.
2. You can get 1 in the first toss, and 1 in the second. Maximum equals to 1.
3. You can get 2 in the first toss, and 1 in the second. Maximum equals to 2.
4. You can get 2 in the first toss, and 2 in the second. Maximum equals to 2.

The probability of each outcome is 0.25, that is expectation equals to:

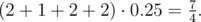
You can read about expectation using the following link: http://en.wikipedia.org/wiki/Expected_value

这题在比赛的时候没思路，觉得就是脑子坏掉了，现在数学思想亟待培养。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdlib>
using namespace std;
int main()
{
	double m;
	double n;
	while(scanf("%lf %lf",&m,&n)!=EOF)
	{
		double sum=0;
		for(double i=1.0;i<=m-1;i++)
		{
			sum+=pow((m-i)/m,n);
		}
		sum=m-sum;
		printf("%.12lf\n",sum);
		
		
	}
	
	
	
	return 0;
}

加油变蓝！！！