最短路径算法（Dijkstra、Floyd）总结

引言

最短路径算法是图算法中比较重要的组成部分，在《算法导论》中有比较详细的阐述和证明。很长时间没在看过图算法的内容，在接触到增强学习后，复习了下A*算法，故对最短路径算法进行一下简单的总结，A*算法将会另外开一篇文章。Dijkstra和Floyd算法是最为经典的两个针对无向图进行最短路径求取的算法，本文先对这两个算法进行回顾和总结。

Dijkstra算法

Dijkstra算法在解决最短路径算法时有一定的局限性，要求图中不能存在负边权重（具体的证明可参考《算法导论》）。个人看来Dijkstra算法应该属于贪心算法的部分，但某些参考书籍把它归入到了动态规划的范围。当然我们不会对这个问题深究，看自己证明好理解吧。Dijkstra是从源点出发，一次求取到其余所有点的最短路径。这也称为单源最短路径。
$\qquad$算法的大致是先从源点$S$出发，选取距离源点距离最短的点$V1$，然后比较从$S$到$V2$的距离$d_{s,v2}$和以$V1$为过渡点再到$V2$的距离$d_{s,v1,v2}$大小。如果前者大于后者，则更新$S$到$V2$的距离为$d_{s,v1,v2}$，否则不改变。然后依次类推计算后面的点，最终得出从$S$到所有点的最短路径。上面说得可能比较抽象，不要急，这只是一个大致阐述，后面你会很清楚的。经过上面的阐述，也看出了一个事实，每次选取的是最小的点，这是贪心的思想，但在求取另外的点时又利用到了之前求取的点，这便又和动态规划相似。现在，我们以一个具体的例子来说明算法的具体求解过程。
如上图，现在我们要求从源点$A$开始求取图中其它点的最短路径。具体过程是：
（1）. 将$A$放入最后的结果中$Ret$；
（2）. 选取与$A$距离最短的点，显然是$C$，更新$A$经过$C$到其它与$C$有直接连接的点的距离，更新的规则上面已经说过，以$B$为例，$A->B$的距离大于$A->C->B$的距离，所以更新$A->B$的距离为5。同时，$A$到$DE$初始是无穷大（图的存储约定），所以更新$A$到$DEF$的距离分别为{6、7}，并加入最后的结果中，$Ret=\{A,C\}$；
（3）. 由于$C$已经被选取，在下一次选择距离$A$最短的点时就不再考虑$C$，那么这次选择显然就是$B$，比较还没加入$Ret$且和$B$直接连接的点$（C、D）$，更新规则和上面一样，最后将$B$加入到$Ret$中，这时$Ret=\{A,C,B\}$;
（4）. 以此类推，选择$D$并更新和$D$直接相连的点，并加入到$Ret$中。
最后$Ret=\{A,C,B,D,E,F\}$,这便是源点$A$到图中所有点的最短路径，例如求$A->E$的最短路径便是$A-C-B-D-E$。简易代码如下（因为手头电脑问题，并没有运行检查正确性）：

const int MAXINT = INT_MAX;        //图中不直接连接的点的权重定义
const int MAXNUM = 6;               //图中的节点数目
int dst[MAXNUM];                    //存放源点到其它点的距离
int prev[MAXNUM];                   //存放路径

int G[MAXNUM][MAXNUM];              //图的邻接矩阵

void Dijstra(int v0)
{
    bool used[MAXNUM];                 // 判断图中节点时候已经被加入最后的结果中，初始为false
    int node_num = MAXNUM;
    for(int i = 1; i<=n; i++)
    {
        dst[i] = G[v0][i];          //从邻接矩阵中获取距离信息
        used[i] = false;
        if( MAXINT == dst[i] )
            prev[i] = -1;
        else
            prev[i] = v0;           // 设置源点直接连接的点的前驱为源点
    }

    dst[v0] = 0;                    // 源点到源点的距离设置为0
    used[v0] = true;                   //标记源点已经被加入最后的结果中

    for(int i = 2; i <= n; i++){
        int mindst = MAXINT;
        int u = v0;
        for(int j = 1; j <= n; j++)          // 选取目前距离矩阵中与源点最短距离的点
        {
            if( (!used[j]) && dst[j] < mindst){
                u = j;
                mindst = dst[j];

            }

            used[u] = true;                    //将该点加入到最后结果中
            for(int j = 1; j <= n; ++j)
            {
                if( (!used[j]) && G[u][j] < MAXINT)
                {
                    if(dst[u]+G[u][j] < dst[j])
                    {
                        dst[j] = dst[u]+G[u][j];    // 更新距离
                        pre[j] = u;                 // 设置前驱
                    }
                }
            }
        }
    }
}

Floyd算法

Dijkstra算法是解决单源最短路径算法，当需要解决图中任意两点的最短路径时，Dijkstra则需要多次计算，而且，当图中存在负的边权重时，Dijkstra则显得无能为力。Floyd算法的提出很好的解决了这一问题，能一次求出任意两点的最短路径，并且边权重可正可负。
$\qquad$Floyd算法的思想是从两点最短路径的可能性思考的，两点之间的最短路径无非有如下几个情况：
（1）. 两点直接到达的距离最短。
（2）. 两点之间通过1个或者1个以上节点连接到达的距离最短。
所以，如果是第一种情况，则可以在邻接矩阵中直接获取。如果是第二种情况，则需要依次判断以每个点为中间点连接起点和终点的最短距离。如果需要中间点的个数大于1，则将问题继续划分为其它终点和起点的问题。例如求AB间的最短距离，对于中间点有C，那么则需要判断$distance(A,B)$与$distance(A,C)+distance(C,B)$的大小，如果还有其它点，则间$distance(A,C)$和$distance(C,B)$按照这种方式继续划分下去，很显然，Floyd算法其实就是一种自顶而低的动态规划。我们先给出代码：

void getGraphicData(){//获取数据  
    ifstream in("data");  
    in>>vertexnum>>edgenum;  //获取节点数和边数
    int from,to;  
    double w;  
    // 初始化邻接矩阵和路径矩阵
    while(in>>from>>to>>w){  
        weight[from][to] = w;  
        path[from][to] = from;
        weight[from][from] = 0; 
        path[from][from] = from;  
        weight[to][to] = 0;  
        path[to][to] = to;  
    }  
}  
void floyd(){  
    for(int k = 0;k < vertexnum;k++)  // 中间点变量
        for(int i= 0;i < vertexnum;i++)  // 起点变量
            for(int j = 0;j < vertexnum;j++){  //终点变量
                    weight[i][j] = min(weight[i][j], weight[i][k] + weight[k][j]);  
                    path[i][j] = path[k][j];  
                }  
            }  
}  
void displaypath(int source,int dest){  // 求取路径
    stack<int> shortpath;  
    int temp = dest;  
    while(temp != source){  
        shortpath.push(temp);  
        temp = path[source][temp];  
    }  
    shortpath.push(source);  
    cout<<"short distance:"<<weight[source][dest]<<endl<<"path:";  
    while(!shortpath.empty()){  
        cout<<shortpath.top()<<" ";  
        shortpath.pop();  
    }  
}  

结合下图：

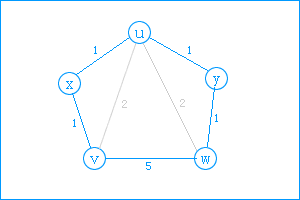
(1). 初始化工作无非就是对图的邻接矩阵就行初始化，直接连接的边为常数权重，非直接连接的边初始化为无穷大，路径矩阵则是对点的前驱进行计算。
(2). 首先确定中间点$k$，例如$k=x$，计算$[u,v]$的最短距离,显然：

$${dist(u,v)=min(dist(u,x)+dist(x,v),dist(u,v))}$$ $dist(u,v)$是邻接矩阵的值（无穷大），所以 $[u,v]$的最短距离目前应该是 $[u->x->v]$。当需要加入更多中间点时，则按照这种方式继续划分下去。在划分过程中比较路径大小，最后得出最小值。
(3). 最后是确立路径，也就是起点和终点之间的中间点。
Floyd算法在实现时有一点需要注意，就是中间点的循环(这里时k)必须在外层，如果放在内层时，有的路径权重不会改变，这会对最后的结果产生错误，说起来比较难懂，可以手动模拟一下，就会发现这个问题。

小结

Dijkstra算法适合于单点的路径就算，而当需要任意两点间的最短路径时，Floyd算法比$V$次Dijkstra算法效率要高，并且当图中存在负权重时，Dijkstra则无能为力。除了这两种算法外，SPFA对于稀疏图的效率比较高，但计算任意两点的最短路径时，Floyd算法的效率依然高于$V$次SPFA计算效率。