什么是“精度”？

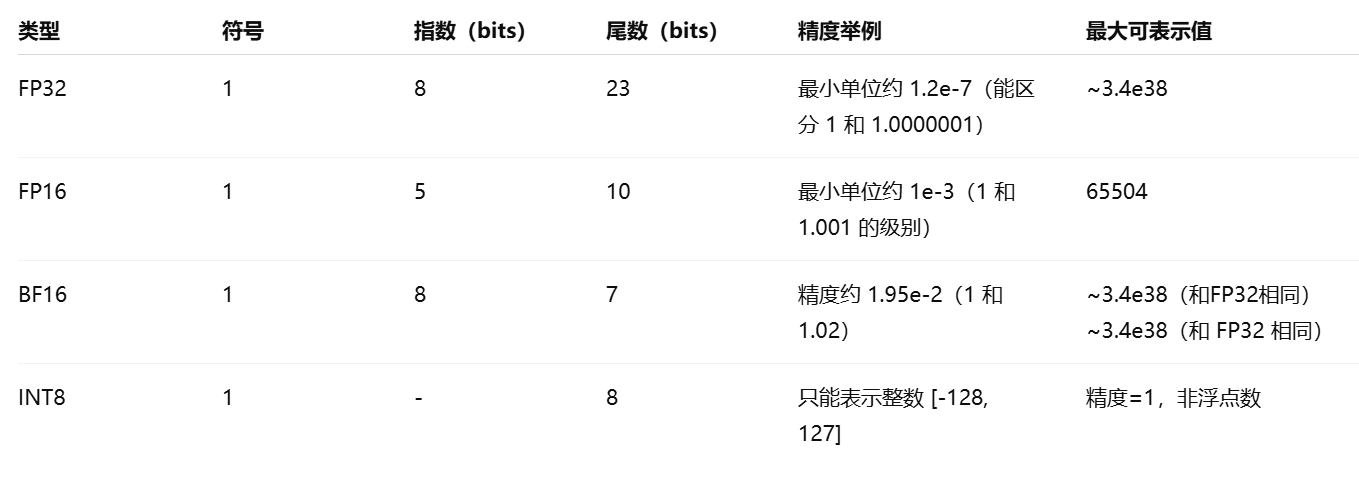
这个表格里 “精度举例”一列不是在讲小数有几位，而是：

举的是“能分辨的最小差值单位”（也叫 machine epsilon / ULP 单位），用于表示数值之间最小可区分的差异，即精度粒度。

---

🧠 什么是“精度”？

这个“精度”的意思是：

两个相邻浮点数之间的最小差值，也可以理解为 该数据类型下，两个不同数字之间的最小可区分单位（resolution）

比如：

• FP32 精度是约 1.2e-7，意味着它能区分 1.0000000 和 1.0000001，但分辨不了 1.0000000001。
• FP16 精度约 1e-3，也就是说 1.000 和 1.001 可以区分，但更细的就不行了。

---

✅ 所以，表格中“精度举例”表达的是：

类型	精度粒度举例（Δ）	能区分的范围
FP32	约 1.2e-7	能区分 1 和 1.0000001
FP16	约 1e-3	能区分 1 和 1.001
BF16	约 1.95e-2（1/2⁷）	能区分 1 和 1.02
INT8	精度为整数 1，只能区分整数	无法区分 1.1 和 1.2 等小数

---

❓是不是没考虑“小数位”？

要分情况：

✅ 浮点数（FP32、FP16、BF16）

这些类型虽然在内部分配了尾数位（小数部分的比特位），但“精度”不是指能表示几位小数，而是指：

在 数值靠近某个数值（如 1.0）时的最小可分辨间隔

这个间隔是由 尾数位的长度和指数位的大小共同决定的，所以不是简单地说“小数点后能表示几位”。

举个例子：

FP16 的尾数只有 10 位，它表示 1.000 和 1.001 是区分得了的，但 1.0005 就分不清了。

---

❌ INT8 是整数类型

INT8 不是浮点数，所以它没有尾数位，也就不能表示小数。

数据类型	是否有小数？	小数精度？
FP32	有	高精度（7~8位十进制）
FP16	有	低精度（~3位十进制）
BF16	有	很低（12位十进制）
INT8	❌ 无	精度=1，不能表示小数

---

✅ 最后总结一句话

表格里的“精度举例”并不是描述能表示多少位小数，而是描述：在接近某个数值时，两个可表示数之间的最小差距（Δ）是多少。

这个是由尾数位和指数范围共同决定的数值分辨率，不是简单的小数位数概念。

---

如果你需要，我可以提供一个 Python 脚本，对比 FP32/FP16/BF16 在不同数值下的实际精度差值（ULP），比如：

import numpy as np
np.nextafter(1.0, 2.0, dtype=np.float32) - 1.0  # 输出 FP32 的最小精度