2015 HNU Warm Up 04

这一套题是13年长沙现场赛。

A - Alice's Print Service
从后往前推，如果后面的最低标准线比前面低，继承后者。

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
using namespace std;
#define MAXN 100100
#define LL __int64
#define INF 12345678987654321LL

template <class T>
inline int RD(T &x)
{
        x = 0;
        char ch = getchar();
        while(!isdigit(ch)) { if(ch == '-') exit(0); ch = getchar(); if(ch == EOF) return 0; }
        while(isdigit(ch)) { x *= 10; x += ch - '0'; ch = getchar(); }
        return 1;
}
template <class T0, class T1>
inline int RD(T0 &x0, T1 &x1) { return RD(x0) + RD(x1); }

inline LL min(LL a, LL b)
{
    return a > b ? b : a;
}

LL s[MAXN], p[MAXN], f[MAXN];

int main()
{
//    freopen("A.in", "r", stdin);

    int T; RD(T);
    while(T--)
    {
        int n, m, q; RD(n, m);
        for(int i = 0; i < n; i++) RD(s[i], p[i]);
        s[n] = f[n] = INF;
        for(int i = n - 1; i; i--) f[i] = min(f[i + 1], s[i] * p[i]);
        n++;

        while(m--)
        {
            RD(q);
            int pos = upper_bound(s, s + n, q) - s - 1;
            LL ans = min(q * p[pos], f[pos + 1]);
            printf("%I64d\n", ans);
        }
    }
    return 0;
}

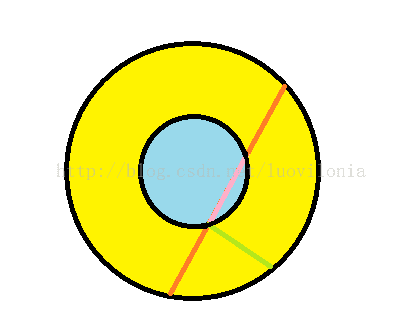
C - Collision

解一元二次方程，分无解（不会进入），有解但是不会经过解所在区域（远离圆心），有解（会进入）。

有解又分碰撞和不碰撞，同样的处理方法：解方程。

此时要求一根橙线和一个绿线的时间，其中绿线和橙线等长。于是转化为两个方程的两个解的相差长度相减。

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <math.h>
using namespace std;
#define LL long long
#define MAXN 510
#define eps 1e-8


double Rm, R, r, x, y, vx, vy;
double work()
{
    double a, b, c, tc;
    //(x + vx * t) ^ 2 + (y + vy * t) ^ 2 - (R + r) ^ 2 >= 0
    a = vx * vx + vy * vy;
    b = 2 * (x * vx + y * vy);
    c = x * x + y * y;

    //不会进入
    if((4*a*c - b*b) >= 4*a*(R + r)*(R + r) || b >= 0) return 0.0;
    //不会撞
    if((4*a*c - b*b) >= 4*a*(Rm + r)*(Rm + r))
    {
        tc = c - (R + r) * (R + r);
        return sqrt(b*b - 4*a*tc) / a;
    }

    tc = c - (R + r) * (R + r);
    double t1 = sqrt(b*b - 4*a*tc) / a;
    tc = c - (Rm + r) * (Rm + r);
    double t2 = sqrt(b*b - 4*a*tc) / a;
    return t1 - t2;
}

int main()
{
//    freopen("C.in", "r", stdin);

    while(~scanf("%lf%lf%lf%lf%lf%lf%lf", &Rm, &R, &r, &x, &y, &vx, &vy))
    {
        printf("%.10f\n", work() + eps);
    }
    return 0;
}

D - Arnold

题目大意：有一种图像变化，可以把一张N x N的图片中的所有点(x, y)，变化为((x+y)%N, (x+2y)%N)，问这样变几次又可以得到原来的图片。
观察后能得出其实这是一个广义fib数列：f1 和 f2 先给出初值x，y，然后f3 = f1 + f2 = x + y，f4 = f3 + f2 = x + y + y = x + 2y。
然后转化为求广义fib数列的循环节，ACdreamer的文章讲的很好。

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <math.h>
using namespace std;
#define N 2
#define OT printf
#define MAXN 10100
#define LL unsigned long long
#define INF 0x7f7f7f7f
#define RUN(x) freopen(#x, "r", stdin);
#define REP(i, n) for(i = 0; i < n; i++)
#define FOR(i, s, e) for(i = s; i <= e; i++)
#define DWN(i, s, e) for(i = e; i >= s; i--)

LL gcd(LL a, LL b) { return a % b ? gcd(b, a % b) : b; }
LL lcm(LL a, LL b) { return a / gcd(a, b) * b; }
//(a * b) % n
LL Multi_mod(LL a, LL b, LL n) { LL s = 0; while(b) { if(b & 1) s = (s + a) % n; a = (a + a) % n; b >>= 1; } return s; }
//(a ^ b) % n
LL Pow_mod(LL a, LL b, LL n) { LL s = 1; while(b) { if(b & 1) s = Multi_mod(s, a, n); a = Multi_mod(a, a, n); b >>= 1; } return s; }

struct Matrix
{
    LL mat[N][N];
    Matrix() {}
    void clr() { memset(mat, 0, sizeof(mat)); }
    Matrix E()
    {
        Matrix e; e.clr();
        int i; REP(i, N) e.mat[i][i] = 1;
        return e;
    }
    Matrix Multi_mod(const Matrix &argu, LL mod)
    {
        int i, j, k;
        Matrix ret; ret.clr();
        REP(i, N) REP(j, N) REP(k, N)
        {
            ret.mat[i][j] += mat[i][k] * argu.mat[k][j];
            ret.mat[i][j] %= mod;
        }
        return ret;
    }
    Matrix Pow_mod(LL n, LL mod)
    {
        Matrix p = (*this), res = E();
        while(n) { if(n & 1) res = res.Multi_mod(p, mod); p = p.Multi_mod(p, mod); n >>= 1; }
        return res;
    }
    void out() { int i, j; REP(i, N) { REP(j, N) OT("%d ", mat[i][j]); puts(""); } }
};

LL f0 = 0, f1 = 1;
LL fn, fn_1;
void getFib(LL n, LL mod)
{
    Matrix A;
    A.mat[0][0] = A.mat[1][0] = A.mat[0][1] = 1;
    A.mat[1][1] = 0;
    Matrix B = A.Pow_mod(n, mod);
    fn_1 = (f1 * B.mat[1][0] + f0 * B.mat[1][1]) % mod;
    fn = (f1 * B.mat[0][0] + f0 * B.mat[0][1]) % mod;
}

//勒让德符号
//x^2 mod p = a 方程有解，那么a是模p的平方剩余, 返回1；
//如果方程无解，那么a是模p的平方非剩余， 返回-1。
//欧拉判别法 (a|p) = a^((p-1)/2) % p
int legendre(LL a, LL p)
{
    if(Pow_mod(a, ((p - 1) >> 1), p) == 1) return 1;
    return -1;
}

LL fac[MAXN];
LL get_len(LL m)
{
    if(m == 2) return 3;
    if(m == 3) return 8;
    if(m == 5) return 20;

    LL p;
    if(legendre(5, m) == 1) p = m - 1;
    else p = 2 * (m + 1);

    int cnt = 0;
    for(LL i = 1; i * i <= p; i++) if(p % i == 0)
    {
        LL x = i, y = p / i;
        getFib(x, m);
        if(fn_1 == f0 && fn == f1) return x;
        if(y != x) fac[cnt++] = y;
    }
    while(cnt--)
    {
        getFib(fac[cnt], m);
        if(fn_1 == f0 && fn == f1) return fac[cnt];
    }
    return -1;
}

LL find_loop(LL n)
{
    LL ans = 1, x = n, len, s;
    for(LL i = 2; i * i <= x; i++) if(x % i == 0)
    {
        len = get_len(i);
        x /= i;
        while(x % i == 0) x /= i, len *= i;
        ans = lcm(ans, len);
    }
    if(x > 1)
    {
        len = get_len(x);
        ans = lcm(ans, len);
    }
    return ans / 2;
}

int main()
{
//    freopen("D.in", "r", stdin);

    LL n;
    while(~scanf("%I64u", &n)) printf("%I64u\n", find_loop(n));
    return 0;
}