在模式识别领域谈随机变量

概率论之所以难，是因为它抽象，没有落点，模式识别正好是它的一个落点。

从随机现象到样本空间到随机变量的取值。然后就可以谈分布了。有了分布谈采样，就有了样本。

• 随机现象
  

• 样本空间
  
  

• 随机变量
  为了进行定量的数学处理，必须把随机现象的结果数量化，这就是引入随机变量的原因。
  随机变量既是变量也是函数。
  从变量的角度来看，随机变量是指在随机试验或者随机过程中可能取不同数值的一种变量，它的数值受随机因素影响，无法事先确切预知。
  
  
  从函数的角度来看，随机变量是定义在样本空间（随机试验所有可能结果组成的集合）上的一个实值函数。它将随机试验的所有可能结果（样本点）映射到实数集合上，每一个样本点对应一个实数值。随机变量的本质是对不确定事件结果的一种量化表示，使得原本非数值化的随机现象可以用数学语言来描述。
  
  随机变量结合了变量的不确定性属性与函数的映射特性，它通过函数的方式将随机事件的结果量化，并通过概率论的语言来描述这些结果出现的可能性分布。

• 取值空间
  随机变量的取值空间，也称为随机变量的定义域或者值域，是随机变量所有可能取值的集合。

用Fisher鸢尾属植物数据集（Iris dataset）（1936）举例。
随机现象是不同的鸢尾花有不同的长势。
样本点是一个个鸢尾花。
样本空间是样本点的集合。

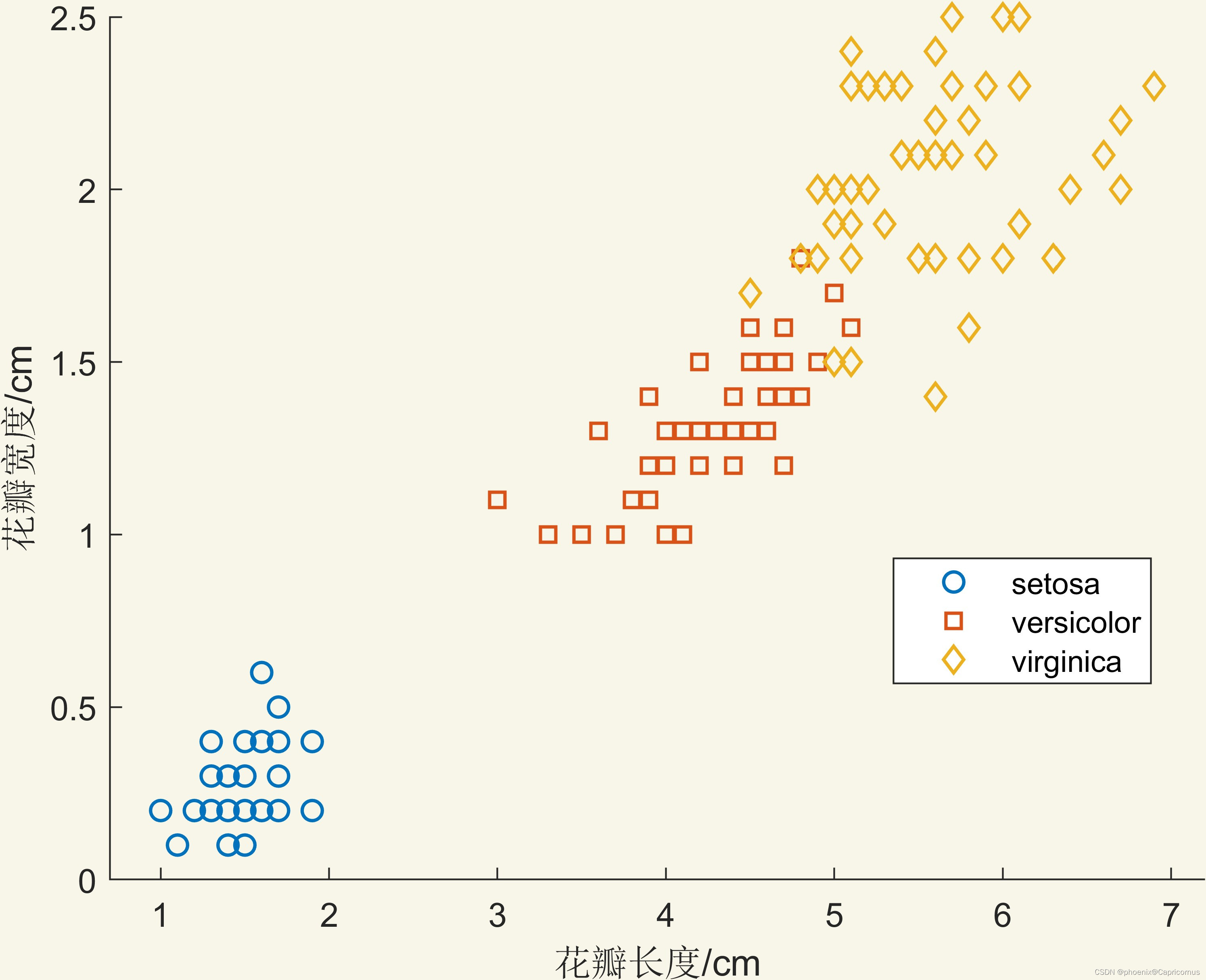
随机变量是测量鸢尾花的花瓣长度（petal length）和花瓣宽度（petal width），取值是某个区间的实数，单位是cm。
随机变量是样本空间到取值空间的映射。在模式识别中，取值空间就是特征空间。
特征本身就是实数，如花瓣长度和花瓣宽度本身就是实数，所以在模式识别中，样本空间和特征空间的概念相同。
所以，样本空间就是取值空间，取值空间就是特征空间，样本空间就是特征空间。
该图是二维随机变量的样本空间，也是特征空间。

终于知道Duda模式分类中类别为什么用$\omega$了，原来出处在统计学中的样本空间。