DDPM学习笔记

对了，我开通了微信公众号，计划是两边会同步更新，并逐步的会将博客上的文章同步至公众号中。感兴趣的朋友可以搜索“里先森sements”来关注，欢迎来玩~！

---

参考：

1. 扩散模型之DDPM - 知乎: https://zhuanlan.zhihu.com/p/563661713
2. 【生成式AI】淺談圖像生成模型 Diffusion Model 原理 - YouTube: https://www.youtube.com/watch?v=azBugJzmz-o&ab_channel=Hung-yiLee
3. 【生成式AI】Diffusion Model 原理剖析 (1/4) (optional) - YouTube: https://www.youtube.com/watch?v=ifCDXFdeaaM
4. 【生成式AI】Diffusion Model 原理剖析 (2/4) (optional) - YouTube: https://www.youtube.com/watch?v=73qwu77ZsTM&ab_channel=Hung-yiLee
5. 【生成式AI】Diffusion Model 原理剖析 (3/4) (optional) - YouTube: https://www.youtube.com/watch?v=m6QchXTx6wA&t=602s&ab_channel=Hung-yiLee
6. 【生成式AI】Diffusion Model 原理剖析 (4/4) (optional) - YouTube: https://www.youtube.com/watch?v=67_M2qP5ssY&ab_channel=Hung-yiLee
7. [2006.11239] Denoising Diffusion Probabilistic Models: https://arxiv.org/abs/2006.11239
8. [2208.09392] Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise: https://arxiv.org/abs/2208.09392
9. [2304.08577] Avatars Grow Legs: Generating Smooth Human Motion from Sparse Tracking Inputs with Diffusion Model: https://arxiv.org/abs/2304.08577
10. Maximum Likelihood and Entropy — thirdorderscientist: https://thirdorderscientist.org/homoclinic-orbit/2013/4/1/maximum-likelihood-and-entropy
11. 大数定律 - 维基百科，自由的百科全书: https://zh.wikipedia.org/wiki/%E5%A4%A7%E6%95%B8%E6%B3%95%E5%89%87
12. 由浅入深了解Diffusion Model - 知乎: https://zhuanlan.zhihu.com/p/525106459
13. [2208.11970] Understanding Diffusion Models: A Unified Perspective: https://arxiv.org/abs/2208.11970

现如今绝大多数的扩散模型（Diffusion Model）追本溯源都离不开《Denoising Diffusion Probabilistic Models》（DDPM）^[7]这篇论文。了解 DDPM 背后的机理可以帮助我们快速上手类似结构的扩散模型。本文实质上是在学习李宏毅老师的Diffusion Model课程^[2-6]与小小将的文章^[1]后，结合部分个人理解整理的学习笔记。文中大部分图片都是出自李宏毅老师课程视频的PPT截图。

1 - Diffusion Model概览

DDPM所做的工作，是从一个随机噪声中采样出一张含有特定语义的图像。如果将DDPM比作一个雕塑家，而随机噪声是一块原石，DDPM所作的工作实质上和米开朗琪罗的名言所述一致。

The sculpture is already complete within the marble block, before I start my work. It is already there, I just have to chisel away the superfluous material. - Michelangelo

在我开始工作之前，雕塑已经在大理石块内完成了。它已经在那里了，我只需要把多余的材料凿掉。——米开朗基罗

概括的来看，我们可以从DDPM的网络结构、数据集以及优化目标这三个方面来着手，对DDPM形成一个大致上的了解，而DDPM中的数学理论将在第二部分中进行讨论。

1.1 - DDPM运作机理

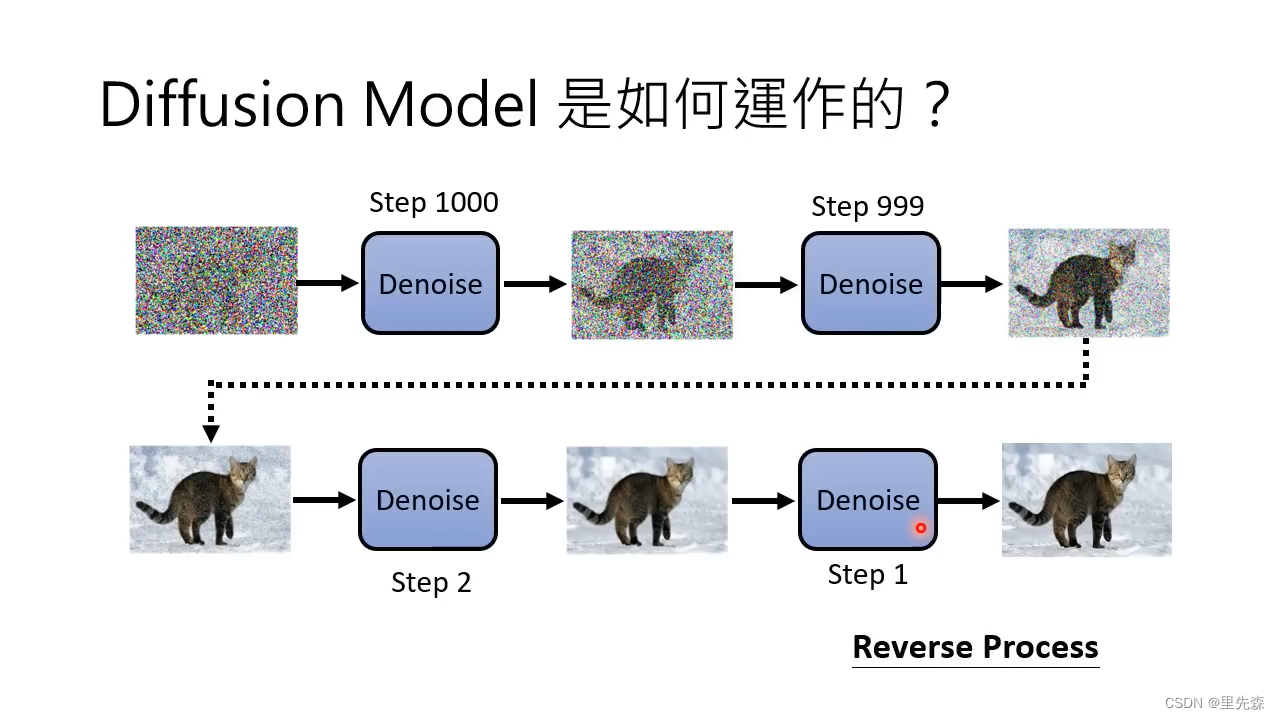
上图直观的展示了DDPM（或者说这类Diffusion Model）从随机噪音生成有语义的图片的过程。这个过程也被称为反向过程Reverse Process，其与生成训练数据的扩散过程Diffusion process（Forward prcess）相对。图中的Denoise模组是预先训练好的，从最开始的全随机噪声开始，按照预先设计好的处理步长，Denoise模组一步一步削减其中不需要的噪声数据，将埋没在其中的图像数据剥离出来。

这也是为什么说Diffusion Model与雕塑家类似，只不过在这里带有噪声的图像数据是原石，Diffusion Model对其进行雕琢，将埋没在其中的图像解放了出来。当然，也并非一定要从随机噪声这块“原石”开始雕琢，诸如Cold Diffusion^[8]之类的研究表明，扩散模型的前向阶段并不依赖与高斯噪音。对图像进行模糊、遮蔽等退化行为，模型在生成时仍然有好的结果。

由于整个过程中所使用的Denoise模组都是同一个，但每一步中输入的图片差异很大（例如在Step 1000到Step 999，要削减的噪声较多，而Step 2到Step 1要削减掉的噪声数据只需要一捏捏），单纯让网络自己去判断要削减的噪声量可能较难达到理想效果。因此我们还需要给Denoise模组输入一个标识，告诉它当前运行到了哪个步骤，让它根据这个步骤去斟酌要削减掉的噪声量。

在Denoise模组内部，实际上并非是搭建了一个端到端的网络。让网络吃一个带噪声的图，吐出一个削减掉部分噪声图是一个理所当然的想法。但是这样的网络必须复杂到一定地步，它能够察觉到输入的噪声图像中所蕴涵的语义信息，然后再根据这个语义信息，去对输入图像进行去噪处理。这样复杂的网络往往很难被训练出来，或者较难达到理想的训练的效果。因此我们可以退而求其次，构建一个Noise Predicter网络，让网络做噪声预测工作。相比于直接构建一个端到端的网络，单纯预测噪声的Noise Predicter网络要更好训练。这个网络接收图像与当前步骤数，预测要删减掉的噪声。在Denoise模组的输出端，将Noise Predicter网络预测的噪声图与输入图相减，从而得到去噪后的图像。

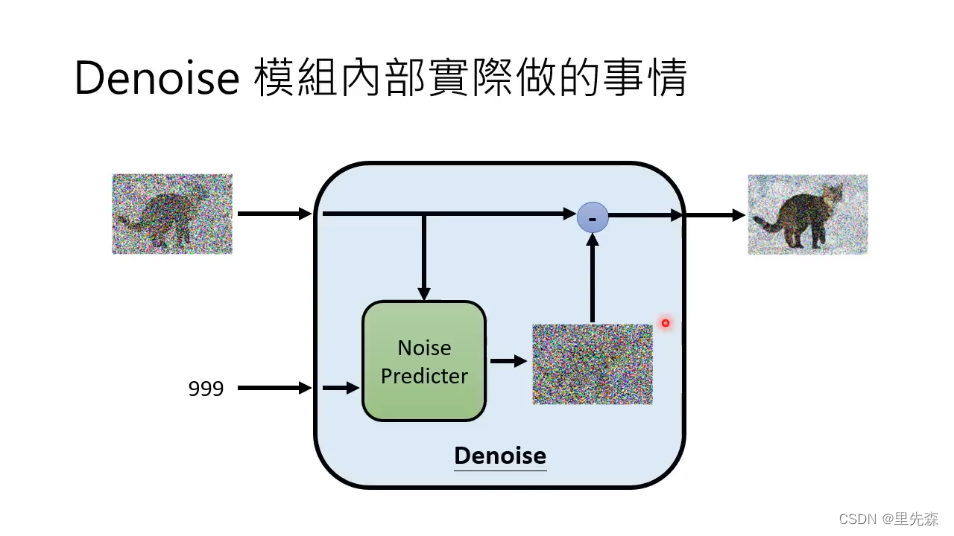
1.2 - 网络结构

在DDPM论文中，作者使用PixelCNN++作为backbone并在上面进行了一些微调。事实上也可以对任务需求尝试使用其他的网络架构，例如在Meta AI的一项工作^[9]中，就使用了简单的全连接架构来接收序列数据。

1.3 - 优化目标与数据集

大致了解DDPM的运作机理之后，便可以开始考虑如何训练Denoise模块，或者说其中的Noise Predicter网络了。由于训练的Noise Predicter是预测噪声的网络，那么需要准备的数据自然就是成对的带有噪声与不带噪声的数据。这个问题可以通过简单的构建步骤来解决：从现有的图像数据集中取一张图片，逐步的对其添加噪声。这样操作既可以得到噪声不断增多直至完全是随机噪声的数据，还可以得到每次添加噪声时的步骤号。这个过程也被称为Forward Process（Diffusion Process）。

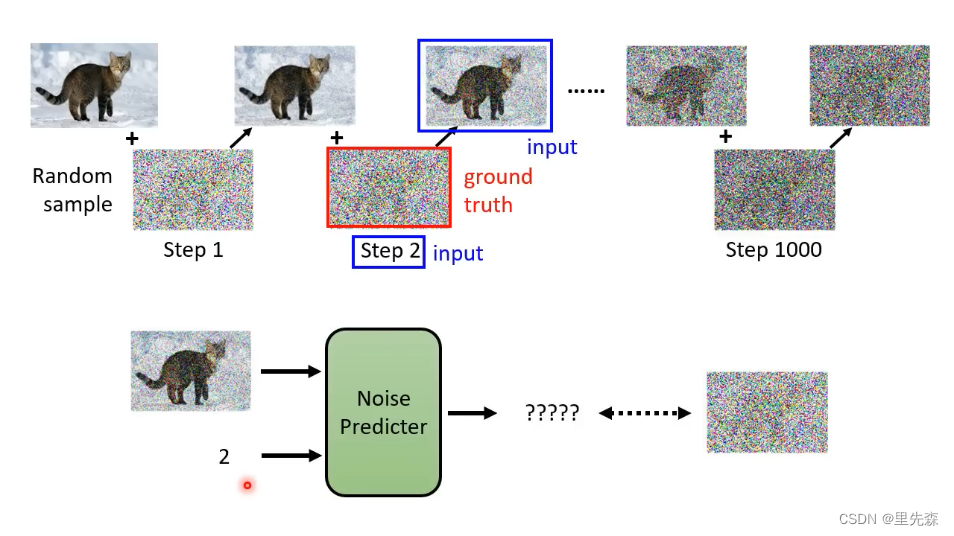
如此一来我们便可以得到Noise Predicter网络所需的训练资料了，还记得Noise Predicter网络需要的输入输出嘛？它需要带有噪声的图片以及步骤号作为输入，输出则是它预测的为了到达上一Step所要减去的噪声。由于整个前向过程都是有迹可循的，因此噪声的ground truth是已知的。将添加的真实噪声与Noise Predicter网络预测的噪声作比较，便可以知道Noise Predicter网络当下的训练效果，从而得到优化方向。

上图便是DDPM方法中所使用的训练以及推理流程。你会发现似乎实际的代码实现与先前的机理介绍有些许出入，这也使得训练与推理看上去似乎很简单，但实际上其中暗藏玄机。DDPM在实际实现中所做的调整优化以及其中的数学理论将在下一节中进行阐述。

2 - 从数学角度理解Diffusion Model

对图像生成模型，我们需要考虑某个图像$x$在真实世界（或者说我们的数据集）中出现的机率$P_{data}(x)$，以及在神经网络$\theta$的推理结果中出现的机率$P_{\theta }(x)$。为了便于理解，我们以猫咪照片数据集为例。在这个数据集中，出现狸花猫的照片的机率$P_{data}(狸花猫)$会很大，但是出现一只贵宾犬照片的机率$P_{data}(贵宾犬)$将非常小。

$P_{data}(x)$与$P_{\theta }(x)$越接近，说明这张图片在真实世界与神经网络推理中出现的机率越近似，也就意味着神经网络$\theta$输出的图片越真实，或者说越接近我们数据集中的图像。例如我们有一个十分优秀的图像生成模型，它的$P_{data}(x)$与$P_{\theta }(x)$十分接近，那么让其进行猫咪图像的生成任务时，它生成的猫咪图像将真假难辨。同时，它也不大可能生成看上去不太像真实世界中的猫咪或者一只狗狗的图像。

在训练神经网络时，我们可以从数据集中提取数据 { x 1 , x 2 , . . . , x m } \{x^1,x^2,...,x^m\} {x1,x2,...,xm}，期望的目标是神经网络能够模仿生成与数据集真假难辨的图像。对于每一个数据$x^i$，我们希望$P_{\theta }(x^i)$的值越大越好。为此，我们可以构建最大似然估计函数
$${\theta }^{\ast }=\arg \underset{\theta }{\max }\prod _{i=1}^m{P}_{\theta }(x^i)\text{\hspace{1em}(1)}$$
其中，${\theta }^{\ast }$指能最大概率生成类似数据集中图像的神经网络参数。

2.1 *最大似然与最小KL散度（Maximum likelihood and Minimize KL-Divergence）

你可能会有疑问：“为什么求取符合上式的神经网络参数${\theta }^{\ast }$就能使得$P_{data}(x)$与$P_{\theta }(x)$越接近？”。事实上，最大似然估计实质上与我们常用的度量两个概率分布相似度的指标——KL散度（Kullback-Leibler Divergence）是等价的，求取最大似然估计实质上就是在最小化$P_{data}(x)$与$P_{\theta }(x)$之间的KL散度。可以通过公式推导来证明这一点，对上式右侧的$\prod _{i=1}^m{P}_{\theta }(x^i)$取对数，不影响等式，可得

$${\theta }^{\ast }=\arg \underset{\theta }{\max }\log \prod _{i=1}^m{P}_{\theta }(x^i)\text{\hspace{1em}(2)}$$
根据对数的性质，上式的连乘可以写为
$${\theta }^{\ast }=\arg \underset{\theta }{\max }\sum _{i=1}^m\log P_{\theta }(x^i)\text{\hspace{1em}(3)}$$
根据大数定律，当我们的样本数量足够多时，$\sum _{i=1}^m\log P_{\theta }(x^i)$的算数平均值应当收敛到其期望值^[10,11]。那么我们又可将上式近似为
$${\theta }^{\ast }\approx \arg \underset{\theta }{\max }{E}_{x\sim P_{data}}[\log P_{\theta }(x)]\text{\hspace{1em}(4)}$$
其中，$E_{x\sim P_{data}}[\log P_{\theta }(x)]$表示从$P_{data}$中取出的样本$x$，计算$\log P_{\theta }(x)$的期望。注意，此处我们仅做定性分析，并未计算等式右侧的算数平均值。根据期望值的定义，我们可得
$${\theta }^{\ast }=\arg \underset{\theta }{\max }\int P_{data}(x)\log P_{\theta }(x)\mathrm{d}x\text{\hspace{1em}(5)}$$
在等式右侧添加与$\theta$无关的$P_{data}$项，不影响等式，可得
$${\theta }^{\ast }=\arg \underset{\theta }{\max }\int P_{data}(x)\log P_{\theta }(x)\mathrm{d}x-\int P_{data}(x)\log P_{data}(x)\mathrm{d}x\text{\hspace{1em}(6)}$$
整理上式
$${\theta }^{\ast }=\arg \underset{\theta }{\max }\int P_{data}(x)\log \frac{P_{\theta }(x)}{P_{data}(x)}\mathrm{d}x\text{\hspace{1em}(7)}$$
可以将上式从$\arg \underset{\theta }{\max }$改写为$\arg \underset{\theta }{\min }$
$${\theta }^{\ast }=\arg \underset{\theta }{\min }\int P_{data}(x)\log \frac{P_{data}(x)}{P_{\theta }(x)}\mathrm{d}x\text{\hspace{1em}(8)}$$
等式右侧项即KL散度
$${\theta }^{\ast }=\arg \underset{\theta }{\min }KL(P_{data}\parallel P_{\theta })\text{\hspace{1em}(9)}$$
综上所述，我们证明了最大似然即是等于最小KL散度。因此在进行模型优化时，求取最大似然估计实质上就是在最小化$P_{data}(x)$与$P_{\theta }(x)$之间的KL散度。

2.2 扩散过程（前向过程）

所谓扩散过程（前向过程），即往图片上加噪声的过程。虽然这个步骤无法做到图片生成，但是这是理解diffusion model以及构建训练样本至关重要的一步。在扩散过程中，$x_0$是理想的清晰图像，随着下标逐渐增大，图像中的噪声逐渐增多，直至$x_T$成为全噪声图像。由图像$x_0$扩散到全噪声图像$x_T$的过程$q(x_T\mid x_0)$可以写成如下形式
$$q(x_T\mid x_0)=\prod _{t=1}^{T}q(x_t\mid x_{t-1})=q(x_1\mid x_0)q(x_2\mid x_1)\cdots q(x_T\mid x_{T-1})\text{\hspace{1em}(10)}$$
根据论文中的定义，从$x_{t-1}$到$x_t$的扩散过程$q(x_t\mid x_{t-1})$定义如下
$$x_t=\sqrt{1-{\beta }_t}\cdot x_{t-1}+\sqrt{{\beta }_t}\cdot {ϵ}_{t-1}\text{\hspace{1em}(11)}$$
其中，$ϵ\sim \mathcal{N}(0,I)$。 { β t ∈ ( 0 , 1 ) } t = 1 T \left\{ \beta_t \in (0,1) \right\}^{T}_{t=1} {βt​∈(0,1)}t=1T​是预先定义好的一组高斯分布方差的超参数。在DDPM中，作者定义${\beta }_t$的值随着下标$t$的增大而递增，即${\beta }_1<{\beta }_2<\dots {\beta }_T$。

关于为何DDPM中如此定义前向过程，知乎上的作者ewrfcas给出了他的分析^[12]：

…一开始笔者一直不清楚为什么diffusion的均值每次要乘上 $\sqrt{1-{\beta }_t}$ 。明明${\beta }_t$只是方差系数，怎么会影响均值呢？替换为任何一个新的超参数，保证它<1，也能够保证值域并且使得最后均值收敛到0（但是方差并不为1）。…可以发现当 $T\to \infty$ ，$x_T\sim \mathcal{N}(0,I)$ 。所以$\sqrt{1-{\beta }_t}$的均值系数能够稳定保证 $x_T$最后收敛到方差为1的标准高斯分布，且在推导中也更为简洁优雅。

按照公式(11)，我们的确可以一张一张的生成供模型训练的数据，但是这未免太过繁琐。寻求一种通过$x_0$以及$\beta$来快速直接得到所需的$x_t$图像有助于加速训练时的数据集准备过程，并且节约空间占用。根据定义，我们试写由$x_0$扩散到$x_1$，以及由$x_1$扩散到$x_2$的过程
$$\{\begin{array}{c}{x}_1=\sqrt{1-{\beta }_1}\cdot x_0+\sqrt{{\beta }_1}\cdot {ϵ}_0\\ x_2=\sqrt{1-{\beta }_2}\cdot x_1+\sqrt{{\beta }_2}\cdot {ϵ}_1\end{array}\text{\hspace{1em}(12)}$$
合并上式，我们有
$$x_2=\sqrt{1-{\beta }_2}\cdot \left[\sqrt{1-{\beta }_1}\cdot x_0+\sqrt{{\beta }_1}\cdot {ϵ}_0\right]+\sqrt{{\beta }_2}\cdot {ϵ}_1\text{\hspace{1em}(13)}$$
设${\alpha }_t=1-{\beta }_t$，$\overline{{\alpha }_t}={\prod }_{i=1}^T{\alpha }_i$，整理上式，我们有
$$x_2=\sqrt{{\alpha }_2{\alpha }_1}\cdot x_0+\left(\sqrt{{\alpha }_2(1-{\alpha }_1)}\cdot {ϵ}_0+\sqrt{1-{\alpha }_2}\cdot {ϵ}_1\right)\text{\hspace{1em}(14)}$$
由于独立高斯分布的可加性，即$\mathcal{N}(0,{\sigma }_1^{2}I)+\mathcal{N}(0,{\sigma }_2^{2}I)\sim \mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)I)$，我们有
$$\{\begin{array}{c}\sqrt{{\alpha }_2\left(1-{\alpha }_1\right)}\cdot {ϵ}_0\sim N\left(0,{\alpha }_2\left(1-{\alpha }_1\right)I\right)\\ \sqrt{1-{\alpha }_2}\cdot {ϵ}_1\sim N\left(0,\left(1-{\alpha }_2\right)I\right)\end{array}\text{\hspace{1em}(15)}$$
则
$$\begin{array}{rl}\sqrt{{\alpha }_2(1-{\alpha }_1)}\cdot {ϵ}_0+\sqrt{1-{\alpha }_2}\cdot {ϵ}_1& \sim N\left(0,\left[{\alpha }_2\left(1-{\alpha }_1\right)+(1-{\alpha }_2)\right]I\right)\\ & =N\left(0,\left(1-{\alpha }_2{\alpha }_1\right)I\right)\end{array}\text{\hspace{1em}(16)}$$
因此可以混合式(14)中两个高斯分布得到标准差为$\sqrt{1-{\alpha }_2{\alpha }_1}$的新的正态分布$\overline{{ϵ}_2}$，将其改写为
$$x_2=\sqrt{{\alpha }_2{\alpha }_1}\cdot x_0+\sqrt{1-{\alpha }_2{\alpha }_1}\cdot \overline{{ϵ}_2}\text{\hspace{1em}(17)}$$
同理，可以类比得到直接由$x_0$扩散到$x_t$的过程$q(x_t|x_0)$
$$x_t=\sqrt{\overline{{\alpha }_t}}\cdot x_0+\sqrt{1-\overline{{\alpha }_t}}\cdot \overline{{ϵ}_t}\text{\hspace{1em}(18)}$$

2.3推理过程（去噪过程）

根据前文定义的最大似然函数可知，我们的优化目标是寻求一个最佳的网络参数${\theta }^{\ast }$，可使得模型生成每个数据集中的图像$x$的概率$P_{\theta }(x)$最大。但是直接寻求它的最大值是一个相当复杂的问题，因此我们的优化目标可以转变为尽可能提升$P_{\theta }(x)$的下界（lower bound）。这引出了两个问题：如何求解$P_{\theta }(x)$，以及如何寻找其下界。

2.3.1求解$P_{\theta }(x)$

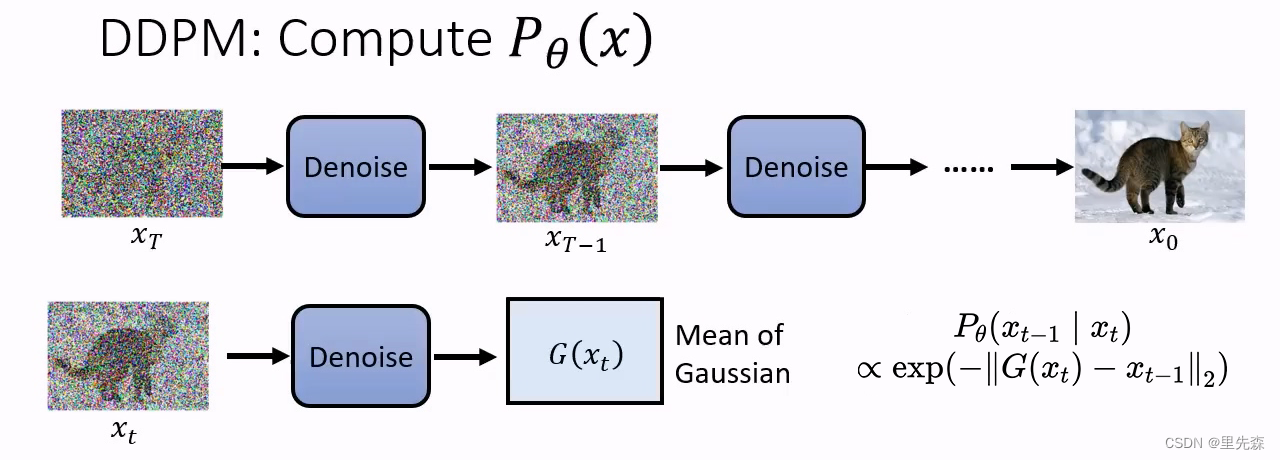
DDPM生成图片的过程是从完全随机的噪声图像$x_T$开始，逐步使用噪声预测模型预测并去除噪声，最终得到干净的图像$x_0$。为了知道我们的模型$\theta$生成理想图像$x_0$的概率$P_{\theta }(x_0)$，我们可以从DDPM每一个步骤的生成概率逐步后推。假设我们现处于步骤$t$，我们想知道当前的模型$\theta$在给定图像$x_t$的情况下，生成理想中的下一步骤$t-1$的图像$x_{t-1}$的概率$P_{\theta }(x_{t-1}\mid x_t)$有多少。设模型根据图像$x_t$生成的去噪声图像为$G(x_t)$，最简单的衡量方式便是当$G(x_t)$与$x_{t-1}$完全相同时，$P_{\theta }(x_{t-1}\mid x_t)$为1，反之则为零
$$P_{\theta }(x_{t-1}\mid x_t)=\{\begin{array}{llc}& 1,& G(x_t)=x_{t-1}\\ & 0,& G(x_t)\ne x_{t-1}\end{array}\text{\hspace{1em}(19)}$$
然而，正如古话所说，天下没有两片完全相同的树叶。模型生成的图像与理想图像完全相同这件事发生的概率实在太低了，这将导致我们计算出来的$P_{\theta }(x_{t-1}\mid x_t)$几乎全都是0。为了解决这个问题，我们不妨设模型生成的$G(x_t)$代表一个高斯分布，其值与该高斯分布的平均值相同，而$P_{\theta }(x_{t-1}\mid x_t)$可以看作$G(x_t)$与$x_{t-1}$之间的距离
$$P_{\theta }(x_{t-1}\mid x_t)\propto \exp (-{\Vert G(x_t)-x_{t-1}\Vert }_2)\text{\hspace{1em}(20)}$$
在这里，我们对$G(x_t)$与$x_{t-1}$之差的二范数取指数，这个值将与$P_{\theta }(x_{t-1}\mid x_t)$呈正比关系。与前面的衡量方式相同，当$G(x_t)$与$x_{t-1}$完全相同时，$P_{\theta }(x_{t-1}\mid x_t)$为1。而当$G(x_t)$与$x_{t-1}$存在差异时，差异越小值越接近于1，差异越大值将无限靠近0。根据DDPM的推理流程，计算模型最终生成理想图像$x_0$的概率$P_{\theta }(x_0)$可以写为

$$P_{\theta }(x_0)=\underset{x_1:x_t}{\int }P(x_T)P_{\theta }(x_{T-1}\mid x_T)\dots P_{\theta }(x_{t-1}\mid x_t)\dots P_{\theta }(x_0\mid x_1)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(21)}$$
其中，$x_1:x_T$指从$x_T$到$x_1$，$P(x_T)$则是从随机噪声中采样出图像$x_T$的机率。

2.3.2 求解$P_{\theta }(x_0)$下界

为便于求解，寻求$P_{\theta }(x_0)$的下界可以转换为寻求$\log P_{\theta }(x_0)$的下界。而对于$\log P_{\theta }(x_0)$，有以下等式成立
$$\log P_{\theta }(x_0)=\underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log P_{\theta }(x_0)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(22)}$$
其中，$q(x_1:x_T\mid x_0)$可以是任意形式的概率分布，并不影响上式的成立。根据贝叶斯定律，上式可写为
$$\log P_{\theta }(x_0)=\underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{P_{\theta }(x_0:x_T)}{P_{\theta }(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(23)}$$
对括号内的式子进行拆分，可得
$$\log P_{\theta }(x_0)=\underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\cdot \frac{q(x_1:x_T\mid x_0)}{P_{\theta }(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(24)}$$
利用对数函数的性质，可将上式整理如下
$$\begin{gathered} \log P_{\theta }(x_0)=\underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T \\ +\underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{q(x_1:x_T\mid x_0)}{P_{\theta }(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(25)} \end{gathered}$$
根据KL散度定义，有
$$\begin{gathered} \underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{q(x_1:x_T\mid x_0)}{P_{\theta }(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T \\ =KL\left[q(x_1:x_T\mid x_0)\Vert P_{\theta }(x_1:x_T\mid x_0)\right]\text{\hspace{1em}(26)} \end{gathered}$$
而KL散度始终大于等于0，也就是说在考虑$\log P_{\theta }(x_0)$的下界时，KL散度部分的公式可以省去，可得
$$\log P_{\theta }(x_0)\ge \underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T\text{\hspace{1em}(27)}$$
根据期望的定义，我们有
$$\begin{gathered} \underset{x_1:x_T}{\int }q(x_1:x_T\mid x_0)\cdot \log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\right)\mathrm{d}{x}_1:x_T \\ =E_{q(x_1:x_T\mid x_0)}\left[\log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\right)\right]\text{\hspace{1em}(28)} \end{gathered}$$
将其带入前式，可得
$$\log P_{\theta }(x_0)\ge E_{q(x_1:x_T\mid x_0)}\left[\log \left(\frac{P_{\theta }(x_0:x_T)}{q(x_1:x_T\mid x_0)}\right)\right]\text{\hspace{1em}(29)}$$
综上我们可以知道$\log P_{\theta }(x_0)$的下界，如何尽可能的提升该下界便是我们神经网络的优化目标。事实上，$q(x_1:x_T\mid x_0)$就是Diffusion模型前向的扩散过程。然而，公式(29)并不便于直接计算，需要对其进行化简。化简的过程过于繁琐，在此我们只取用结果，感兴趣的各位可参考论文^[13]进行了解。

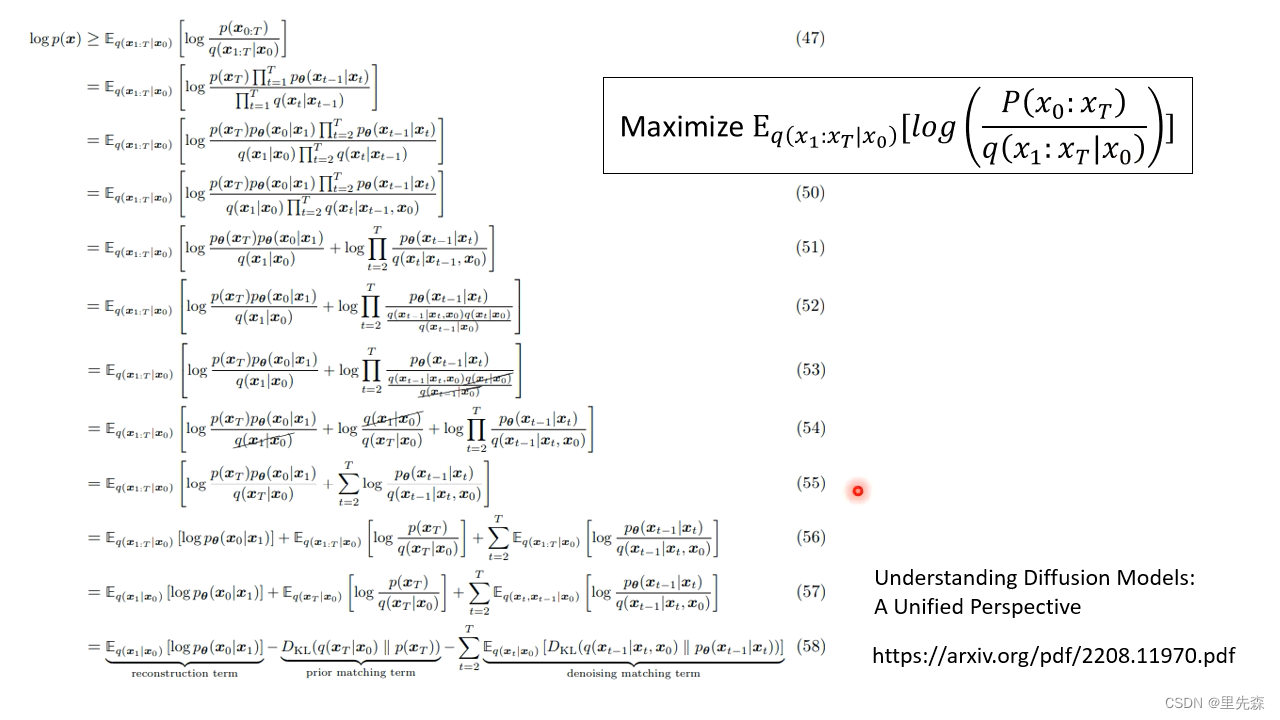
总而言之，最终我们的优化目标变为如何提升下式的值
$$\begin{array}{rl}{\mathrm{E}}_{q\left(x_1\mid x_0\right)}\left[\log P_{\theta }\left(x_0\mid x_1\right)\right]& -KL\left(q\left(x_T\mid x_0\right)\Vert P\left(x_T\right)\right)\\ & -\sum _{t=2}^T{\mathrm{E}}_{q\left(x_t\mid x_0\right)}\left[KL\left(q\left(x_{t-1}\mid x_t,x_0\right)\Vert P_{\theta }\left(x_{t-1}\mid x_t\right)\right)\right]\end{array}\text{\hspace{1em}(30)}$$
其中，$KL\left(q\left(x_T\mid x_0\right)\Vert P\left(x_T\right)\right)$项与神经网络$\theta$无关，可以忽略。${\mathrm{E}}_{q\left(x_1\mid x_0\right)}\left[\log P_{\theta }\left(x_0\mid x_1\right)\right]$项可以看做是对原始数据的重建，DDPM针对该项构建了一个离散化的分段积分累乘，有点类似基于分类目标的自回归(auto-regressive)学习，感兴趣的同学可以参考DDPM原文。

上式中的$q\left(x_{t-1}\mid x_t,x_0\right)$可以被转化为我们了解的处理方式
$$\begin{array}{rl}q\left(x_{t-1}\mid x_t,x_0\right)& =\frac{q\left(x_{t-1},x_t,x_0\right)}{q\left(x_t,x_0\right)}\\ & =\frac{q\left(x_t\mid x_{t-1}\right)q\left(x_{t-1}\mid x_0\right)q\left(x_0\right)}{q\left(x_t\mid x_0\right)q\left(x_0\right)}\\ & =\frac{q\left(x_t\mid x_{t-1}\right)q\left(x_{t-1}\mid x_0\right)}{q\left(x_t\mid x_0\right)}\end{array}\text{\hspace{1em}(31)}$$
为了计算$KL\left(q\left(x_{t-1}\mid x_t,x_0\right)\Vert P_{\theta }\left(x_{t-1}\mid x_t\right)\right)$，我们还需要将上式进行展开，但是展开的过程过于复杂，在此我们只取其结果，详细的推导过程可参考论文^[13]

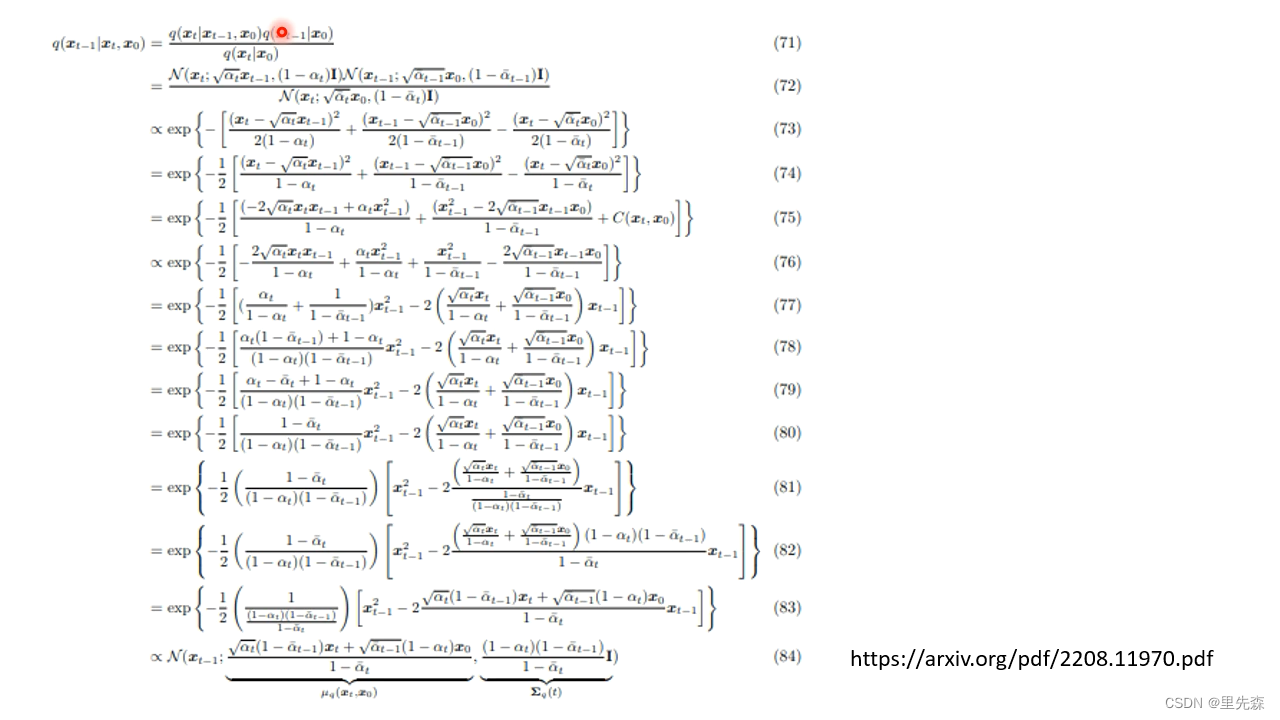
至此，我们可以知道$q\left(x_{t-1}\mid x_t,x_0\right)$这个分布的中值以及方差，这有助于我们计算$q\left(x_{t-1}\mid x_t,x_0\right)$与$P_{\theta }\left(x_{t-1}\mid x_t\right)$之间的KL散度。

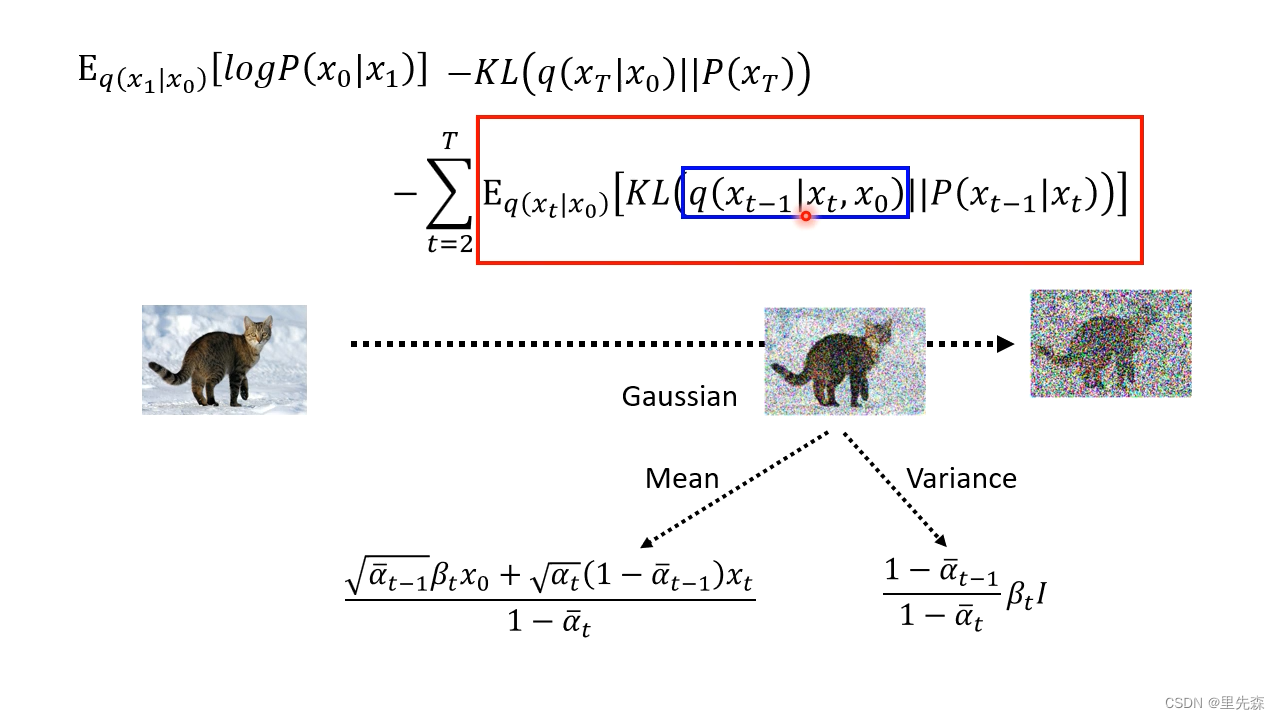
回到我们整体的下界公式中来，若要尽可能的提升我们$\log P_{\theta }(x_0)$的下界，我们需要使$KL\left(q\left(x_{t-1}\mid x_t,x_0\right)\Vert P_{\theta }\left(x_{t-1}\mid x_t\right)\right)$的值尽可能的小，也即是$q\left(x_{t-1}\mid x_t,x_0\right)$与$P_{\theta }\left(x_{t-1}\mid x_t\right)$之间的差异越小越好。对于$q\left(x_{t-1}\mid x_t,x_0\right)$，它是我们预先设定好的计算过程，方差与中值已经确定。$P_{\theta }\left(x_{t-1}\mid x_t\right)$与我们神经网络有关，在DDPM论文中为了简化讨论，假设神经网络输出的分布方差是固定的。因此，我们所能做的便是让$P_{\theta }\left(x_{t-1}\mid x_t\right)$的中值向$q\left(x_{t-1}\mid x_t,x_0\right)$的中值尽可能的靠近。已知$q\left(x_{t-1}\mid x_t,x_0\right)$的中值如下
$$\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0+\sqrt{{\alpha }_t}\left(1-{\bar{\alpha }}_{t-1}\right)x_t}{1-{\bar{\alpha }}_t}\text{\hspace{1em}(32)}$$
根据式(18)，我们有
$$x_0=\frac{x_t-\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_t}}{\sqrt{{\bar{\alpha }}_t}}\text{\hspace{1em}(33)}$$
代入式(32)，可得
$$\begin{array}{rl}\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0+\sqrt{{\alpha }_t}\left(1-{\bar{\alpha }}_{t-1}\right)x_t}{1-{\bar{\alpha }}_t}& =\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t\left(\frac{x_t-\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_t}}{\sqrt{{\bar{\alpha }}_t}}\right)+\sqrt{{\alpha }_t}\left(1-{\bar{\alpha }}_{t-1}\right)x_t}{1-{\bar{\alpha }}_t}\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}\overline{{ϵ}_t}\right)\end{array}\text{\hspace{1em}(34)}$$
在上式中，${\alpha }_t$类（${\beta }_t$）的都是预先已经定义好的超参数项，因此，神经网络实际需要预测的只有右侧的噪声项$\overline{{ϵ}_t}$。换句话说，当神经网络预测的噪声与实际噪声越接近，则$P_{\theta }(x_0)$下界将会越高，DDPM最终生成的图像也会越好。

2.3.4 *为何要添加噪声

单纯查看DDPM中sampling过程你可能会感到疑惑，为什么不能直接取模型输出的高斯分布中值作为结果，而是要在其上添加一个${\sigma }_{t}z$项。一方面来看，在2.3.1节中我们定义模型输出的实质上是高斯分布的中值，因此还需要对其添加一个${\sigma }_{t}z$项（作为方差项）以转换为高斯分布。另一方面，DDPM实质上是一个自回归的过程，在从$x_T$逐步去除噪声到$x_0$的过程中，每次得到的机率最大的结果并不一定就是最好的结果，不如将一次到位的想法改为多次到位。对每次神经网络得到的结果添加一个噪声，可以看作是为后续步骤添加可能性。