注:本文为“数学无字”相关文章合辑。
图片清晰度受引文原图所限。
略作重排,如有内容异常,请看原文。
数学无字证明:从几何到数列的直观演绎
无字证明(Proof Without Words, PWW)是一种仅通过图像展示,无需文字解释的数学证明方式。它在数学领域中独具魅力,通过其直观性与简洁性,以全新的视角理解数学的优雅和数学之美。
一、几何领域的无字证明
(一)三角函数恒等式的几何证明
- 正弦与余弦的平方和:通过单位圆的几何构造,直观展示 sin 2 θ + cos 2 θ = 1 \sin^2 \theta + \cos^2 \theta = 1 sin2θ+cos2θ=1。
- 正切与正割的关系:利用直角三角形的边长关系,证明 tan 2 θ + 1 = sec 2 θ \tan^2 \theta + 1 = \sec^2 \theta tan2θ+1=sec2θ。
- 两角和与差的三角函数公式:借助几何图形,展示 sin ( x ± y ) \sin(x \pm y) sin(x±y) 和 cos ( x ± y ) \cos(x \pm y) cos(x±y) 的推导过程,使复杂的三角函数关系变得一目了然。
(二)几何定理的无字证明
- 勾股定理:通过图形的拼接与组合,直观展示直角三角形的边长关系,呈现多种不同的证明方法。
- 余弦定理:将勾股定理推广到任意三角形,利用几何图形展示其证明过程,揭示三角形边长与夹角之间的内在联系。
- 多边形外角和:通过动态演示或静态图形,展示多边形外角和恒为 360° 的几何原理,使抽象的定理变得直观易懂。
(三)几何图形的面积与体积关系
- 圆的面积与周长:利用圆的分割与拼接,展示圆的面积公式 A = π r 2 A = \pi r^2 A=πr2 的几何推导过程,同时揭示圆的面积与周长之间的关系。
- 立方体与长方体的体积关系:通过几何图形的组合与分解,直观展示立方体与长方体体积之间的转换关系,为理解三维空间中的体积计算提供新的视角。
- 旋轮线下的面积:借助物理实验(例如滚动圆)与几何构造,展示旋轮线下的面积等于对应圆面积的三倍,将数学与物理相结合,呈现独特的证明思路。
二、数列与代数的无字证明
(一)数列的性质与求和公式
- 斐波那契数列的恒等式:通过几何图形的排列与组合,直观展示斐波那契数列的性质与相关恒等式,如 F n + 1 F n − 1 − F n 2 = ( − 1 ) n F_{n+1} F_{n-1} - F_n^2 = (-1)^n Fn+1Fn−1−Fn2=(−1)n,使数列的规律更加清晰。
- 等差数列与等比数列的求和:利用几何图形的堆叠与排列,展示等差数列与等比数列的求和公式,使复杂的代数公式变得直观易懂。
- 平方数与立方数的求和公式:通过几何图形的构造,直观展示平方数与立方数的求和公式,如 1 2 + 2 2 + ⋯ + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 1^2 + 2^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6} 12+22+⋯+n2=6n(n+1)(2n+1),呈现数列求和的几何意义。
(二)代数恒等式的几何证明
- 二项式定理:借助几何图形的组合与排列(例如杨辉三角的几何解释),展示二项式定理的展开过程,使复杂的代数公式变得直观易懂。
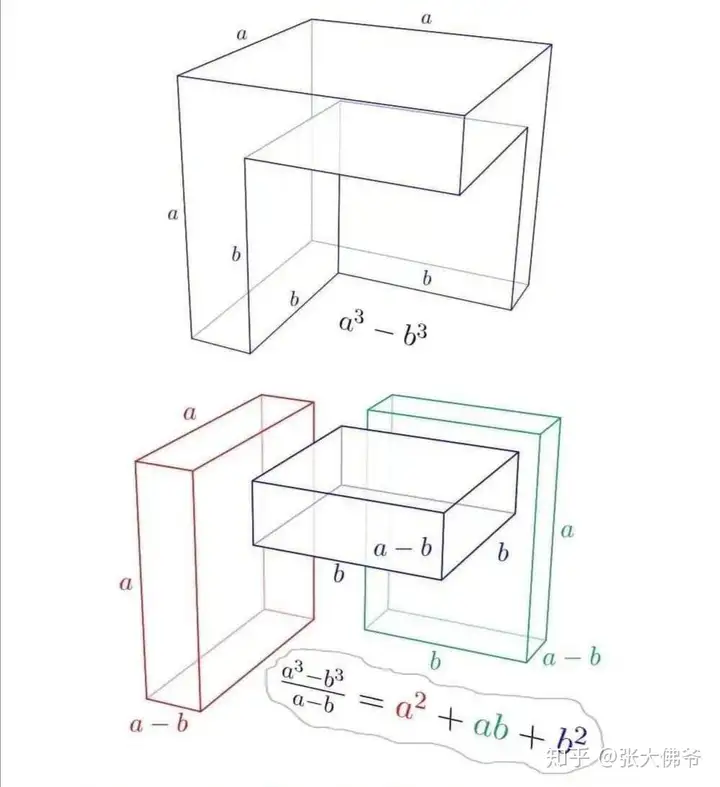
- 平方差与立方差公式:通过几何图形的构造,直观展示平方差公式 a 2 − b 2 = ( a + b ) ( a − b ) a^2 - b^2 = (a + b)(a - b) a2−b2=(a+b)(a−b) 与立方差公式 a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a^3 - b^3 = (a - b)(a^2 + ab + b^2) a3−b3=(a−b)(a2+ab+b2),呈现代数恒等式的几何意义。
- 均值不等式:利用几何图形的面积或长度关系,展示算术平均数、几何平均数、调和平均数之间的不等关系,使抽象的不等式变得直观易懂。(例如,用直角梯形的面积关系证明算术平均数大于等于几何平均数)
三、函数与微积分的无字证明
(一)函数性质的几何展示
- 三角函数的导数:通过几何图形的动态演示,或者通过单位圆上的点的运动,直观展示 sin x \sin x sinx 和 cos x \cos x cosx 的导数关系,使复杂的函数求导过程变得直观易懂。
- 指数函数与对数函数的性质:利用几何图形的变换,展示指数函数与对数函数的单调性、对称性等性质,呈现函数之间的内在联系。(例如,通过图像的对称性展示互为反函数的关系)
- 泰勒展开的几何意义:借助几何图形的逼近与拟合,展示函数的泰勒展开过程,使复杂的级数展开变得直观易懂。(例如用多项式函数逼近曲线)
(二)微积分定理的无字证明
- 分部积分公式:通过几何图形的面积分割与组合,直观展示分部积分公式的推导过程,使复杂的积分计算变得直观易懂。
- 微积分基本定理:利用几何图形的面积与曲线的关系,展示微积分基本定理的几何意义,呈现积分与导数之间的内在联系。
- 极限的几何证明:通过几何图形的逼近与极限过程,直观展示一些常见极限的证明过程,使抽象的极限概念变得直观易懂。(例如,夹逼定理的几何解释)
数学中有哪些漂亮的无字证明?
吴大锤 知乎日报
无字证明(Proof Without Words)是指仅用图像而无需文字解释就能不证自明的数学命题。由于其不证自明的特性,这种证明方式被认为比严格的数学证明更为优雅与有条理。
In mathematics, a proof without words is a proof of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than more formal and mathematically rigorous proofs due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable。
以下是一些无字证明的例子:
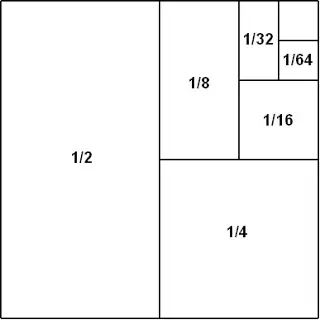
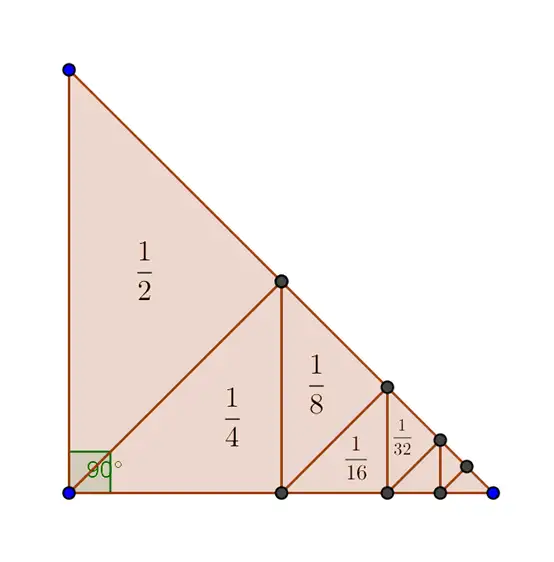
1. 证明 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 + ⋯ = 1 \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\dots=1 21+41+81+161+321+641+⋯=1
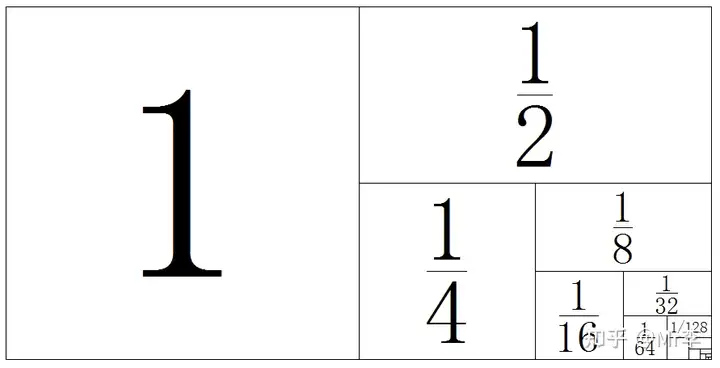
2. sin 2 θ + cos 2 θ = 1 \sin^2 \theta + \cos^2 \theta = 1 sin2θ+cos2θ=1 的几何证明,图中是一个四分之一的单位圆
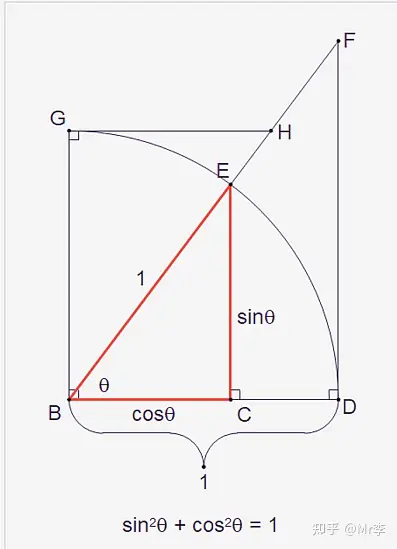
3. tan 2 θ + 1 = sec 2 θ \tan^2 \theta + 1 = \sec^2 \theta tan2θ+1=sec2θ 的几何证明
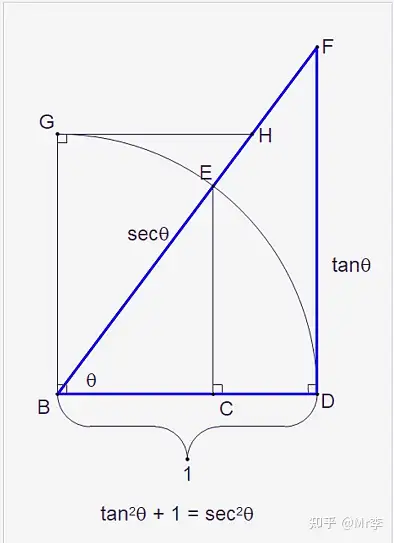
4. cot 2 θ + 1 = csc 2 θ \cot^2 \theta + 1 = \csc^2 \theta cot2θ+1=csc2θ
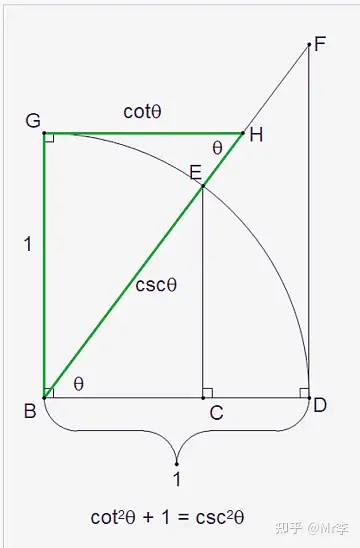
5. 两角之和的正弦 sin ( x + y ) \sin(x+y) sin(x+y) 和余弦 cos ( x + y ) \cos(x+y) cos(x+y) 的几何证明
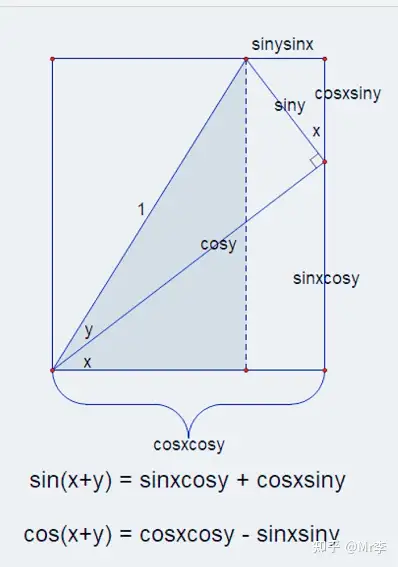
6. 两角之差的正弦 sin ( x − y ) \sin(x-y) sin(x−y) 和余弦 cos ( x − y ) \cos(x-y) cos(x−y) 的几何证明
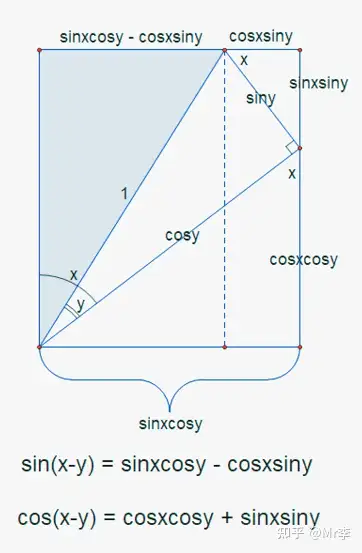
7. 单位圆中的正弦 sin ( x + y ) \sin(x+y) sin(x+y) 和余弦 cos ( x + y ) \cos(x+y) cos(x+y) 的几何证明
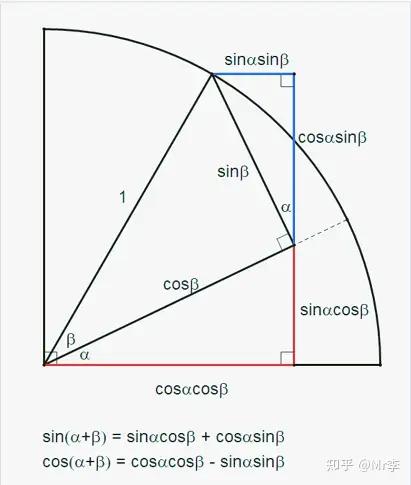
8. 正弦二倍角公式 sin 2 θ = 2 sin θ cos θ \sin 2\theta = 2 \sin \theta \cos \theta sin2θ=2sinθcosθ 的几何证明
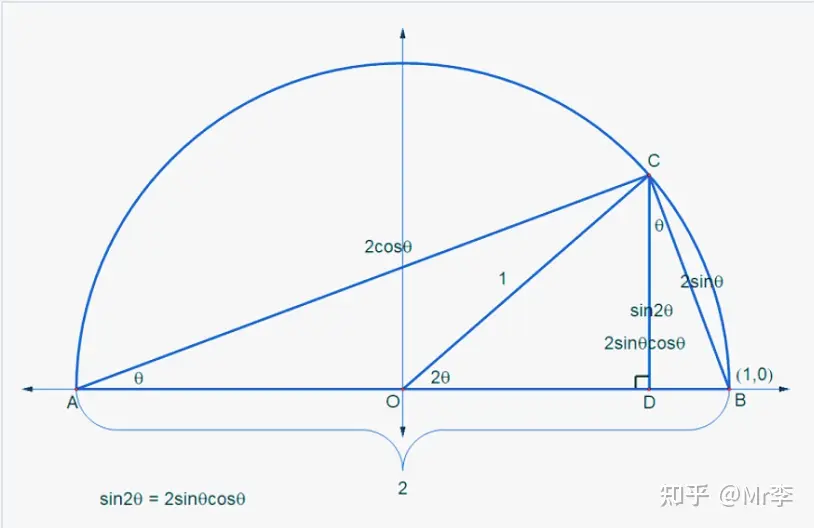
9. 余弦二倍角公式 cos 2 θ = 2 cos 2 θ − 1 \cos 2\theta = 2 \cos^2 \theta - 1 cos2θ=2cos2θ−1 的几何证明
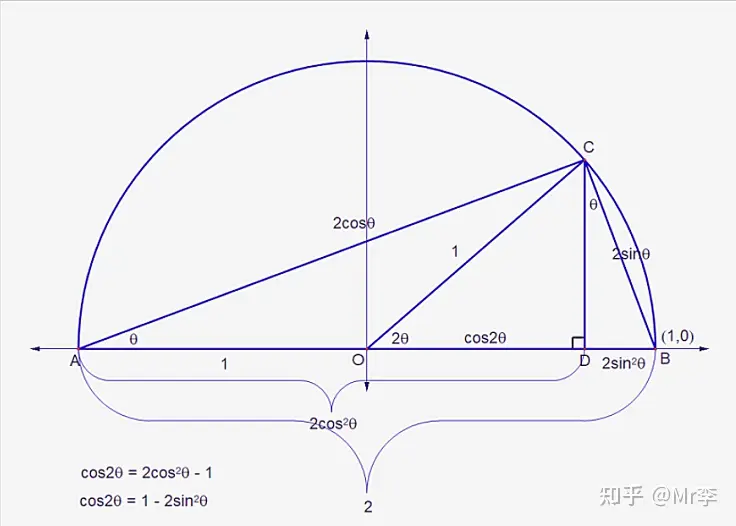
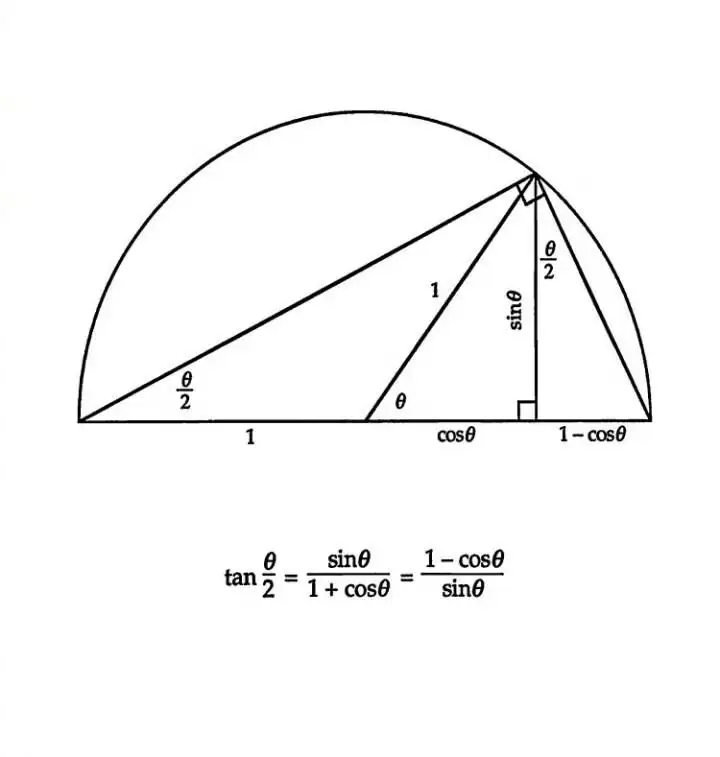
10. 正切半倍角 tan θ 2 \tan \frac{\theta}{2} tan2θ 的几何证明
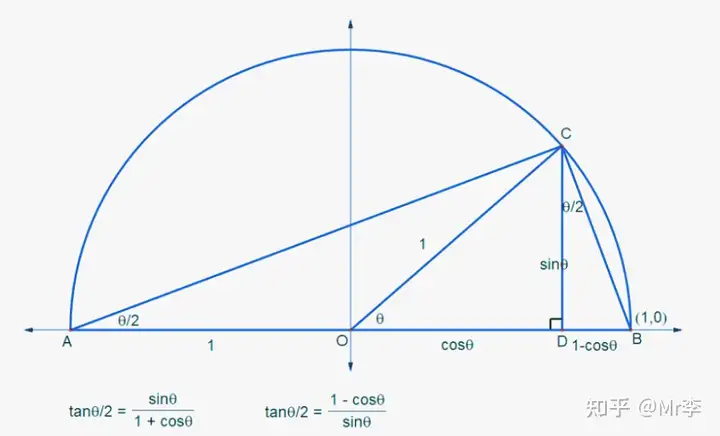
11. 余弦半倍角 cos θ 2 \cos \frac{\theta}{2} cos2θ 的几何证明
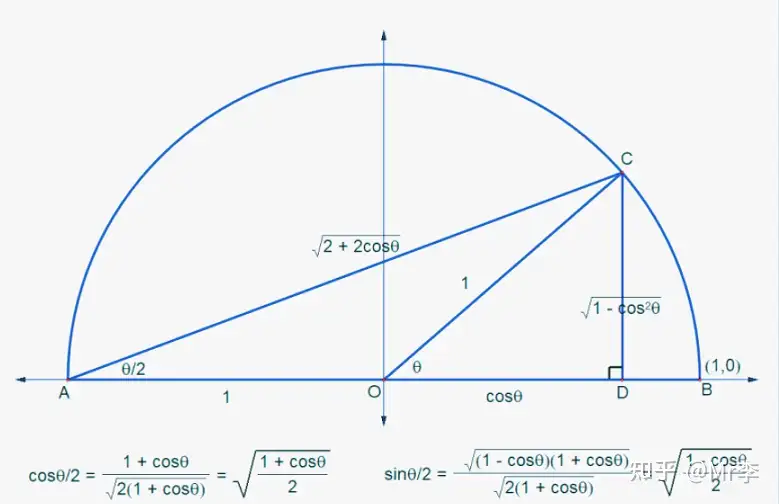
12. A sin X + B cos X A \sin X + B \cos X AsinX+BcosX 等式的几何证明
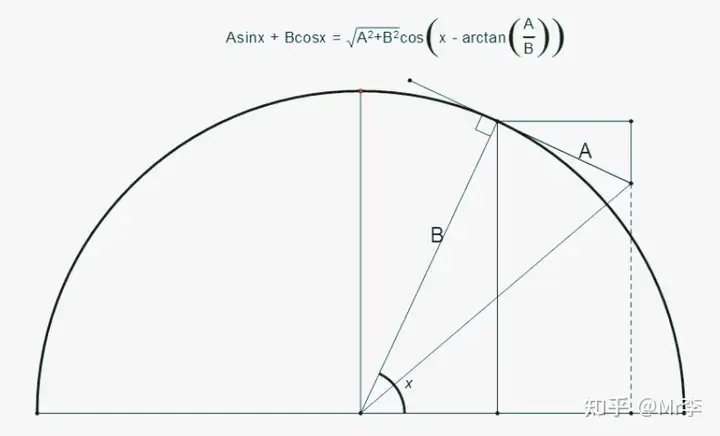
13. 两角之和正切 tan ( X + Y ) \tan(X+Y) tan(X+Y) 的几何证明
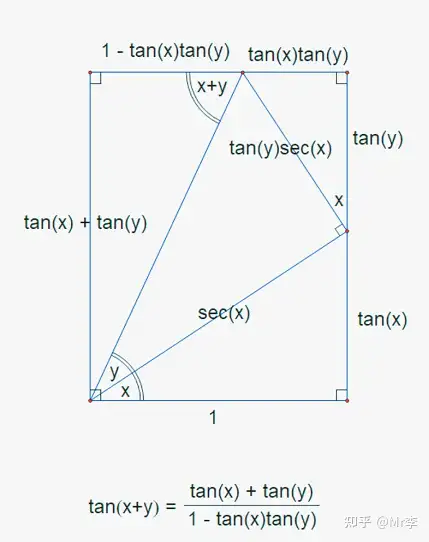
14. 两角之差正切 tan ( X − Y ) \tan(X-Y) tan(X−Y) 的几何证明
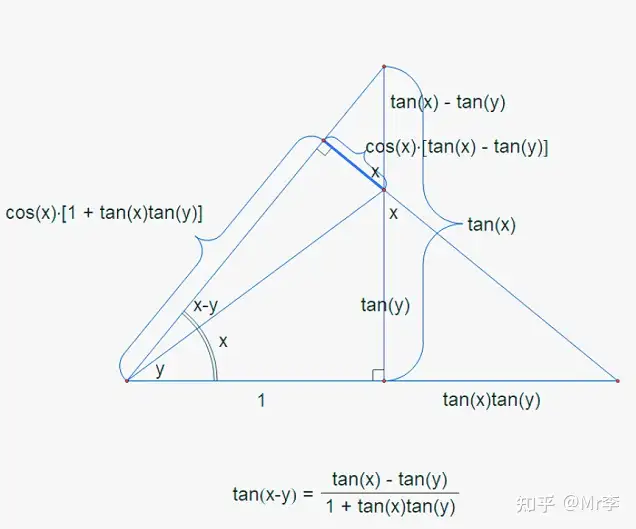
15. 斐波那契数列的恒等式
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21……这个数列从第三项开始,每一项都等于前两项之和,即 F n + 1 = F n + F n − 1 F_{n+1} = F_n + F_{n-1} Fn+1=Fn+Fn−1。它的通项公式是
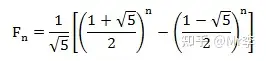
有趣的是,这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。而且当 n n n 无穷大时, F n − 1 F n \frac{F_{n-1}}{F_n} FnFn−1 越来越逼近黄金分割数 0.618。正因为它的种种神奇性质,美国数学会甚至从1960年代起出版了《斐波纳契数列》季刊。关于斐波那契数列,有一个恒等式是这样的。
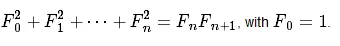
这个等式很漂亮,不需要借助复杂的数学推导,它有一个很直观的证明方法。
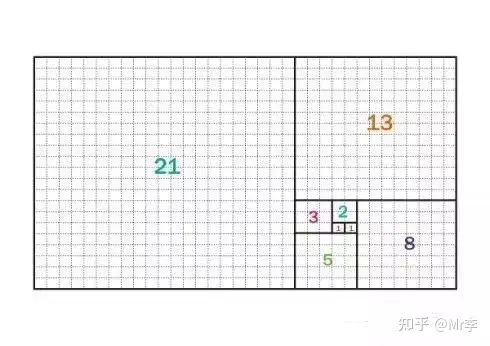
16. 勾股定理
这个大家小学就学过的古老定理,有着无数传奇故事。路明思(Elisha Scott Loomis)在 [毕达哥拉斯命题](Pythagorean Proposition)提到这个定理的证明方式居然有367种之多,实在让人惊讶。这里给出一个不需要语言的证明方法。

实际上勾股定理是 [余弦定理] 的一种特殊情况,而余弦定理的证明,同样可以不用语言。
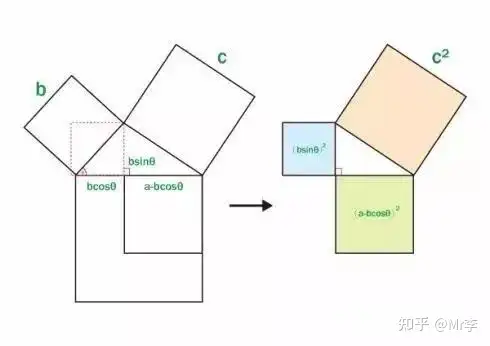
17. 关于 反正切的恒等式
关于反正切,有如下两个很精彩的等式:
arctan \frac{1}{2} + arctan \frac{1}{3} = \frac{\pi}{4}
arctan 1 + arctan 2 + arctan 3 = \pi
它们的证明方法也同样精彩。
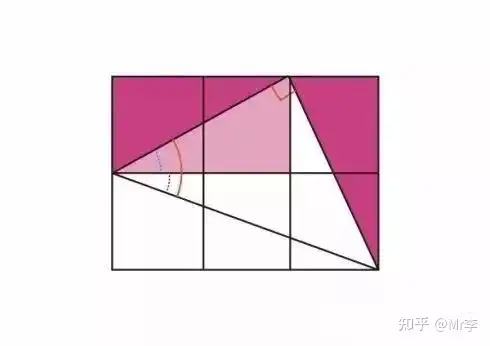
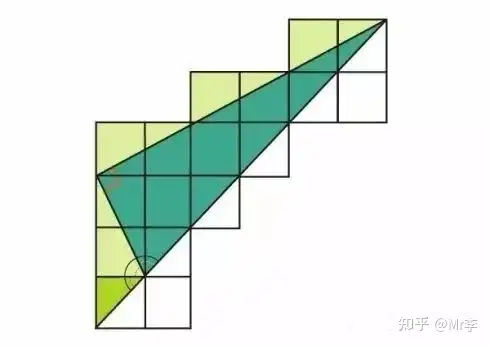
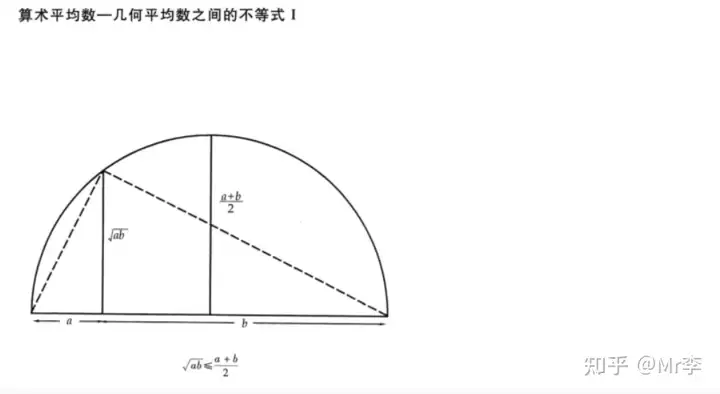
18. 几何平均值小于 算术平均值
这是不等式中最重要和基础的等式:
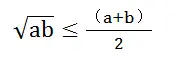
它也可以通过图形来证明。
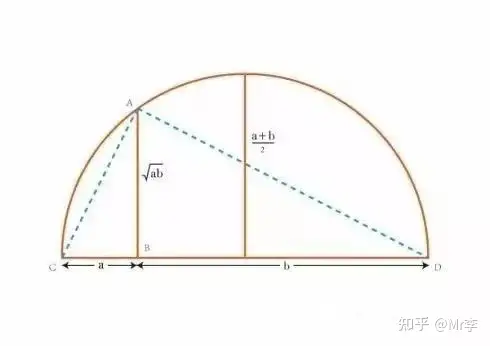
注意到 △ A B C ∼ △ D B A \triangle ABC \sim \triangle DBA △ABC∼△DBA,可以很轻松地得到 A B = a b AB = \sqrt{ab} AB=ab。剩下的就显而易见了。
19. 奇数的求和公式
这是奇数的求和公式,下图是当 n = 8 n = 8 n=8 时的情形

20. 平方数的求和公式
一个很漂亮的公式,证明的过程令人眼前一亮。
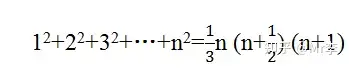
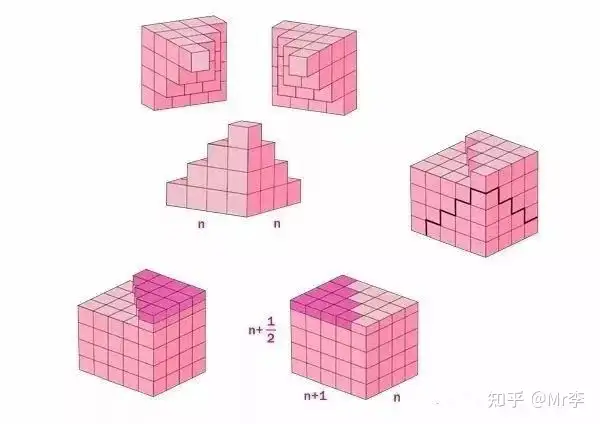
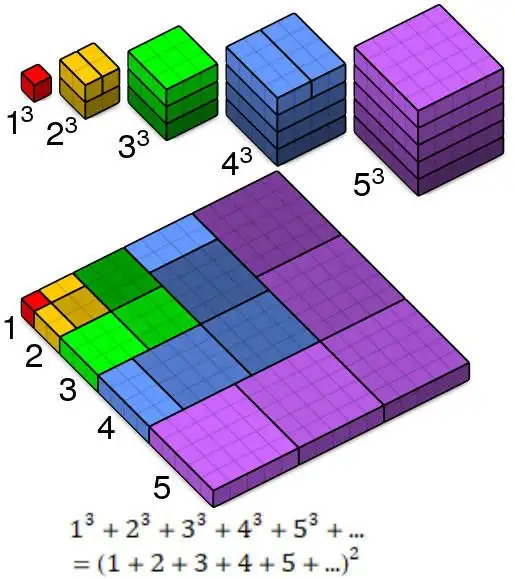
21. 立方数的求和公式
立方数的求和证明与平方数的求和证明方法有些相像:
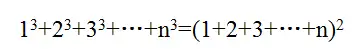
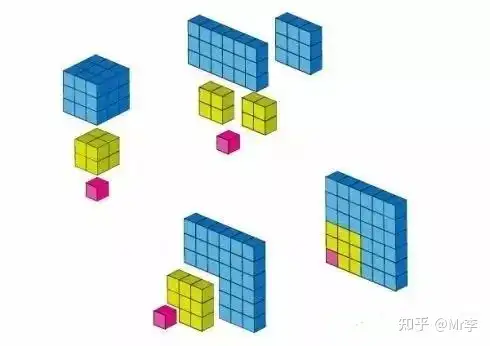
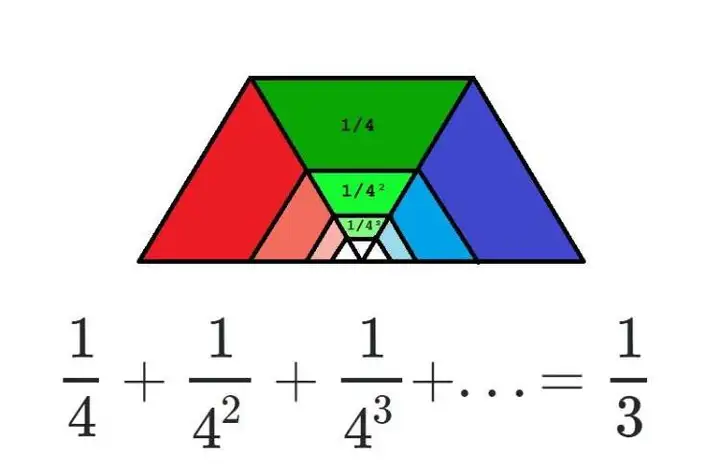
22. 结果为 1 3 \frac{1}{3} 31 的一组分子式
下面是一组分子式,它们的结果都等于 1 3 \frac{1}{3} 31 :
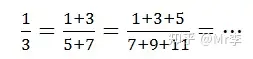
让我们用若干个小球看待这个公式。
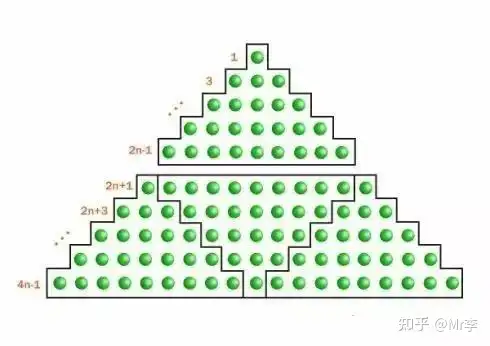
23. 最受数学家喜爱的无字证明
1989 年的《美国数学月刊》(American Mathematical Monthly)上有一个貌似非常困难的数学问题:下图是由一个个小三角形组成的正六边形棋盘,现在请你用右边的三种(仅朝向不同的)菱形把整个棋盘全部摆满(图中只摆了其中一部分),证明当你摆满整个棋盘后,你所使用的每种菱形数量一定相同。
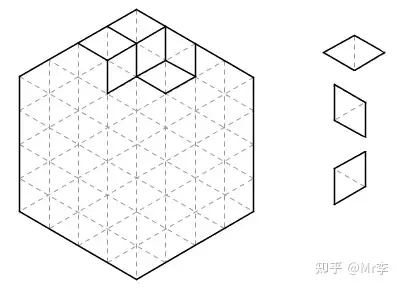
《美国数学月刊》提供了一个非常帅的“证明”。把每种菱形涂上一种颜色,整个图形瞬间有了立体感,看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面,它们的数目显然应该相等。
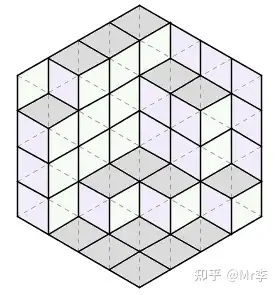
它把一个纯组合数学问题和立体空间图形结合在了一起,实在让人拍案叫绝。这个问题及其鬼斧神工般的“证明”流传甚广,深受数学家们的喜爱。死理性派曾经讨论过这个问题。同时它还是死理性派 logo 的出处。
24. 棋盘上的数学证明
在一个 8 × 8 8 \times 8 8×8 的国际象棋棋盘上,我们可以用 32 张多米诺骨牌(是两个相连正方形的长方形牌)覆盖整个棋盘上的 64 个方格。如果将对角线上的两个方格切掉,剩下来的 62 个格子还能用 31 张骨牌覆盖住吗?

答案是不能的。每一张骨牌在棋盘上必是覆盖住两个相邻方格,一白一黑。所以 31 张骨牌应该可以盖住 31 个黑格和 31 个白格。而这被切了角的棋盘上的方格有 32 个是一种颜色,另一种颜色是 30 个,因此是不能被 31 张骨牌覆盖的。
但是如果我们切掉的不是颜色相同的两个呢?假如我们从棋盘的任何部位切掉两个颜色不同的方格,那么剩下来的 62 格是否一定能被 31 张骨牌完全盖住?我可以告诉你这是一定能做到的,并且关于这个结论,存在一个非常漂亮的证明。建议读者在继续往下阅读前,可以先自行思考如何证明这个结论。

上图就是那个漂亮的证明。不妨对它再赘述两句。粗黑线条将整个棋盘转变为一条首尾相连、黑白格相间的封闭路线。从这棋盘上切掉任何两个颜色不同的方格,会让这个封闭线路变成两段线路(如果切掉的方格是相连的,那就是一条线路)。在这两段(或一段)线路中,两种颜色的格子数量都是偶数,故分别都可以被若干张骨牌覆盖。从而证明整个棋盘可以被 31 张骨牌完全覆盖。
这个著名的棋盘问题是数学游戏大师马丁·加德纳提出的,而上述精妙绝伦的证明则是数学家哥莫瑞(Ralph Gomory)找到的。它们后来被收录在《意料之外的绞刑和其他数学娱乐》这本书里。
25. 自然数求和公式
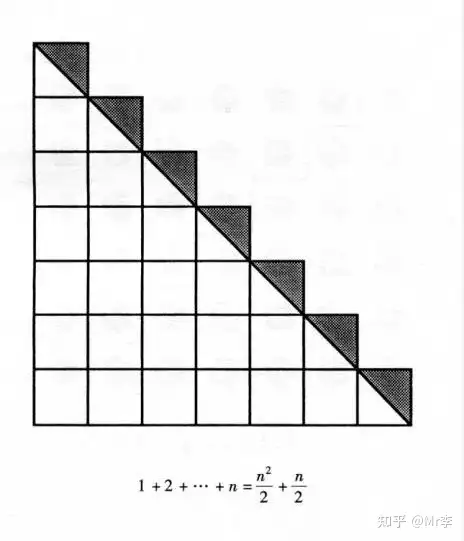
26. 自然数阶梯求和与平方和的关系

27. 算术平均数——几何平均数之间的不等式
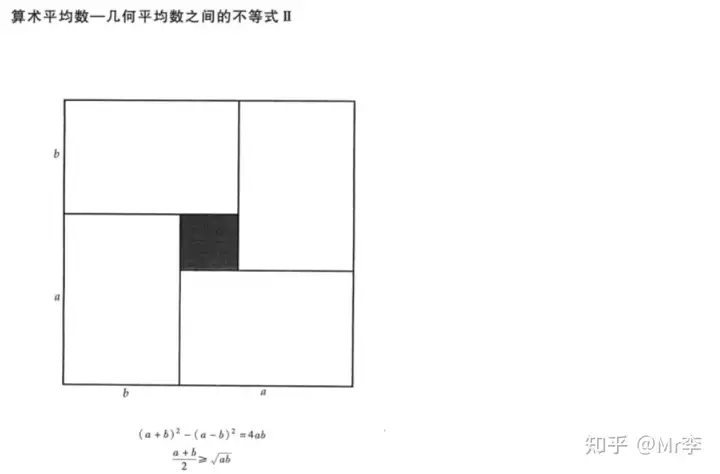
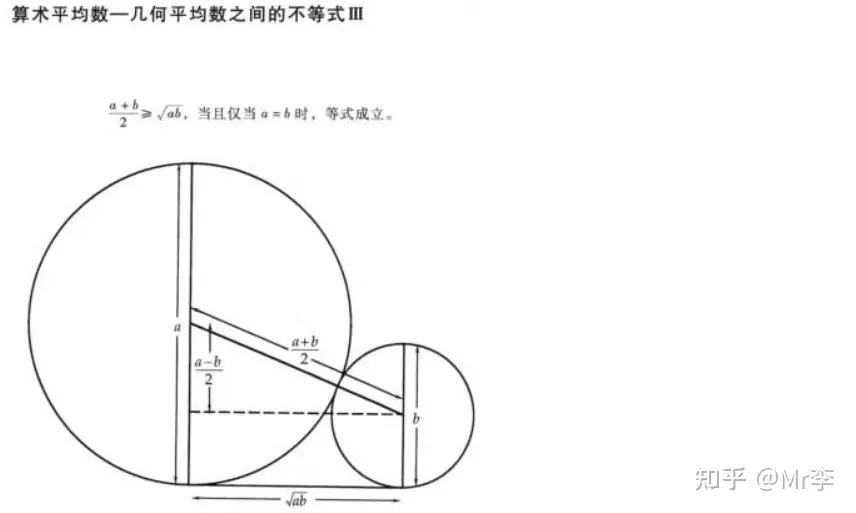
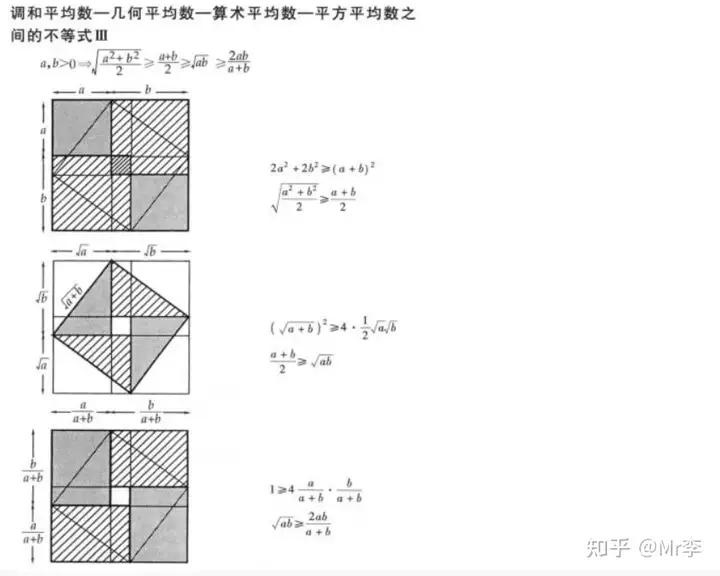
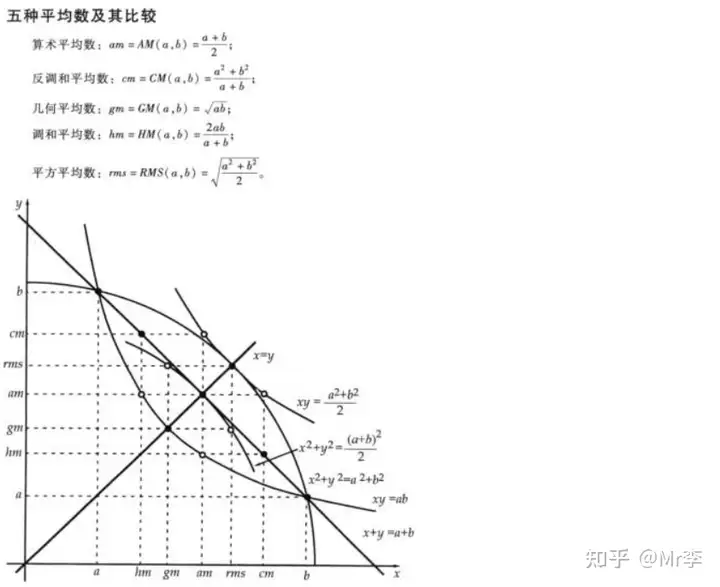
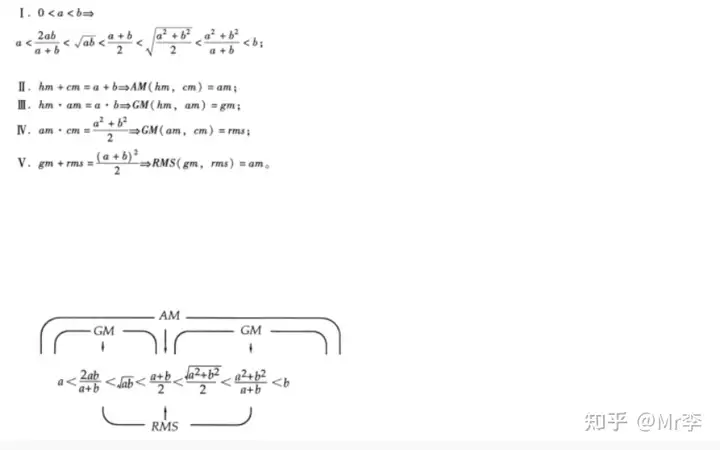
28. 调和平均数——几何平均数——算术平均数——平方平均数之间的不等式
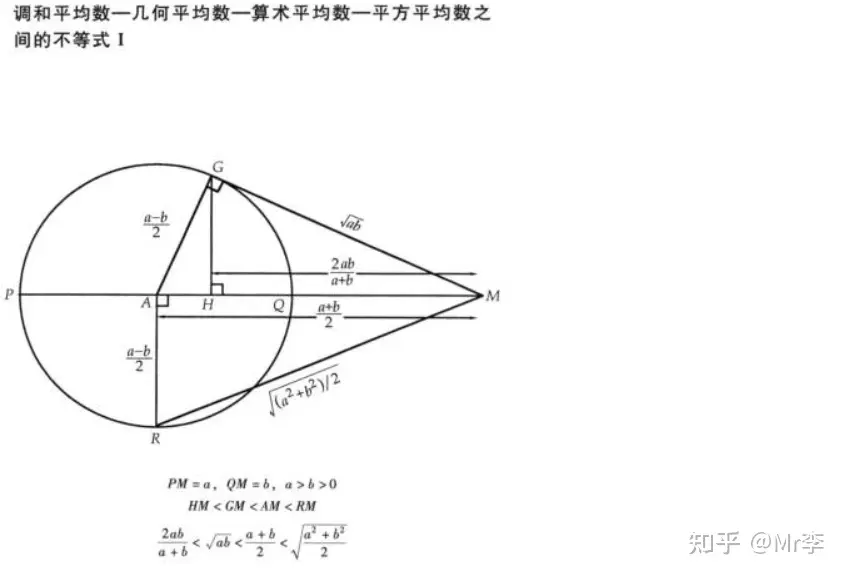
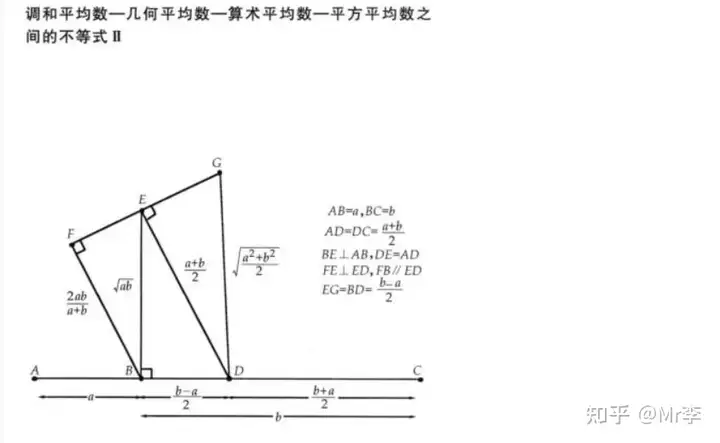
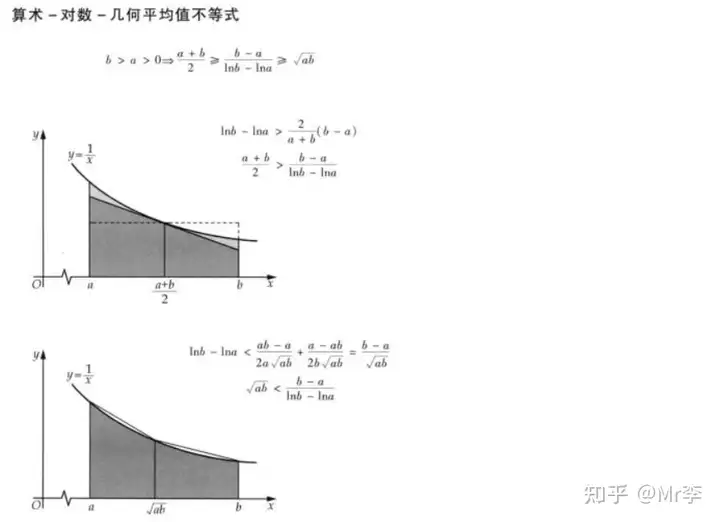
29. 算术 - 对数 - 几何平均值不等式
30. 单调数列的切比雪夫不等式
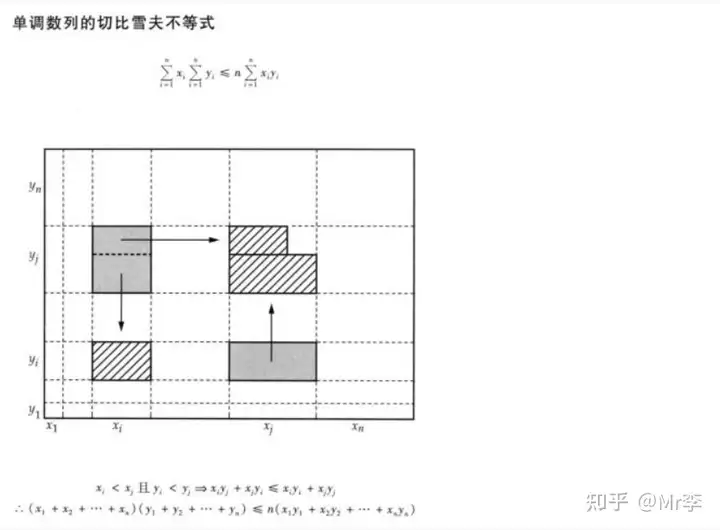
31. 用注水实验法验证勾股定理
-
取直角三角形的三边长 a , b , c a, b, c a,b,c,其中 c c c 为斜边,分别制作成底面边长为 a , b , c a, b, c a,b,c 的正方形,高度相等的长方体容器;
-
将底面边长为 a , b a, b a,b 的正方体容器注满水,再将两个容器中的水倒入底面边长为 c c c 的容器中;
-
奇迹发生了,两个容器中的水恰好可以注满第三个容器!

32. 5 = 31.5?
这是一个非常经典的视觉错误,已被作者 Trekky0623 公之于众,很快风靡于世界。

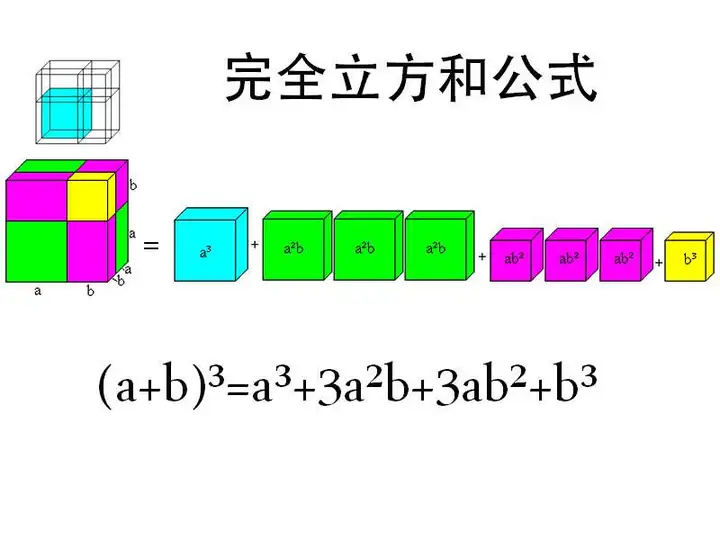
立方和公式

( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 (a+b)3=a3+3a2b+3ab2+b3
立方差公式
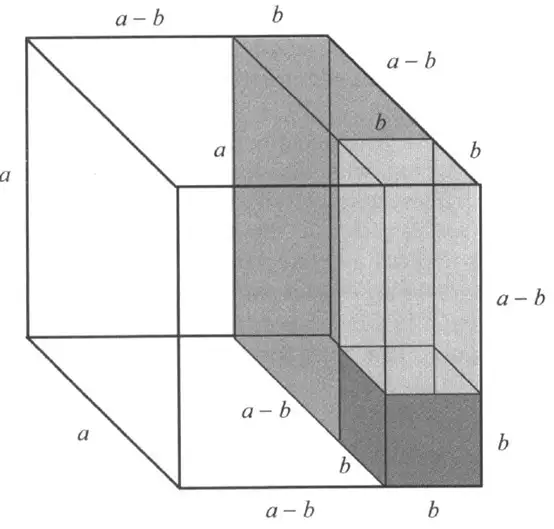
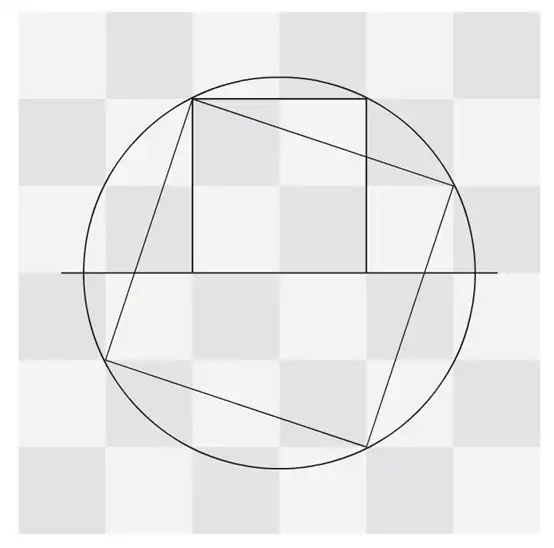
半圆和圆中的正方形
证明半径相同的圆和半圆中,半圆的内接正方形面积是圆内接正方形面积的 2 5 \frac{2}{5} 52。

证明:
利用圆的周长公式证明面积公式
参考文献:Steven Strogatz’s column:
http://opinionator.blogs.nytimes.com/2010/04/04/take-it-to-the-limit/
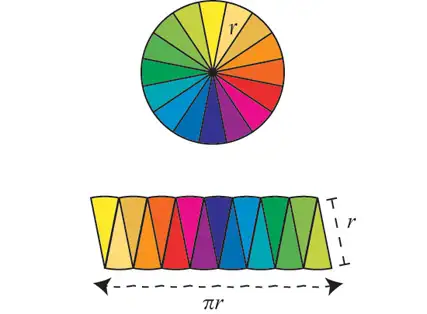
逐步的分割过程:
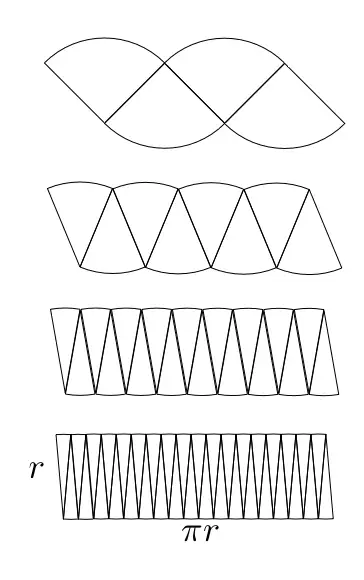
面积平分
将直角三角形中的直角二等分的线也将斜边上的正方形一分为二。
source: https://www.futilitycloset.com/2011/09/12/half-and-half/

证明如下:

旋轮线的面积
车轮在地上旋转一圈的过程中,车轮圆周上的某一点划过的曲线就叫做“旋轮线”。不过,在没有微积分的时代,计算曲线下方的面积几乎是一件不可能完成的任务。伽利略是如何求出旋轮线下方的面积的呢?他的方法简单得实在是出人意料:他在金属板上切出旋轮线的形状,拿到秤上称了称,发现重量正好是对应的圆形金属片的三倍。
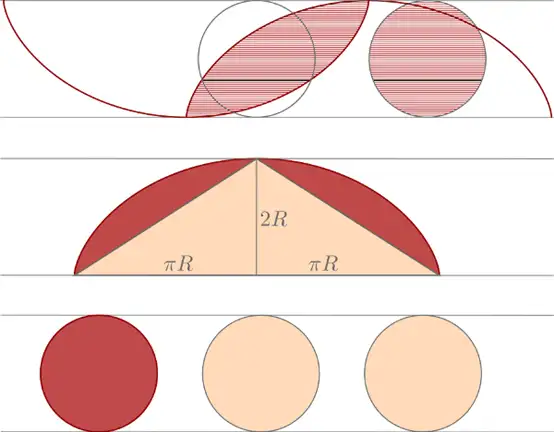
求极限
求证:

证明:
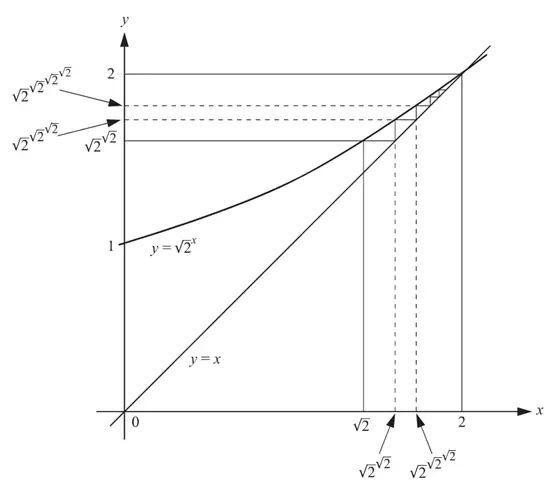

参考文献:http://www.cecm.sfu.ca/~loki/Papers/Numbers/ (Visible Structures in Number Theory, by Peter Borwein and Loki Jorgenson, The American Mathematical Monthly, vol. 108, no. 5, 2002, pp. 897-910)
还有另外一种证明方式:
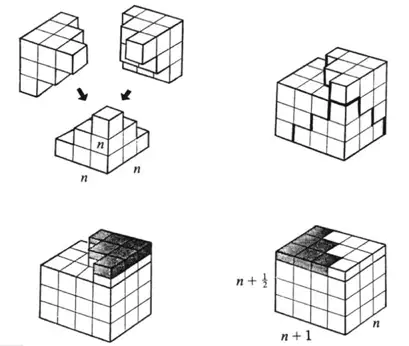
求平方和
(Author: Man-Keung Siu)
非常初等的知识,但是我最喜欢:
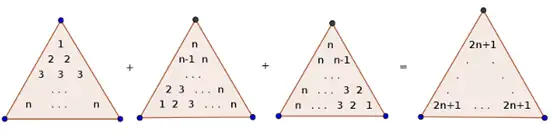
另一种证明方法:
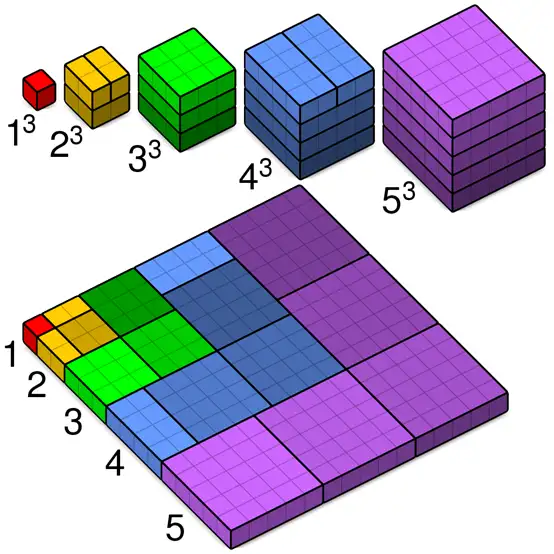
求立方和
斐波那契数列的恒等式
斐波那契数列:1、1、2、3、5、8、13、21……其递推公式为 F n + 1 = F n + F n − 1 F_{n+1} = F_n + F_{n-1} Fn+1=Fn+Fn−1。关于斐波那契数列,有一个漂亮的恒等式:
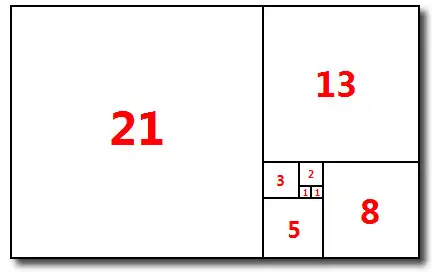
斐波那契数列与反三角函数的巧合
斐波那契数列是如下的一串数字:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,……
然而更神奇的现象在这里:
第一种关系表明,斜率为 1 2 \frac{1}{2} 21 的直线倾斜角与斜率为 1 3 \frac{1}{3} 31 的直线倾斜角的和为斜率为 1 的直线的倾斜角。下面是一种无字证明:
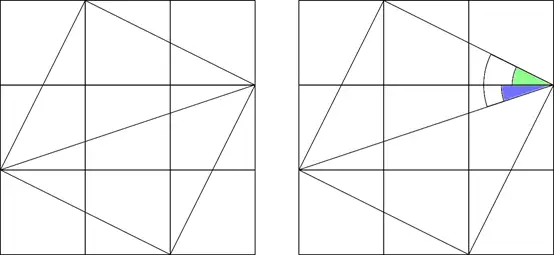
两角和与差的正弦公式
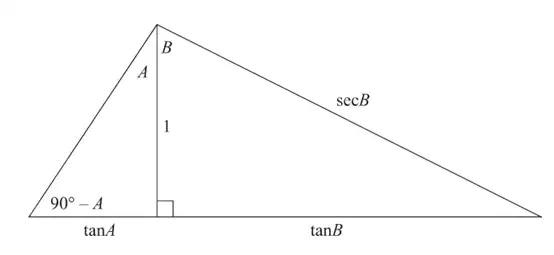
另一种证明:
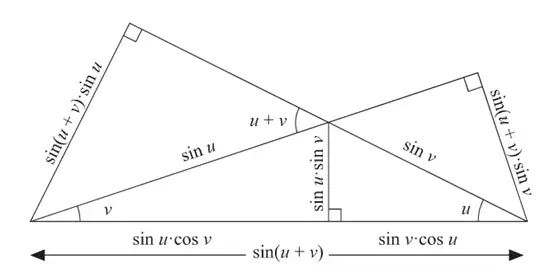
两角和与差的余弦公式
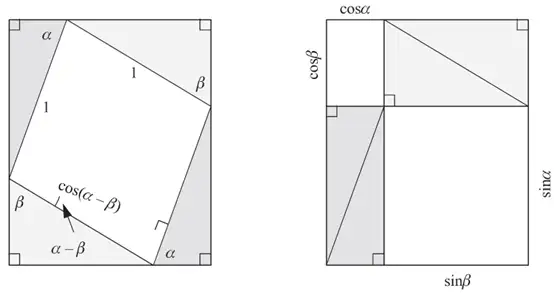
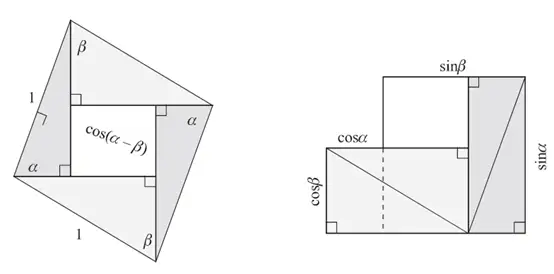
sin x \sin x sinx 求导为 cos x \cos x cosx
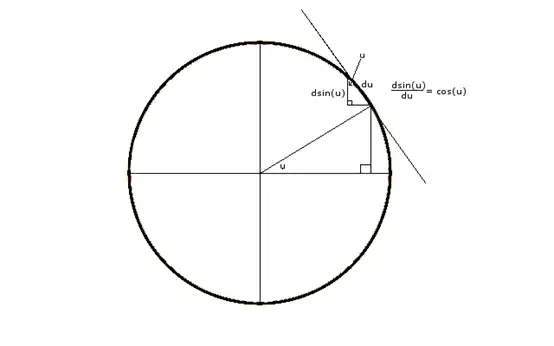
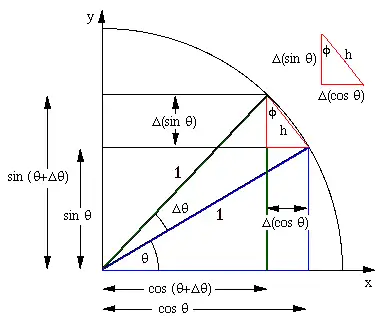
参考文献:http://www.animations.physics.unsw.edu.au/jw/calculus.htm#Trigonometric
分部积分公式(Integration by Parts)
(Got from: Roger B. Nelsen, Proof without Words: Integration by Parts, Mathematics Magazine, Vol. 64, No. 2 (Apr., 1991), p. 130; the original link is http://www.maa.org/sites/default/files/Roger_B04151._Nelsen.pdf.)
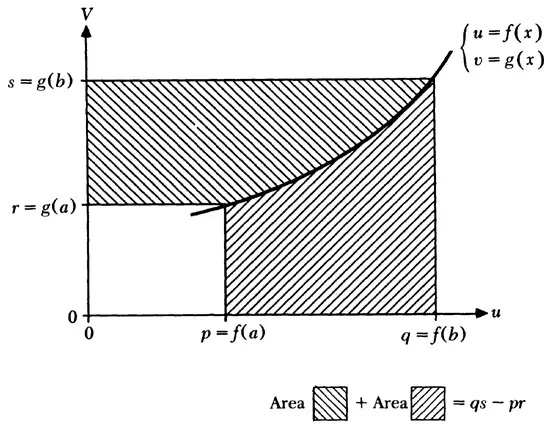
∫ r s u d v + ∫ p q v d u = u v ∣ ( p , r ) ( q , s ) ∫ a b f ( x ) g ′ ( x ) d x = f ( x ) g ( x ) ∣ a b − ∫ a b g ( x ) f ′ ( x ) d x \begin{array}{l} \int_{r}^{s} u \, dv + \int_{p}^{q} v \, du = u v \Big|_{(p,r)}^{(q,s)} \\ \int_{a}^{b} f(x) g'(x) \, dx = f(x) g(x) \Big|_{a}^{b} - \int_{a}^{b} g(x) f'(x) \, dx \end{array} ∫rsudv+∫pqvdu=uv (p,r)(q,s)∫abf(x)g′(x)dx=f(x)g(x) ab−∫abg(x)f′(x)dx
均值不等式

证明:
x 3 3 + y 3 3 + z 3 3 ≥ x y z \frac{x^3}{3} + \frac{y^3}{3} + \frac{z^3}{3} \geq x y z 3x3+3y3+3z3≥xyz
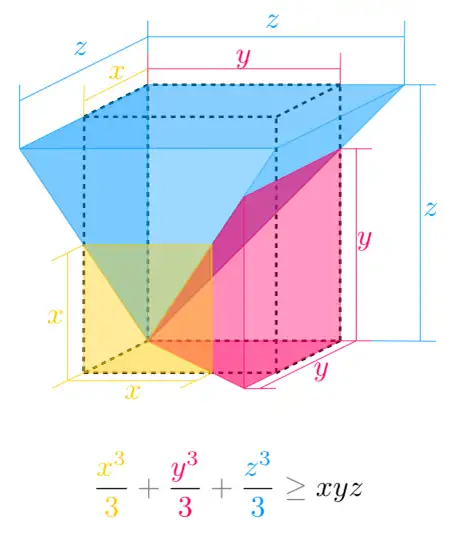
参考文献:美国数学家 Roger B. Nelson 所主编的 Proofs without Words
二倍角公式与半角公式
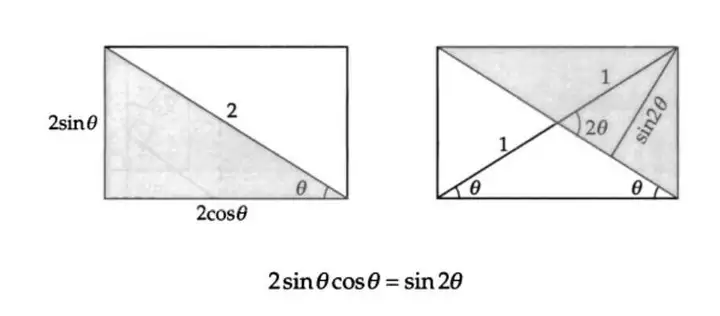
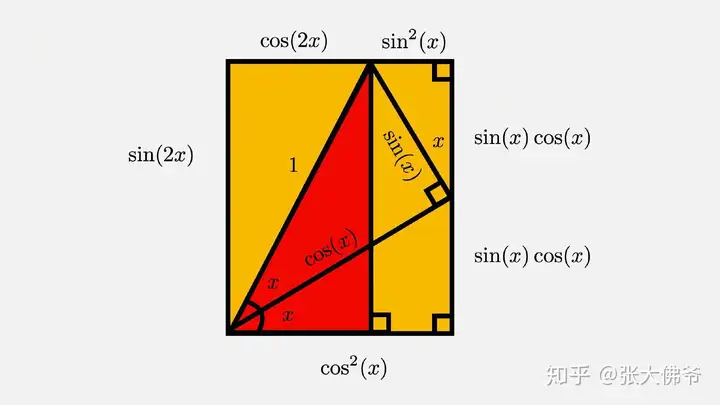
和角公式
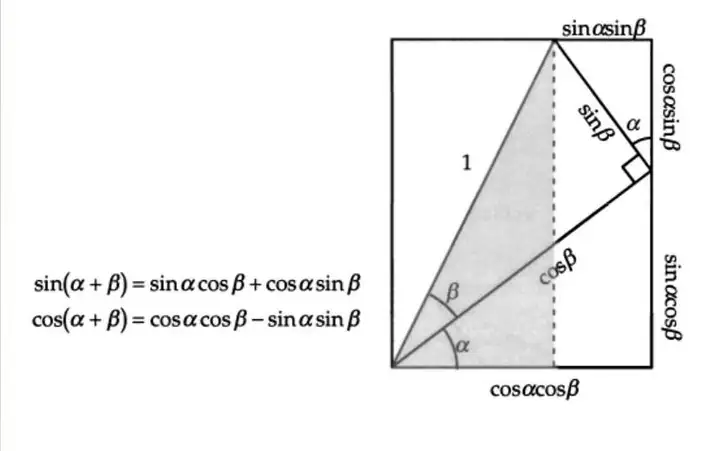
平方求和
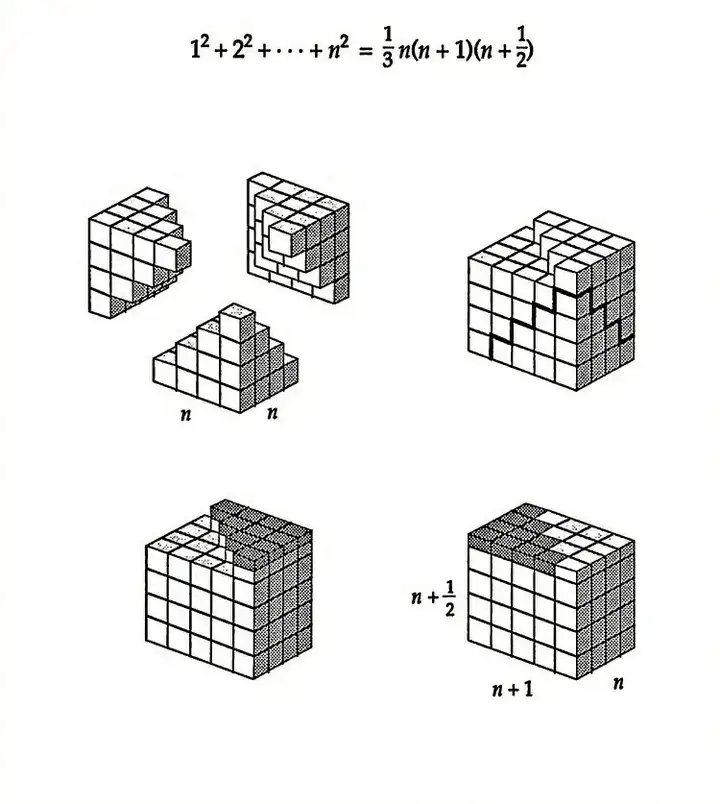
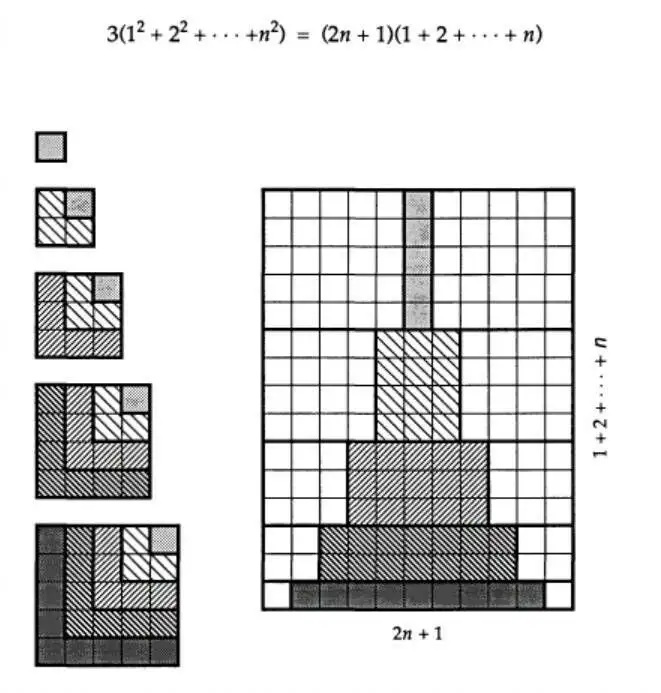
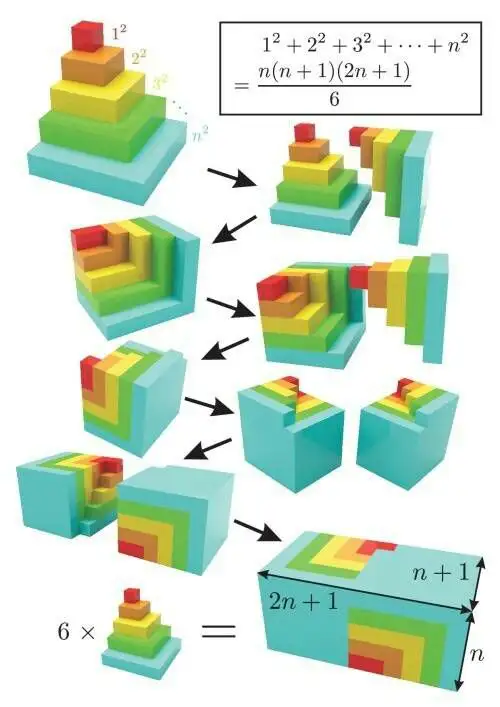
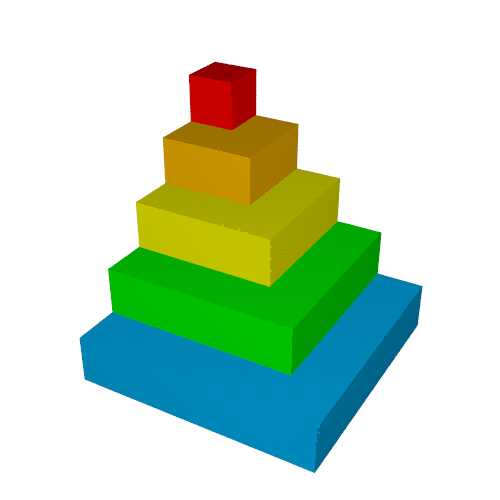
立方求和
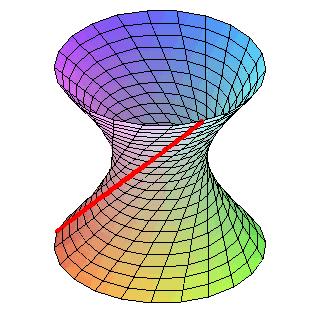
曲面可以完全由直线构成


勾股定理
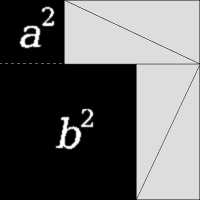
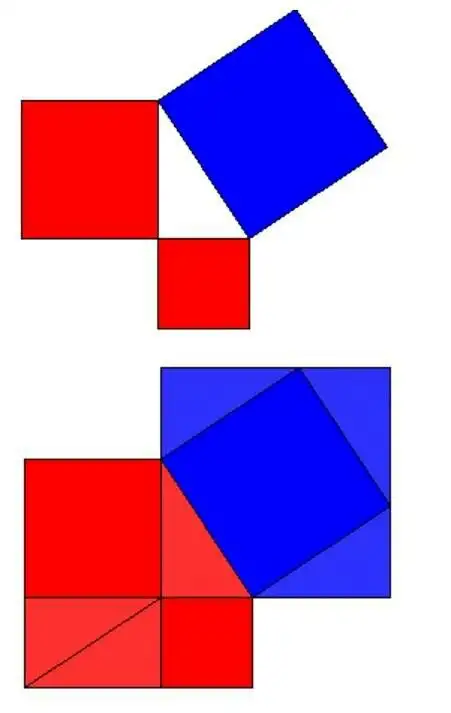
求和级数展开
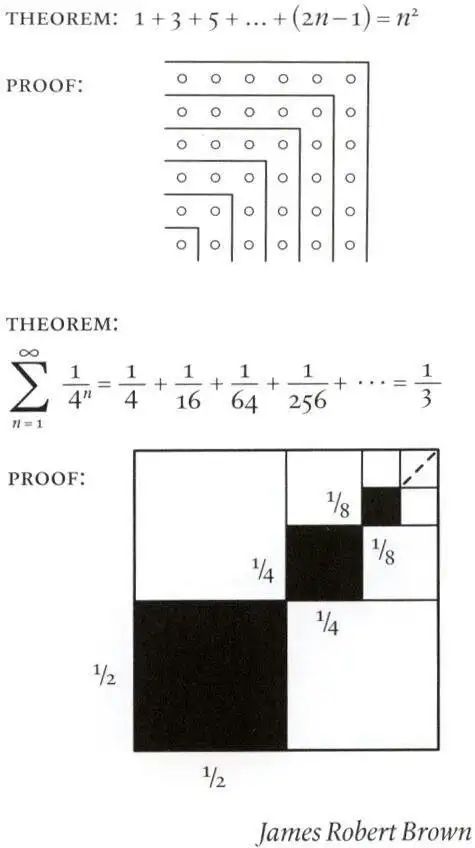
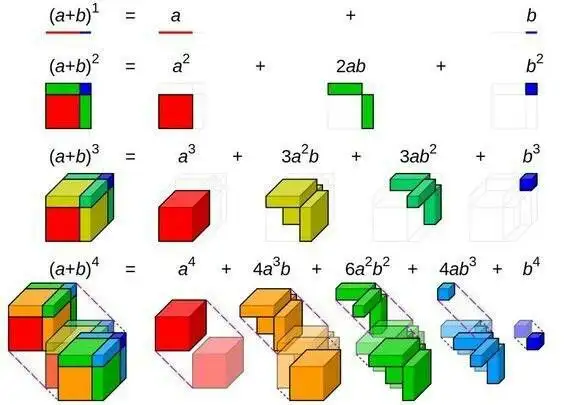
泰勒展开
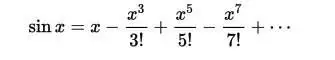
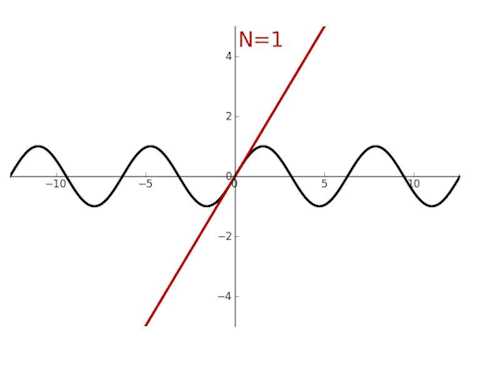
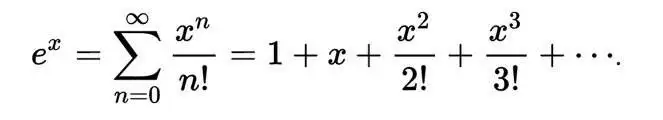
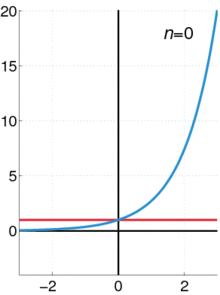
多边形外角和等于 360 度
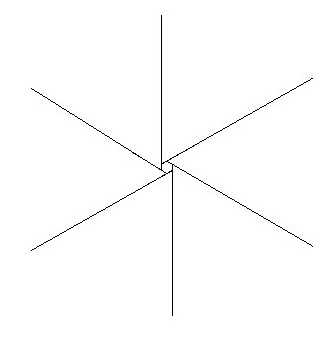
前 n n n 个数相加

不等式
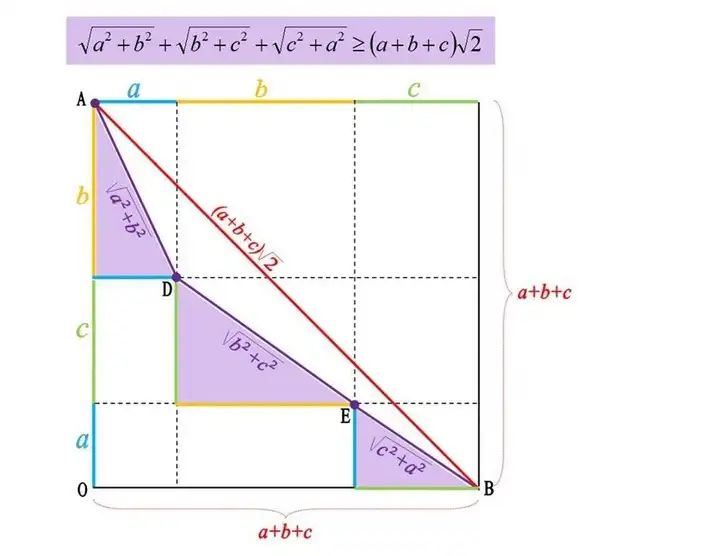
平方和与平方差

无穷级数求和
完全立方和公式
立方差公式
π \pi π 与理想弹性碰撞

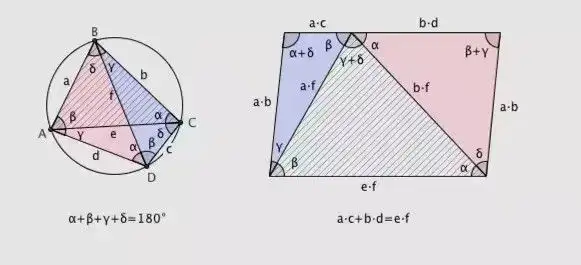
拖勒密定理
斐波那契数列
…
编辑于 2021-08-11 19:59_
via:
-
数学中有哪些漂亮的无字证明? - 知乎
https://www.zhihu.com/question/26899533 -
无穷等比级数和的无字证明
https://amathing.world/geometric-series-proof-without-words/ -
Proofs Without Words
https://www.geogebra.org/m/jFFERBdd

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








