字符串匹配之KMP---全力解析

近日，一同学面试被问到字符串匹配算法，结果由于他使用了暴力法，直接就跪了。字符串匹配方法大概有：BF(暴力破解法), 简化版的BM，KMP，BM，一般情况下，大家听说最多的应该就是KMP算法了。之前学习过，由于时间间隔比较大，记不太清楚了，今天上网查了下，发现写KMP的文章是不少，但是真正清晰简洁就没有了(july的文章太繁琐)，所以自己就研究了一晚上，弄清楚了kmp的计算过程，也就在此分享下。

1. 如果你现在完全不知道KMP是个神马玩意，请先阅读 阮一峰 的《字符串匹配的KMP算法》。

KMP算法最难理解的是就是next数组的计算过程，在此分享下我所理解的kmp算法以及next数组的计算过程(如果看前面理论比较头大，可以先看后面例子的计算过程，在回过头来看理论就会释怀)：

     1. next数组的计算过程: 

          申明:next数组下标从0算起, 定义next[0]=-1, next[1]=0; 模式串记为T[ ]

          假如求 T中 j+1 位的next[j+1]：

          将其 前一位(模式字符)的内容与其前一位的next值(next[j])的内容(T[next[j]])进行比较：

               如果它们相等(T[j]==T[next[j]])，则next[j+1] = next[j]+1;

               如果他们不相等，则继续向前寻找，直到找到next值对应的内容与前一位相等为止，则在这个next值上加一；

               如果直到第一位都没有与之相等，则next[j+1] = 0;           

           例: 有模式串 "abaababc"

          j=0时，next[0] = -1 ; j=1时，next[1] = 0;

          j=2时，t1!=t0, k=next[0]=-1, next[2]=0;

          j=3时，t2==t0, next[3] = next[2]+1 = 1;

          j=4时，k=next[3]=1, t3!=T[1], k=next[1]=0, T[3]==T[0], next[4]=next[1]+1 = 1;

          j=5时，k=next[4]=1, T[4]==T[1], next[5]=next[4]+1=2;

          j=6时，k=next[5]=2, T[5]==T[2], next[6]=next[5]+1=3;

          j=7时，k=next[6]=3, T[6]!=T[3], k=next[3]=1, T[6]==T[1], next[7]=next[3]+1 = 2;

      

     2. 上述算法的实现：

[cpp]  view plain copy

1. void calNext(const char *T, int *next){  
2.      int n = strlen(T);  
3.      next[0] = -1;  
4.      next[1] = 0;  
5.      int j=0, k=-1;  
6.      while(j<n){  
7.           if(k==-1 || T[j]==T[k]){  
8.                ++j;  
9.                ++k;  
10.                next[j] = k;  
11.           }  
12.           else  k = next[k];  
13.      }  
14. }  

     3. KMP主算法：

          设置比较起始下标: i=0, j=0;

          循环直到 i+m>=n 或者 T中所有字符都以比较完毕

               a. 如果 S[i]==T[j], 则继续比较S和T的下一个字符; 否则

               b. 将 j=next[j]， 从这位置开始继续进行比较;

               c. 如果j==-1, 则将 i 和 j 分别加1, 继续比较；

          如果T中所有字符均比较完毕，则返回匹配的起始下标，否则返回-1；

     4. KMP算法实现：

[cpp]  view plain copy

1. int kmpmatch(const char *S, const char *T){  
2.      if(S==NULL || T==NULL) return -1;  
3.      int n = strlen(S);  
4.      int m = strlen(T);  
5.      int next[m];  
6.      calNext(T, next);  
7.      int i=0, j=0;  
8.      while( i+m<n){  
9.           int k=i;  
10.           for( ; j<m&&i+m<n&&S[i]==T[j]; ++i, ++j) ;  
11.           if(j==m) return k;  
12.           j = next[j];  
13.           if(j==-1){  
14.                ++i;  
15.                ++j;  
16.           }  
17.      }  
18.      return -1;  
19. }  

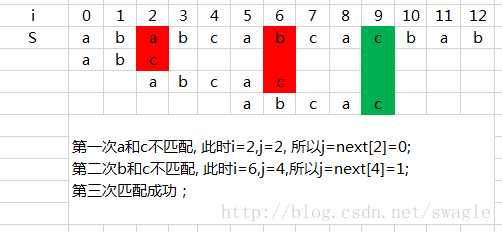
举例： 设主串 S="ababcabcacbab", 模式 T="abcac"

          按照上述方法计算得next[]={-1,0,0,0,1}