DRL实战 : N-Armed Bandits问题

最新推荐文章于 2022-11-27 13:15:51 发布

今晚打佬虎

最新推荐文章于 2022-11-27 13:15:51 发布

阅读量832

点赞数 1

分类专栏： DeepRL_in_action

本文链接：https://blog.csdn.net/u014281392/article/details/103988920

版权

DeepRL_in_action 专栏收录该内容

3 篇文章 0 订阅

订阅专栏

多臂强盗(n台老虎机)问题

在构建AlphaGo之前，先尝试一个简单的问题热热身， $n$ 台老虎机（多臂强盗问题),把对 $n$ 台老虎机操作看作是 $n$ 个不同的动作,即：每个动作 $a$ 对应一台特定的老虎机．在每次游戏 $k$ 中，玩家可以操作任意一台老虎机，这个操作即：动作 $a$ ,操作后玩家会获得奖励 $R (k)$ , 每台老虎机的奖励概率是固定的．

如何在这个游戏中获得更高的奖励

靠谱的策略是：

探索阶段：
- 尽可能的多玩几次，选择不同的机子，并观察每个机子（ $a$ ）对应的回报 $R_k(a)$ .
贪心阶段：
- 每次都之选择观察到平均回报最大的 $a$ .根据预期的回报来指导下一步的动作.
探索和贪心之间的权衡
- 停止探索：仅仅利用当前的信息，选择最佳的 $a$ ,可能会忽略全局最优的 $a$
- 随机探索：掌握更多的信息，避免陷入局部最优，但是要浪费更多的时间和金钱
- 贪心和探索之间的有效权衡才能最大化回报

值函数

用 $Q_k(a)$ 表示， $Q$ 函数是一个动作值函数，计算采取特定动作的价值．

$Q_k(a) = \frac{ \sum_{i=1}^k R_i}{k_a}$

$Q_k(a)$ : 第 $k$ 次游戏中对 $a$ 的预期奖励 = $a$ 获得奖励的算数平均值
$R_i$ : 动作 $a$ 之前获得奖励
$k_a$ : 动作 $a$ 被执行的次数

动作选择函数

$a = argmax_{a}([Q_k(a_1),Q_k(a_2), ...Q_k(a_n)　])$

动作选择函数的计算仅仅考虑我们探索过的动作，如果之前没有完全探索全部的动作，每次我们都只会在有限动作空间中做选择．为了避免陷入这样的局部最优，我们需要同时考虑探索和贪心的策略，在每一次游戏中，以一定的概率随机探索一个动作,剩下的概率中，根据值函数 $Q$ 和动作选择函数选择最佳的动作．其实就是，我们需要设置一个阈值 $\varepsilon$ ,每次游戏以 $\varepsilon$ 概率采取一些冒险的策略， $1-\varepsilon$ 采用贪心的策略．

# 遍历之前的动作找到reward的最高的动作
def get_best_action(actions):
    best_action = 0
    max_action_value = 0
    for i in range(len(actions)): 
        cur_action_value = get_action_value(actions[i]) 
        if cur_action_value > max_action_value:
            best_action = i
            max_action_value = cur_action_value
    return best_action

# 找到奖励最多的动作
def get_best_arm(record):
    arm_index = np.argmax(record[:,1],axis=0)
    return arm_index

probs initialization

初始化每个动作 $a$ 的奖励概率

n = 10                      # n 个机械臂
probs = np.random.rand(n)   # n 个机械臂概率的初始化

在这里插入图片描述

奖励函数

每个动作 $a$ 有一个奖励概率，每个动作的最高奖励为10美元。每次如果随机数小于 $a$ 的概率，它的奖励增加+1。完成10次迭代，返回最终的总奖励，奖励可能是0到10之间的任何值。如果某一动作的奖励概率为0.7，则执行尽可能多的该动作，平均奖励为7，但是在任何单次游戏中，为1~10之间的随机值。

def get_reward(prob, n=10):
    reward = 0;
    for i in range(n):
        if random.random() < prob:
            reward += 1
    return reward

每个动作执行2000次的奖励分布

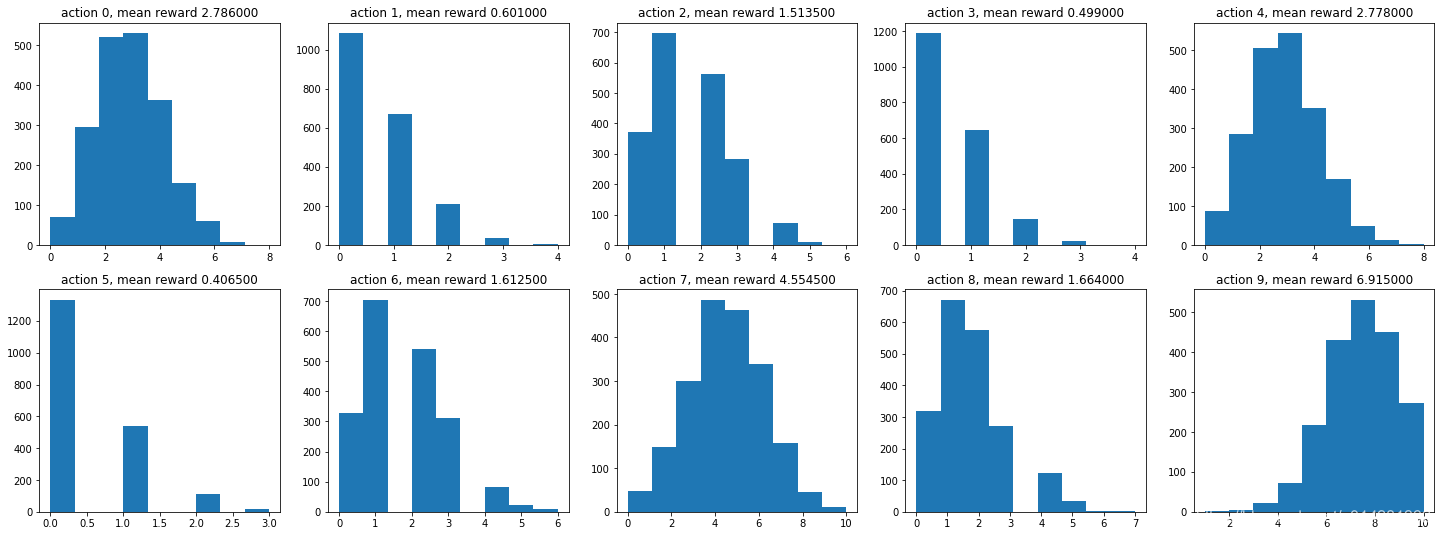
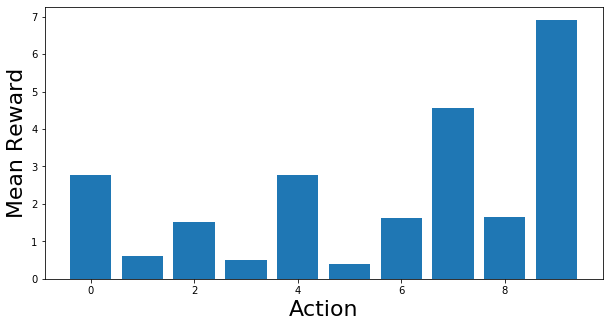
在这里插入图片描述

每个动作的平均奖励

在这里插入图片描述

初始化record

count : action 重复次数
avg reward : 平均奖励

# 10 actions x 2 columns
# Columns: Count #, Avg Reward
# 动作奖励二维表格

# 更新动作奖励二维数组
def update_record(record,action,r):
    new_r = (record[action,0] * record[action,1] + r) / (record[action,0] + 1)
    record[action,0] += 1
    record[action,1] = new_r
    return record

record = np.zeros((n,2))

print(record)

[[0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]]

600次模拟操作

$\varepsilon$ = 0.2, 随机值 > 0.2, 从record中找平均奖励最大的action
- 计算奖励，更新record
$\varepsilon$ 　< 0.2, 随机操作
- 计算奖励，更新record
$\varepsilon$ 值越大，随机探索的次数就越多，收敛的就越慢

def simulation_argmax(num_n, p=0.3):
    record = np.zeros((n, 2))
    rewards = [0]
    record_dict = {}
    actions = []
    for i in range(600):
        if random.random() > p:
            choice = get_best_arm(record)
        else:
            choice = np.random.randint(10)
        actions.append(choice)
        r = get_reward(probs[choice])
        record = update_record(record,choice,r)
        record_dict[i] = record.copy()
        mean_reward = ((i+1) * rewards[-1] + r)/(i+2)    # (r - reward[-1])/(i+1)+reward[-1]
        rewards.append(mean_reward)
    return rewards, record_dict, actions

Argmax : 累计平均奖励的变化

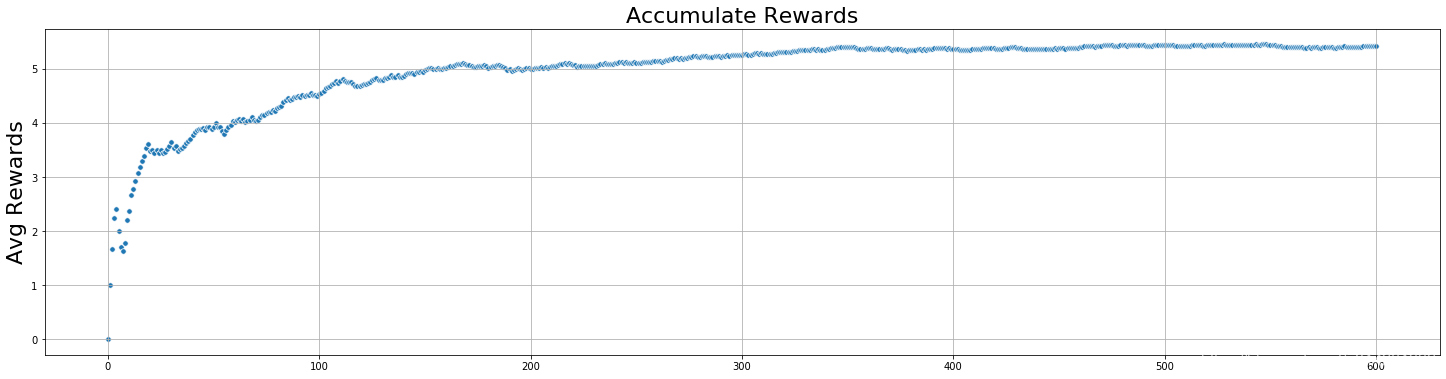
在这里插入图片描述

Argmax : 每个动作reward的变化

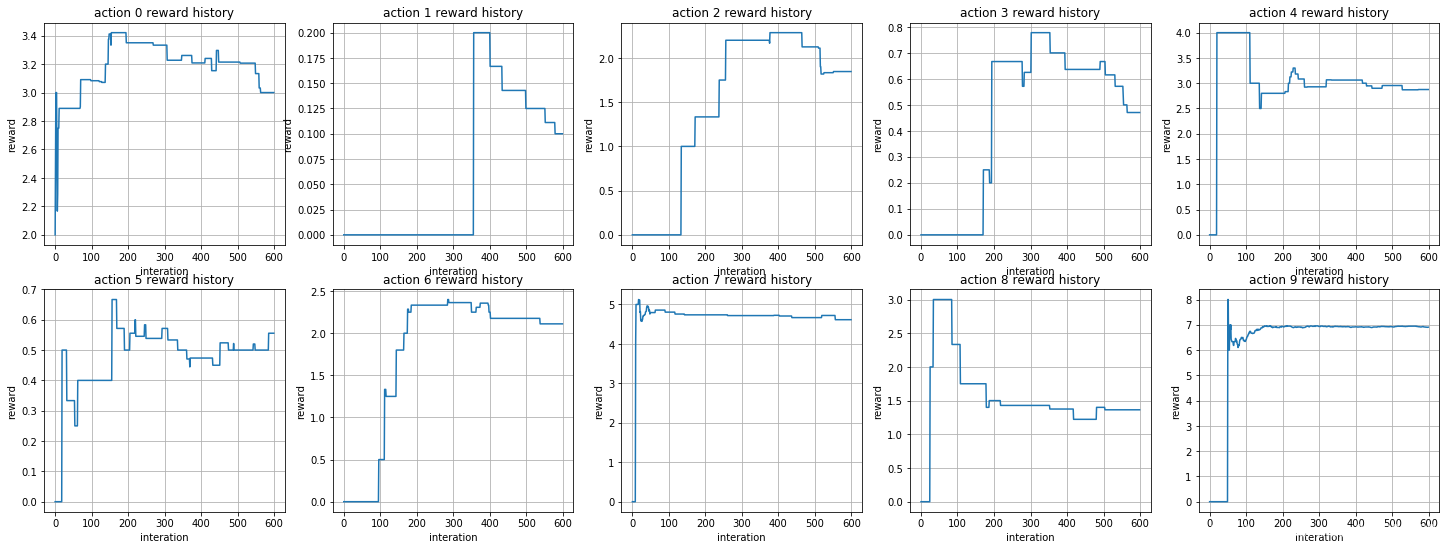
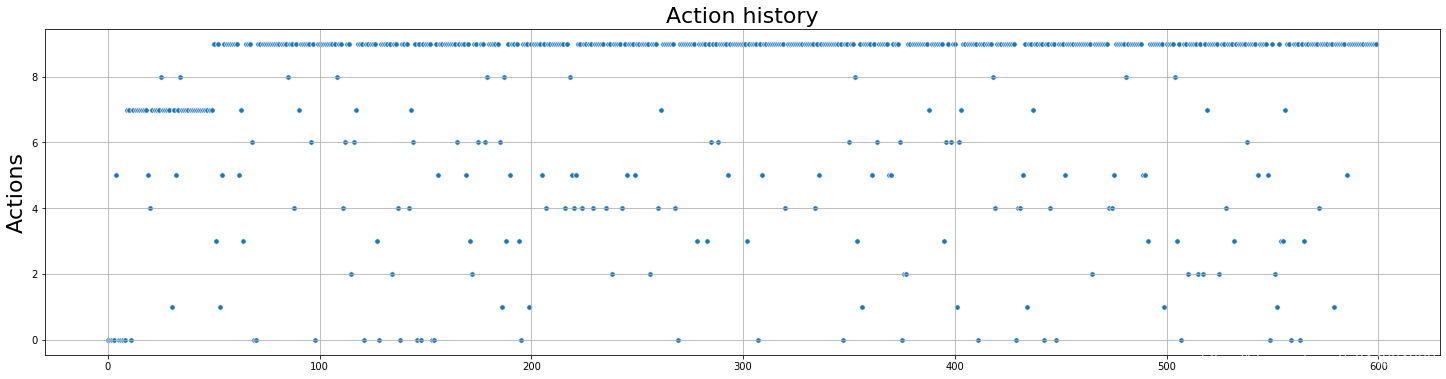
在这里插入图片描述

Argmax : 动作选择的变化

在这里插入图片描述

softmax选择策略

由上面的结果，我们可以发现，随着游戏的次数增加，累计的平均回报也在不断增加，每个动作的奖励也逐渐趋于稳定，从动作选择的变化来看，被选择次数最多的就是 $a_9$ ,从累计平均回报看，在游戏500次之后，已经趋于稳定了，但是动作选择策略仍会在进行随机选择，其实这个时候已经没有必要了，因为最优的动作已经被发现了，我们只用重复执行这一个动作就行了．我们需要一个新的动作选择策略，确保每次不选择最差的动作，但仍具有探索未知动作的能力。softmax刚好就满足这个需求，softmax不是在探索过程中随机选择一个动作，而是为我们提供了各种选择的概率分布。概率最大的选项等同于上面的最佳动作.

softmax方程:

$\frac{e^{Q_k(a)/ \tau}}{\sum_{i=1}^n e^{Q_k(a_i) / \tau}}$

$P r (a)$ : 接受动作的值，返回动作分布概率
$\tau$ : 调节参数，过大会是动作间的概率分布相似，过小会使动作之间的分布差异过大

def softmax(av, tau=1.11):
    softm = ( np.exp(av / tau) / np.sum( np.exp(av / tau) ) )
    return softm

 
p = softmax(record[:,1],t)     # 动作概率分布
choice = np.random.choice(np.arange(n),p=p)

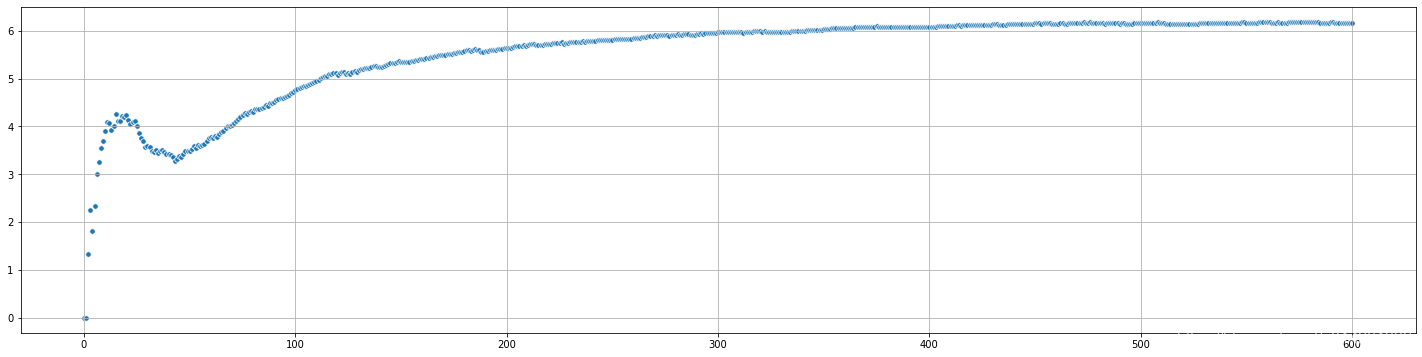
softmax()选择：累计回报的变化

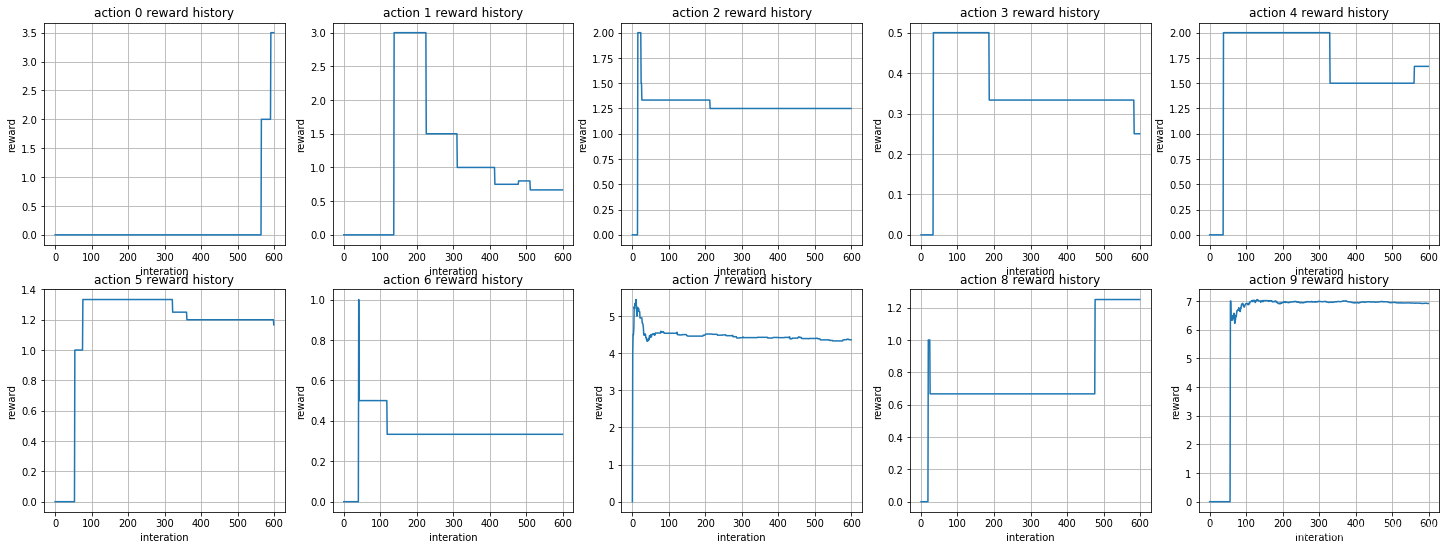
在这里插入图片描述

softmax : 每个动作的reward变化

在这里插入图片描述

Softmax : 动作选择的变化

在这里插入图片描述
从上面的结果来看，softmax()动作选择函数，收敛更快，对动作的选择更加集中．

Argmax : 不同 $P$ 值的影响

$\in [0, 1]$

Argmax : 不同 $P$ 值对rewards的影响

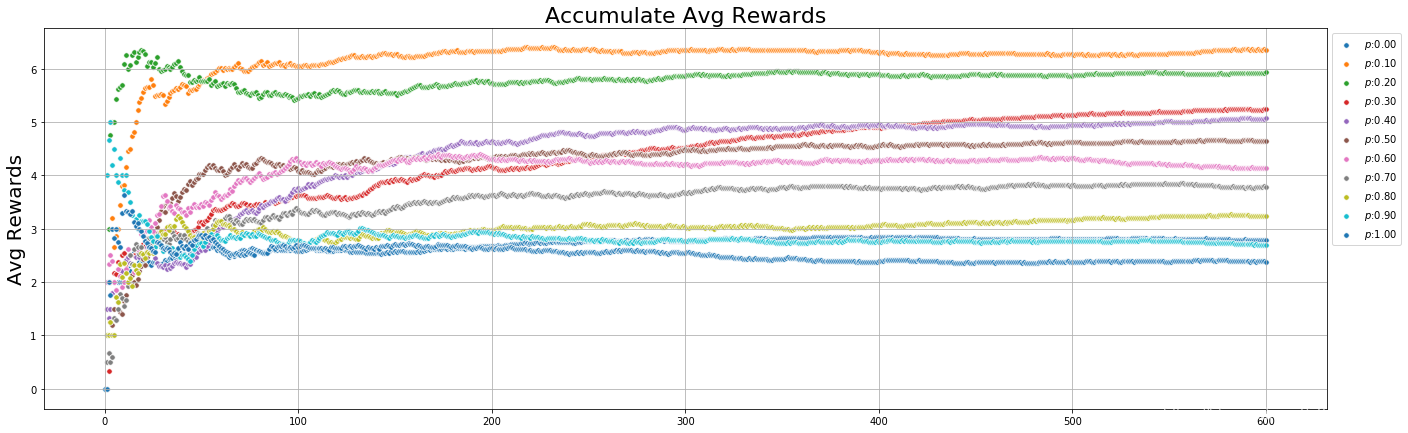
在这里插入图片描述

观察上图可知：

$P$ 在取值在两个极端的时候[0, 1]效果最差的
$P$ 然后从0.1~0.9递减

Argmax : 不同 $P$ 值对records的影响

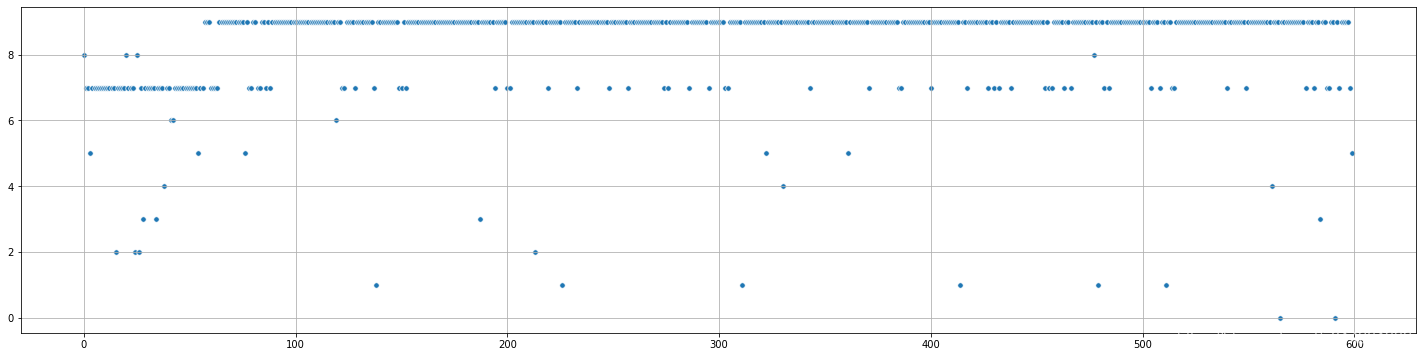
在这里插入图片描述

Argmax : 不同 $P$ 值对Actions的影响

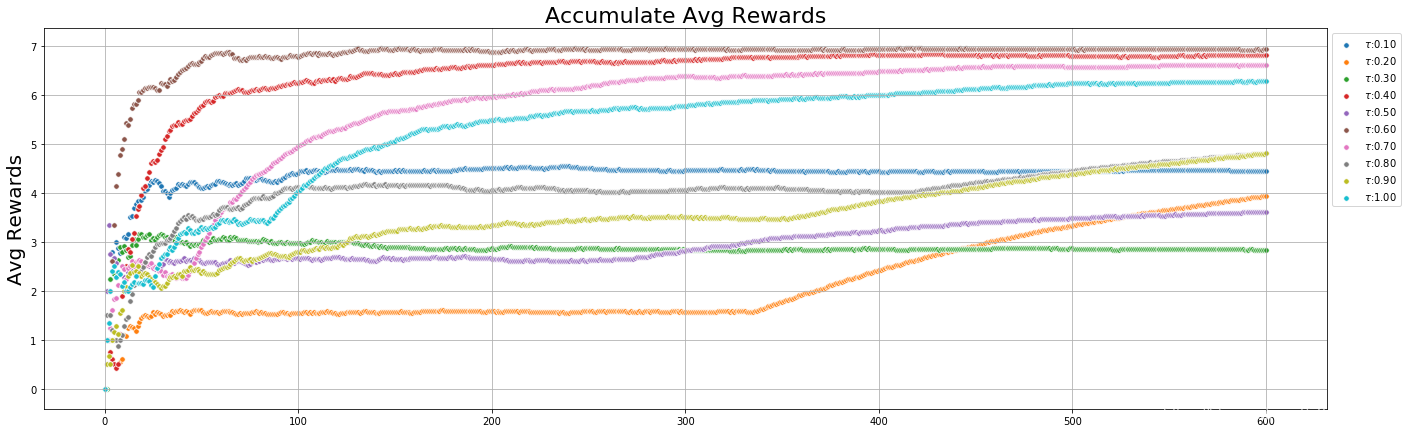
在这里插入图片描述

Softmax : 不同 $\tau$ 值的影响

$\tau \in [0.1, 1)$

Softmax : 不同 $\tau$ 值对rewards的影响

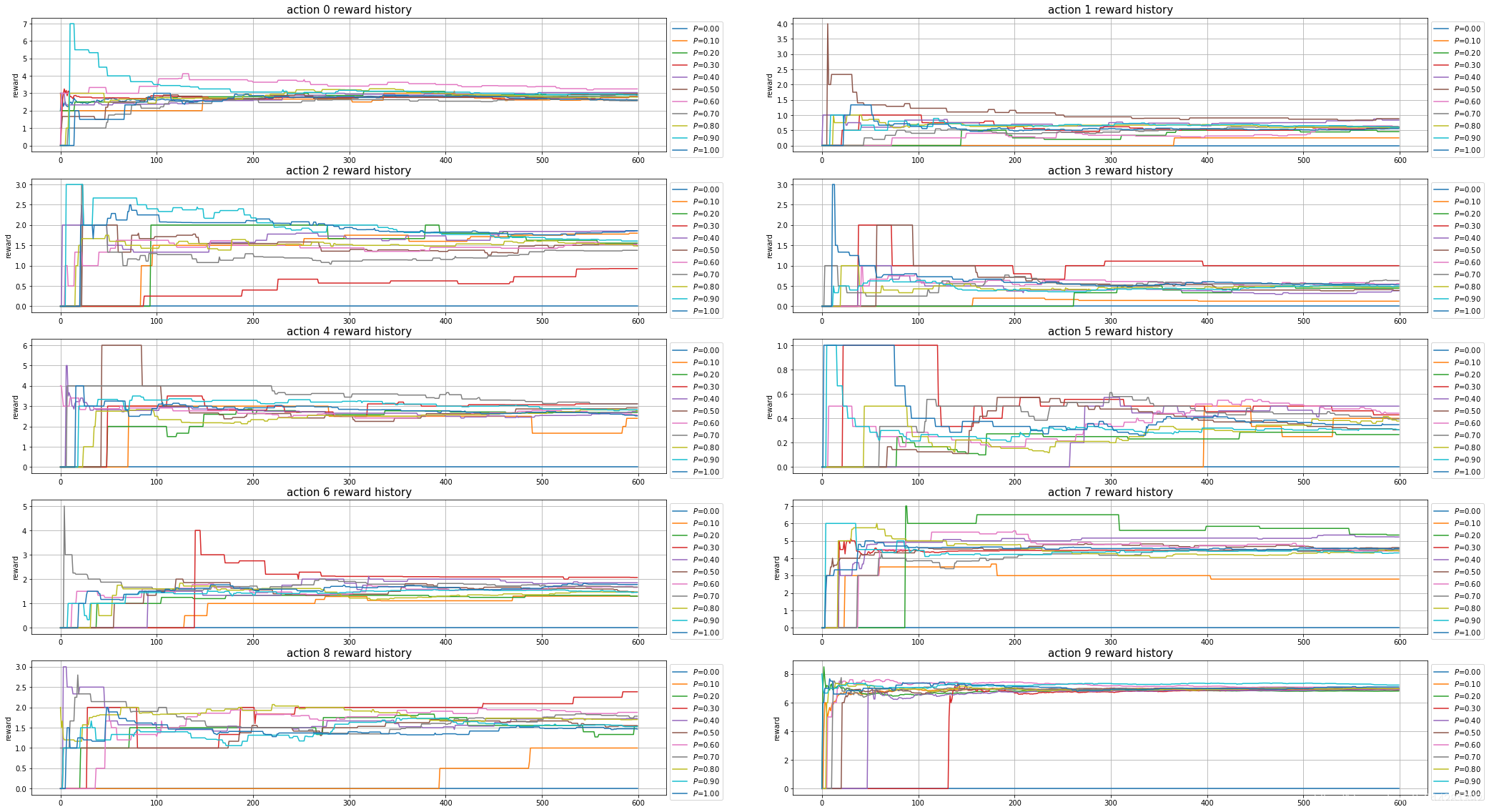
在这里插入图片描述

Softmax : 不同 $\tau$ 值对records的影响

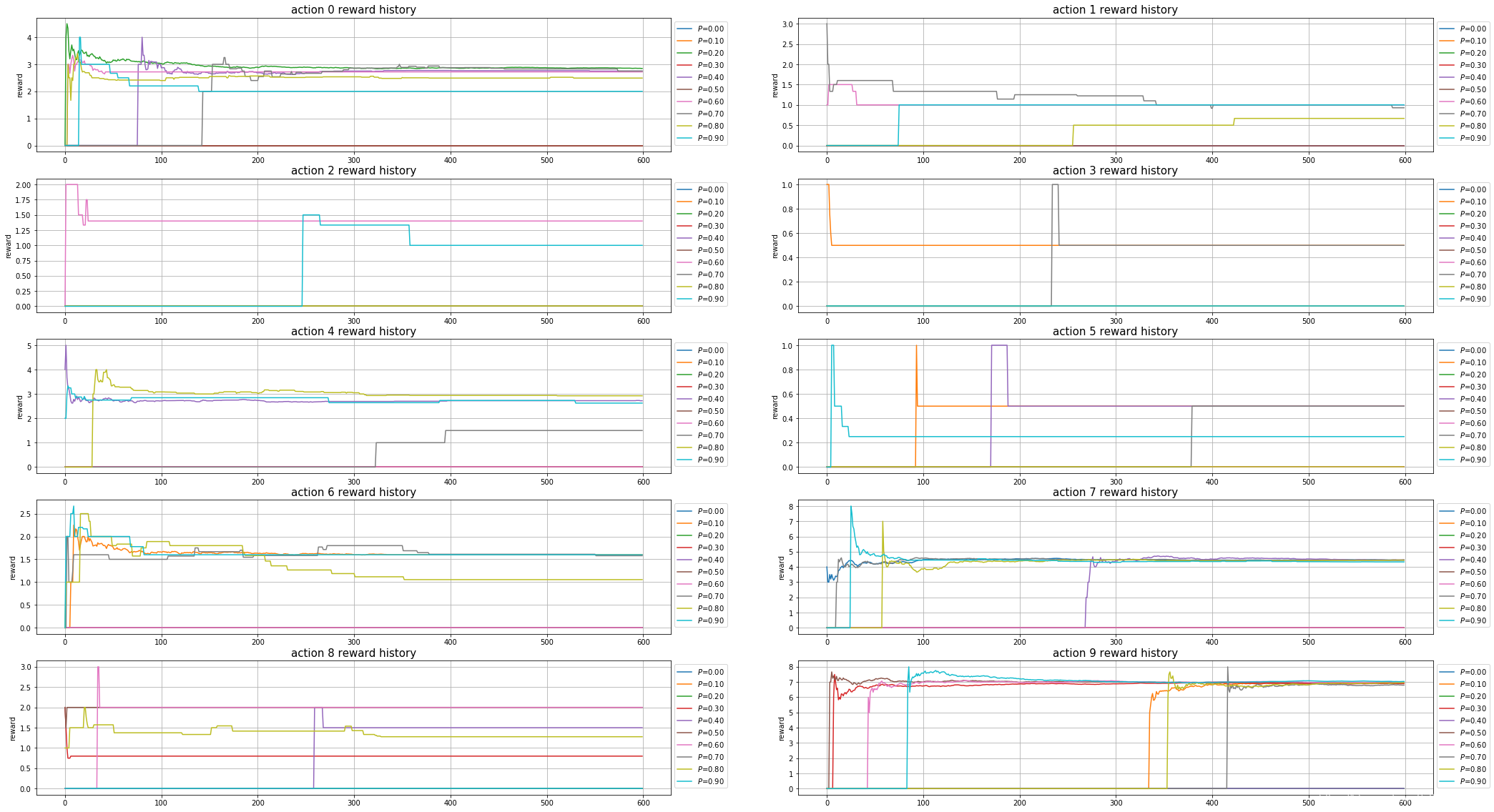
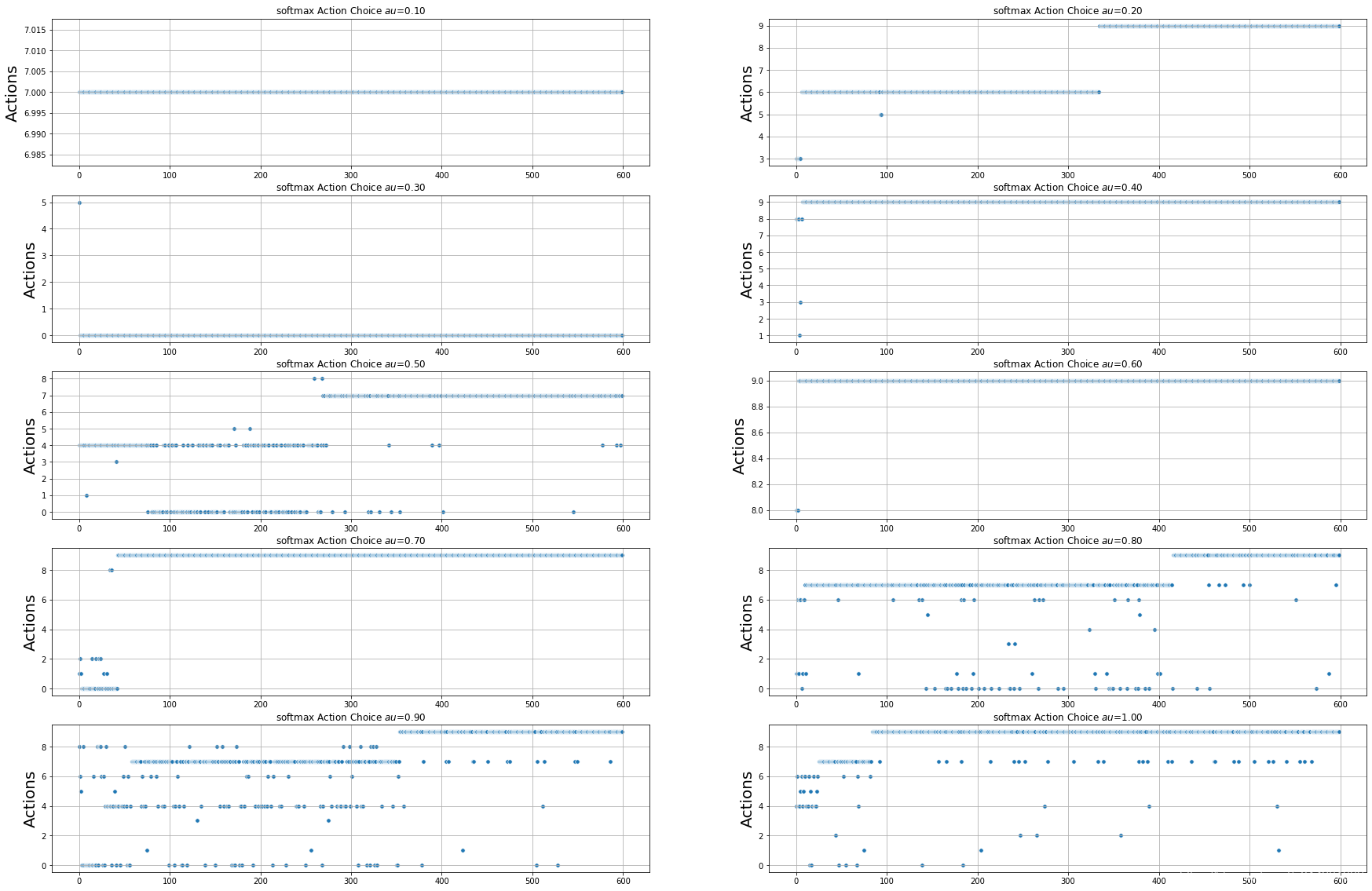
在这里插入图片描述

Softmax : 不同 $\tau$ 值对Actions的影响

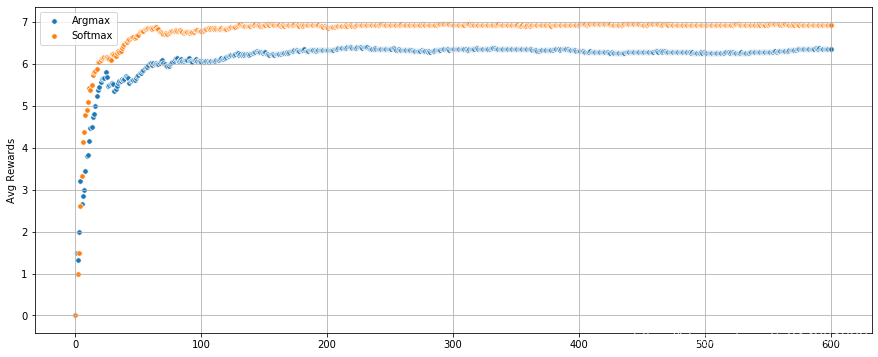
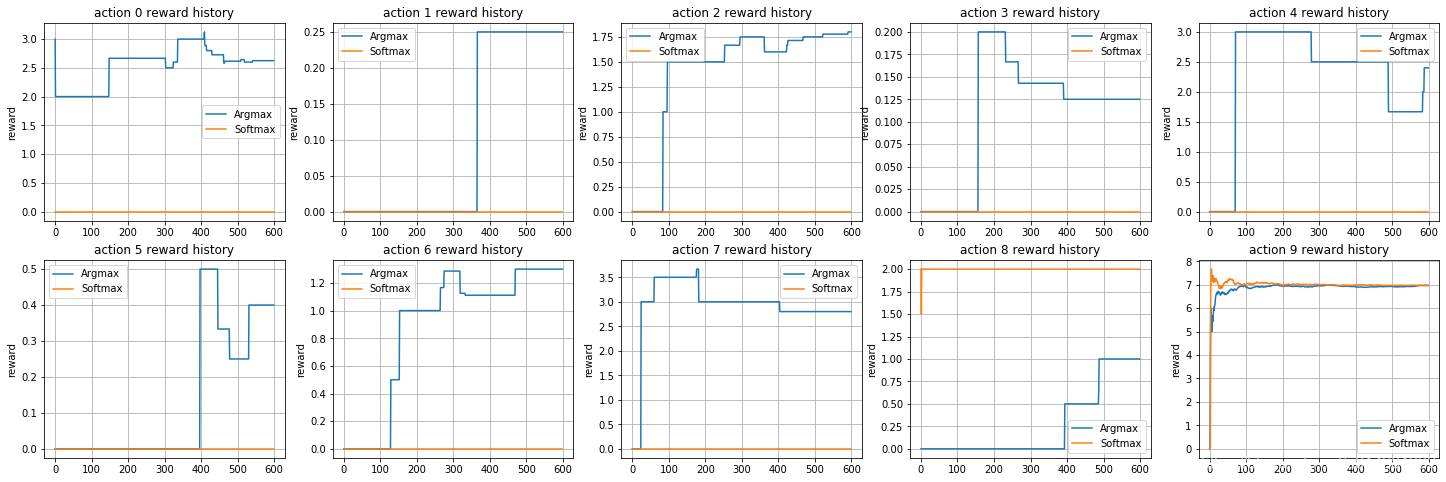
在这里插入图片描述

Final, Softmax Vs Argmax

Best Argmax : $P = 0.1$
Best Softmax : $\tau = 0.6$

Accumlate rewards

在这里插入图片描述

Records history

在这里插入图片描述

Actions

在这里插入图片描述

总结：

softmax可以更快的收敛，但是 $\tau$ 敏感，需要花时间找到最佳的 $\tau$ 值
argmax收敛的相对较慢，但是 $P$ 值的选择比较直观
- $P = 0 o r 1$ ,效果是最差的
- $p [0.1, 0.9]$ ,最终的累计回报是递减的
- 但是如果限制游戏的次数，适当的增加冒险的概率，可以更快的获得更高的奖励

今晚打佬虎

关注

1
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
DRL实战 : N-Armed Bandits问题

多臂强盗(n台老虎机)问题在构建AlphaGo之前，先尝试一个简单的问题热热身，nnn 台老虎机（多臂强盗问题),把对 nnn 台老虎机操作看作是 nnn 个不同的动作,即：每个动作 aaa 对应一台特定的老虎机．在每次游戏 kkk 中，玩家可以操作任意一台老虎机，这个操作即：动作 aaa,操作后玩家会获得奖励 R(k)R(k)R(k), 每台老虎机的奖励概率是固定的．如何在这个游戏中获得更高...
复制链接

扫一扫