基于LOUDS 的 Succinct Set 详解_louds succinct data structure-CSDN博客

前缀树

前缀树是一个高效的存储字符串集合的数据结构，通过同一个前缀共用节点来压缩信息，能够在随机的字符串集合中有着较好的压缩效率。举个例子，假设有一个字符串集合 [ab， abc， abcd， axy， buv] ，找这个集合构建的前缀树应该如下图所示。橙色的表示为叶子节点（定义为字符串结束）

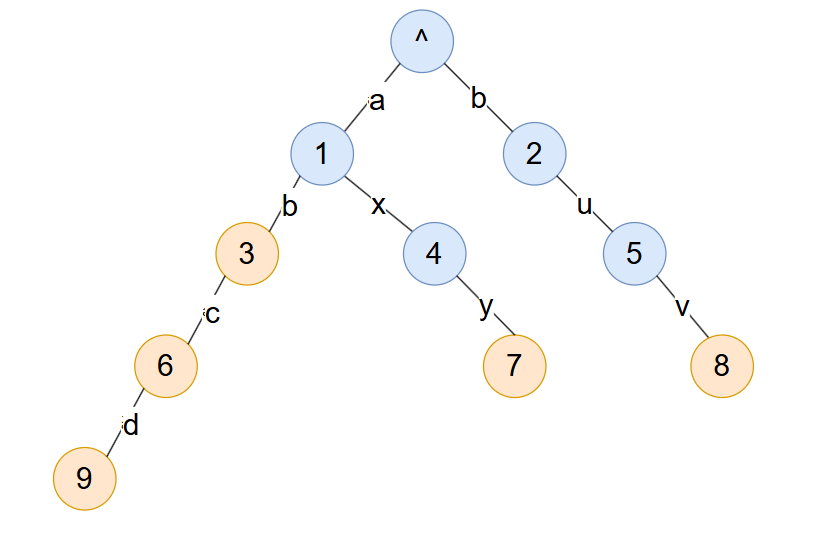
可以发现一样的前缀 ab 已经被合并为三个节点，可能在现在这里没有体现出来，但在非常大的数据集下压缩效率是非常显著的。

压缩前缀树

但是仍然不够，下面介绍基于Succinct Data Structure 构建的Succinct Set。

首先定义一个节点如何转化为一串字符，设节点有x个子节点，则该节点由x个0和1个1表示，最终如下图所示。

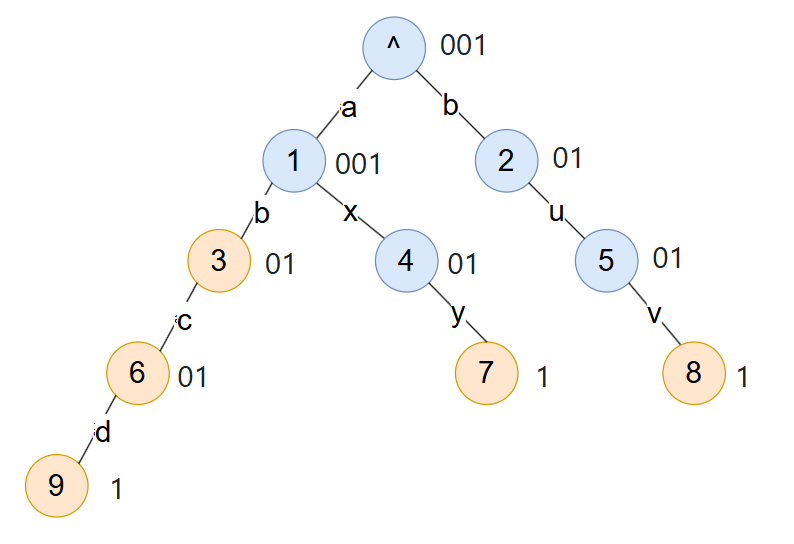
将整个前缀树按层序遍历拍平得到 001 001 01 01 01 01 01 1 1 1 。如下图所示

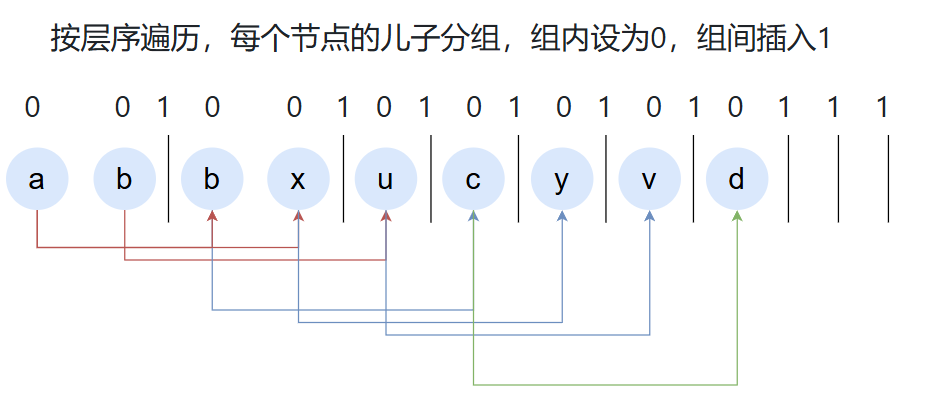
那怎么将其重新构建回一颗前缀树？

首先建一个表格，来看看数据和节点编号之间的关系？

	0	0	1	0	0	1	0	1	0	1	0	1	0	1	0	1	1	1	1
位置	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
编号	a	b	0	b	x	1	u	2	c	3	y	4	v	5	d	6	7	8	9

可以发现第 x 个节点的编号就是第 x 个1！那么定义第一个辅助函数 Rank1(r) 表示 [0, r] 中 1 的个数。那么第 i 个位置对应的编号就是 Rank(i) - 1 （必须为节点)

那我们知道一个节点编号如何定位回位置呢？可以发现就是1的位置！那么定义第二个辅助函数 Select(i) 表示第 i 个节点的位置！

于是我们得到了下面的新的表格

	0	0	1	0	0	1	0	1	0	1	0	1	0	1	0	1	1	1	1
位置	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
编号	a	b	0	b	x	1	u	2	c	3	y	4	v	5	d	6	7	8	9
Rank	0	0	1	1	1	2	2	3	3	4	4	5	5	6	6	7	8	9	10
Select	2	5	7	9	11	13	15	16	17	18

不知道缺少什么了，那么我们就来执行前缀树该有的功能来看看还差什么！

回到最开始的压缩前缀树的图。模拟搜索一下 axy

找到 a 的边，是位置 0 ，然后要跳到子节点 1

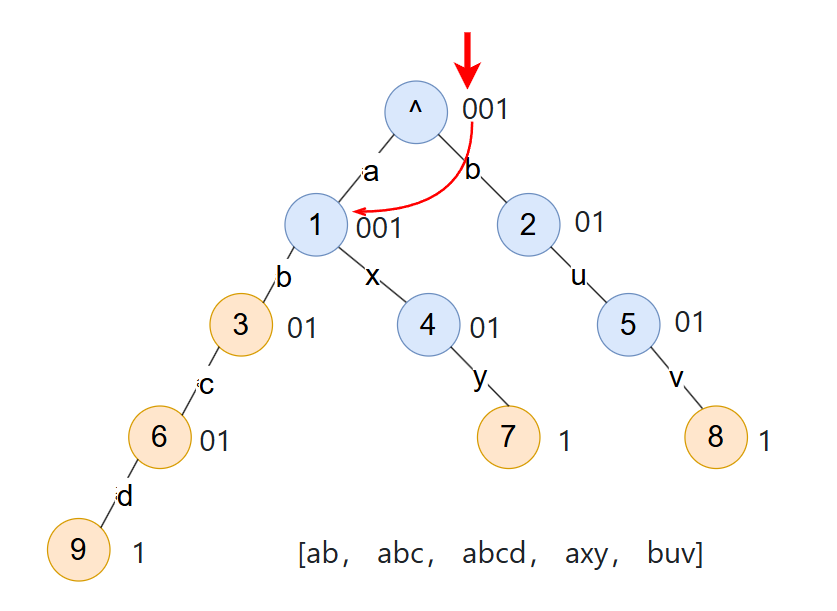
问题来了！我们怎么知道要跳到哪个节点？

考虑到是层序遍历得到的数据，每一个 0 其实都是对应着一个节点和一条边，又由于根节点没有边，则第 x 个 0 对应的就是第 x + 1 个节点！那就接着操作

找到 x 的边，是位置 3 ，然后要跳到子节点 4

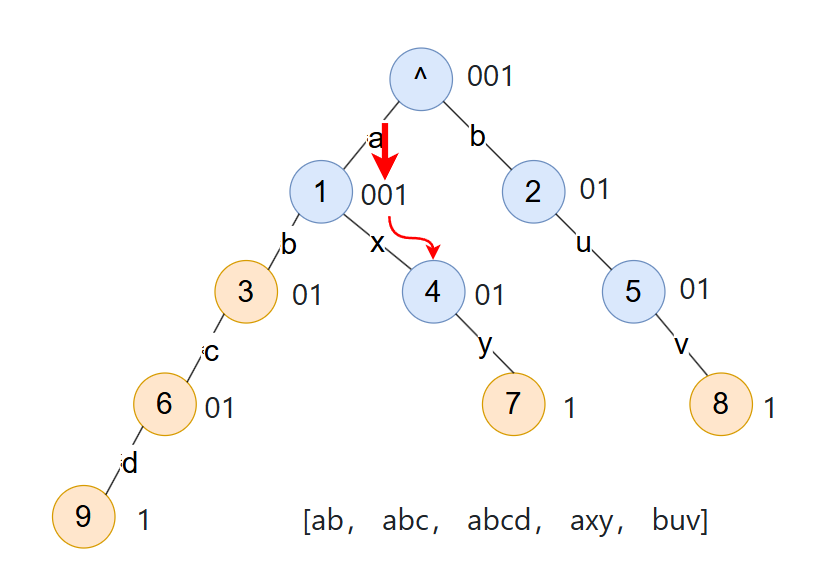
找到 y 的边，是位置 3 ，然后要跳到子节点 4

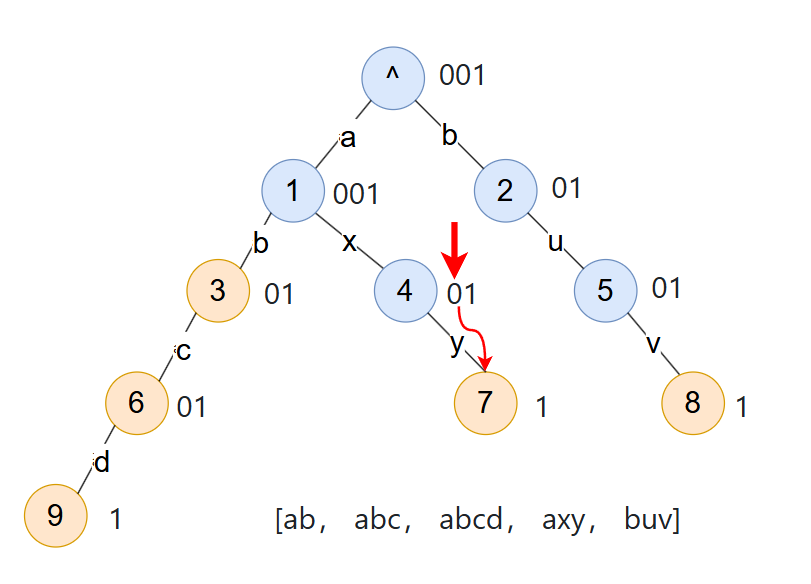
然后发现是叶子节点！这太巧了！发现压缩数据中并不能得知这个点是不是叶子节点，需要额外的标记，于是需要一个 leaves 数组来标记叶子节点，leaves[i] 为 1 表示节点 i 是叶子节点！

总结

辅助函数：Rank 和 Select

函数	作用	举个栗子 🌰
`Rank1(r)`	数一数前 `r` 个位置有几个 `1`	前5个位置有2个`1` → `Rank1(5)=2`
`Select(i)`	找第 `i` 个 `1` 藏在哪儿	第1个`1`在位置5 → `Select(1)=5`

为什么需要“终点标记”？

真相：压缩后的二进制串看不出哪里是单词结尾，就像一本书没了句号！
解决方案：用 leaves 数组当“小红旗” 🚩，标记哪些节点是终点。

对比：传统Trie Vs SuccinctSet Vs BinarySearch

200kweb2.txt（忽略构建时间），查询速度最慢可能是我写拉了

结构	内存占用(KB)	压缩率	查询速度(OPS)	适合场景
传统Trie	69367.78	2850%	1560000	动态的小型数据量
Succinct Set	1604.5	65%	740000	静态的海量字符串集合
BinarySearch	10836.37	445%	1680000	简单的使用场景

下面是简单的C++实现

#include <cstddef>
#include <cstdint>
#include <vector>
#include <string>
#include <queue>
#include <algorithm>

class BitMap {
    static constexpr size_t GAP = 64;
public:
    BitMap(size_t n = 0) : bits_((n + 63) / 64) {}
    void Set(size_t p, bool v = true) {
        if (bits_.size() <= (p / 64)) {
            bits_.resize(2 * (p / 64) + 1);
        }
        uint64_t mask = 1ULL << (p % 64);
        bits_[p / 64] = v ? (bits_[p / 64] | mask) : (bits_[p / 64] & ~mask);
    }
    bool Get(size_t p) {
        if (bits_.size() <= (p / 64)) {
            bits_.resize(2 * (p / 64) + 1);
        }
        return (bits_[p / 64] & (1ULL << (p % 64))) != 0;
    }
    size_t Size() const {
        return bits_.size() * 64;
    }
    size_t Rank(size_t r) {
        size_t block = r / 64, offset = r % 64;
        return ranks[block] + __builtin_popcountll(bits_[block] & ((1ULL << offset) - 1));
    }
    size_t Select(size_t k) {
        if (k == 0 || k > ranks.back()) return -1;

        // hit the precache;
        if (k % GAP == 0) {
            return selects[k / GAP - 1];
        }
        const size_t m = (k - 1) / GAP;
        size_t start_block = 0;
        if (m > 0) {
            start_block = selects[m - 1] / 64;
            k -= ranks[start_block];
        }

        for (size_t idx = start_block; idx < bits_.size(); ++idx) {
            uint64_t block = bits_[idx];
            size_t cnt = __builtin_popcountll(block);
            if (cnt < k) {
                k -= cnt;
                continue;
            }
            for (size_t i = 0; i < 64; ++i) {
                if (block & (1ULL << i)) {
                    if (--k == 0) return idx * 64 + i;
                }
            }
        }
        return -1;
    }
    
    void Precompute() {
        ranks.assign(1, 0);
        size_t cnt = 0;
        for (size_t i = 0; i < bits_.size(); ++i) {
            uint64_t block = bits_[i];
            ranks.push_back(ranks.back() + __builtin_popcountll(block));
            for (size_t j = 0; j < 64; j++) {
                if (block >> j & 1) {
                    cnt ++;
                    if (cnt % GAP == 0) {
                        selects.push_back(i * 64 + j);
                    }
                }
            }
        }
    }
private:
    std::vector<uint64_t> bits_;
    std::vector<size_t> ranks, selects;
};

class SuccinctSet {
public:
    explicit SuccinctSet(std::vector<std::string> keys) {
        std::sort(keys.begin(), keys.end());

        std::queue<std::tuple<size_t, size_t, size_t>> q;
        q.emplace(0, keys.size(), 0);
        size_t nodeCount = 0;
        for (size_t nodeId = 0; !q.empty(); nodeId ++) {
            auto [L, R, index] = q.front();
            q.pop();
            
            while (L < R) {

                while (L < R && keys[L].size() <= index) {
                    L++;
                    is_leaf_.Set(nodeId, true);
                }
                if (L == R) {
                    break;
                }

                int nL = L + 1;
                while (nL < R && index < keys[nL].size() && keys[nL][index] == keys[L][index]) {
                    nL++;
                }

                labels_.push_back(keys[L][index]);
                q.emplace(L, nL, index + 1);
                label_bitmap_.Set(nodeCount ++, false);
                L = nL;
            }
            label_bitmap_.Set(nodeCount ++, true);
        }
        label_bitmap_.Precompute();
    }

    bool Contains(const std::string &key) {
        size_t nodeId = 0, bitmapIndex = 0;
        for (char c : key) {
            while (bitmapIndex < label_bitmap_.Size()) {
                if (label_bitmap_.Get(bitmapIndex)) {
                    return false;
                }

                if (labels_[bitmapIndex - nodeId] == c) {
                    break;
                }

                bitmapIndex ++;
            }
            nodeId = bitmapIndex + 1 - label_bitmap_.Rank(bitmapIndex + 1);
            bitmapIndex = label_bitmap_.Select(nodeId) + 1;
        }
        return is_leaf_.Get(nodeId);
    }
private:
    std::vector<char> labels_;
    BitMap label_bitmap_;
    BitMap is_leaf_;
};