RSA加密原理

RSA加密原理

一、欧拉函数与欧拉定理

RSA加密算法和欧拉定理密切相关，欧拉定理又用到了欧拉函数，欧拉函数的定义如下：

对于正整数n，欧拉函数是小于等于n的正整数中与 n 互质的数的个数。

互质指两个整数的最大公约数为1，例如互质的有：

3、5

2、9

13、14

不互质的例如有：

2、4

256、32

999、666

明显的，1与任何数互质，所以大于等于1。

对于8来说，与它互质的有1、3、5、7，所以。

对于7来说，与它互质的有1、2、3、4、5、6，所以。

对于13来说，与它互质的有1到12，所以φ(13) = 12，不难得出n为质数的时候，。

理解了欧拉函数，咋们再来看欧拉定理：

对于互质的正整数p、q，则p的φ(q)次方与1同余，模为q。

即，因为1模q必为1，也等同于。如果对同余迷糊的话，的意思就是a除以c的余数和b除以c的余数相等。

二、大质数乘积

RSA算法的可靠性在于大数分解质因数的困难，比如p、q均为很大的质数，仅仅知道p*q的结果，想求解p、q则特别困难。理论上的量子计算机上的Shor算法就是分解质因数的算法，如果得以实现，现有的加密体系就会失效。例如银行、核武器等各种机密都需要重新寻找可靠的加密方式。

RSA算法首先寻找两个大质数p与q，然后得出。欧拉函数是积性函数，满足的性质，所以。又因为n为质数的时候，，而p、q均为质数，所以。

三、模反元素

对于互质的正整数p、q，一定可以找到一个数d满足，d就叫做p对模数q的模反元素。

为何d一定存在？因为欧拉定理，，d至少存在为。

四、公钥的计算

假设公钥为对，用于加密信息。私钥为对，用于解密信息。公钥是所有人都知道的信息，如果有人需要给我发送信息，就需要用这个公钥处理后再发送，即使第三者知道了处理后的信息和公钥也无法还原到加密前的信息。

先来看公钥是如何生成的，n为两个质数p、q的乘积。e与互质，且小于。所以首先生成两个大质数p与q，然后计算出n。因为p、q是质数，通过不难计算出的值，由于质数与其他数都互质，所以e最小可以是3，也有文章说实际应用一般选65537。

五、私钥的计算

私钥的d为，e对模数的模反元素，即满足，其中e和互质（上一节所求出的e值）。通俗的说就是e*d除以余数等于1，即 。

欧几里得算法简称gcd，也叫做辗转相除法，用于计算两个正整数的最大公约数。基本公式为，所以可以编写如下程序：

template <typename T>
T gcd(T a, T b)
{
    return b ? gcd(b, a % b) : a;
}

而公钥d的计算需要用到扩展欧几里得算法，原理基于：

对于两个整数的最大公约数，必然存在整数x和y满足。

所以可以编写如下代码：

template <typename T>
T exgcd(T a, T b, T& x, T& y)
{
    if(!b)
    {
        x = 1;
        y = 0;
        return a;
    }
    T r = exgcd(b, a%b, x, y);
    T t=x;
    x = y;
    y = t - a / b * y;
    return r;
}

所以等式可表示为 ，，求出x的值即为d。

六、加密解密与安全性

设密文为C，明文为M，使。则，。

发送方使用公钥使明文M变为密文C后，密文通过公有渠道发送给接收方，在过程中即使其他人知道公钥并窃取到了密文，也是无法知道明文的。因为明文只能通过第二个公式中的密钥的d计算得到，由于d不需要在网络上传输，也就不太可能被别人知道。由于知道n，可以通过分解n得到p、q来破解。不过大数质因数分解需要特别长的时间，所以不太现实。也可以直接计算出或者直接试出来d的值，不过一个围棋的走法就比宇宙的原子数还多，对于幂次的数量增长是很夸张的。因为这个质数相乘的步骤很简单，不过反过来就很难得出了，这就是非对称加密的特点。假设利用M = C + 3，或者M = C ^ 2之类的算法加密解密，一旦破解者知道了算法原理，就不难得出 C = M - 3，C = sqrt(M) 的解密方法。而 这样的式子就没办法写成这种能快速计算的式子，必须利用密钥的d才能快速的计算出明文。

七、解密公式的证明

C是由加密公式得到的，不过怎么得出 的呢？数学家们往往会通过直觉假设，然后再逻辑性的证明。如果假设与事实相当符合，就已经成功了，不过能够逻辑上的证明才会用得心里踏实。

一个数求模的余数必然和它同余，所以，同余具有乘方性质，又因为所以。由于M小于n，所以只要 即可证明，即等同于证明。

当M与n互质时，代入欧拉定理得，乘方性质得，乘法性质得，所以M与n互质时得证。

当M与n不互质时，因为n分解因式只能等于p*q，所以M必须有p因子或者q因子，即M=hp，或M=hq。假设M=hq，又因为M小于n，所以p、q不能都是因子，所以M与p互质。代入欧拉定理得，乘方性质得，好吧，根据和乘法性质得出。所以，由于其中余数被抵消了，所以相减会是j倍的p。所以，因为这个式子的左边是q的整数倍，所以右边也必须是q的整数倍，所以jp是q的整数倍，因为p与q互质，所以j必须是q的整数倍，所以令j = tq可得，即，所以，这样就证明了，同理M=hp的时候也一样。

综上所述就证明了，至于利用到的欧拉定理、欧拉公式、同余的计算性质、欧几里得算法等等，我就不再证明了，请站在巨人的肩膀上！

八、计算需求

首先我们需要表示一个较大的数字，编程语言自带的类型最大一般只有64位远远不够。而RSA的要求是1024至更多，所以需要大数类，并且实现相关的计算，C#与JAVA都有BigInteger类，可惜是C++标准库没有。

其次我们需要寻找大素数，在n位置处随机选取个数字来检验它是不是质数。素性检验先使用费马检验，然后再使用Miller-Rabin测试，不过仍有极低的概率出错。

素数分布函数的意思是小于等于x的素数个数，之所以在n处挑选个，是由于素数定理说明了随机选取一个整数n是质数的概率为。素数定理：

至于公钥的e一般直接使用65537，然后使用扩展欧几里得算法计算出私钥d。加密和解密就需要的是幂模计算。由于只有幂模运算在加密解密中使用，所以它的速度最重要。不过《算法导论》已经给出了有效的方法求 的值了。叫反复平方法，至于它的原理大概是，我初步改写后的代码如下：

template <typename T>
T modular_exponentiation(T a, T b, T n)
{
	T d = 1;
	T k = sizeof(T) * 8 - 1;
	for (T i = k; i >= 0; --i)
	{
		d = (d * d) % n;
		if ((b & (1 << i)))
		{
			d = (d * a) % n;
		}
	}
	return d;
}

用int型初步测试了下，在值比较小的时候没有问题，稍微大一点就会有问题。

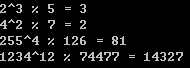
至于如何将这些算法应用到大数上，就需要更多特定的算法了。由于太过繁琐，一两天是肯定研究不透了，看来实践的难度并不比理论低（学习理论，而不是发明理论，发明理论的难度更不可及了），所以我决定就此打住了，Java和C#都有大数类，不过C++标准库没有，所以我也不想再进一步造轮子了，知道原理即可。