「信号」信号分析与处理（二）

傅立叶级数 Fourier Series

---

傅立叶的发现

十八世纪中到十九世纪初，随着热力学的蓬勃发展，求解热传导方程变成了一个焦点问题。而傅立叶级数便是傅立叶在1805年左右研究热传导方程的解的时候提出的一种巧妙解法。

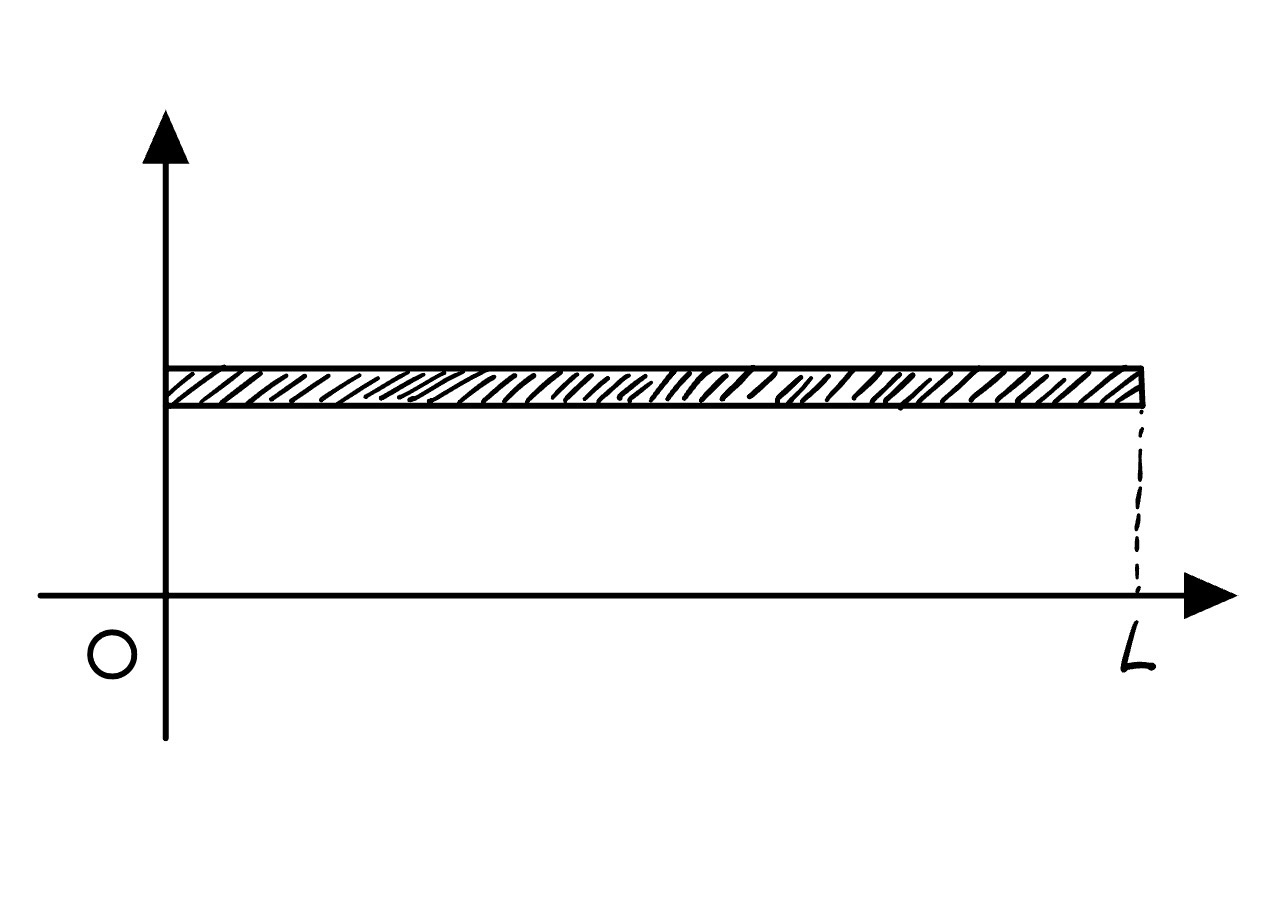
先来介绍一下一维的热传导方程

如图是一根均匀导热的杆子，若我们知道这跟杆子上每一点的温度，标识为$f(x,t)$，要解决的问题是

已知$f(x)=f(x,0)$

求$f(x,t),当t>0$

有前人根据热力学的基本理论推出了热力学方程的形式，即

$\frac{\partial f}{\partial t}=k\frac{{\partial }^{2}f}{\partial x^2}$

$f(x)=f(x,0)$

显然，直接入手解出一个通解是非常难得，更何况这只是一维的情况，三维以上的方程更是难解。对此，傅立叶提出了一个特殊解。而这个特殊解没有那么“特殊”，他足够代表一大部分的函数。

$当f(x)=B时,有f(x,t)=B$，/理解：如果杆子上每个点温度都一样，而杆子本身不对外辐射热量，那么任何时候杆子上各个点温度都一样且不变

$当f(x)=Bcos({\omega }_{0}x)时,有f(x,t)=Bcos({\omega }_{0}x)e^{-k{\omega }^{2}t}$

$当f(x)=Csin({\omega }_{0}x)时,有f(x,t)=Csin({\omega }_{0}x)e^{-k{\omega }^{2}t}$

如果$f(x)=B_0+{\Sigma }_1^{\infty }{B}_{k}cos(k{\omega }_{0}x)+{\Sigma }_1^{\infty }{C}_{k}sin(k{\omega }_{0}x)$

那么热传导方程的解就是

$f(x,t)=B_0+{\Sigma }_1^{\infty }{B}_{k}cos(k{\omega }_{0}x)e^{-K{k}^2{\omega }^{2}t}+{\Sigma }_1^{\infty }{C}_{k}sin(k{\omega }_{0}x)e^{-K{k}^2{\omega }^{2}t}$

这种三个特殊解的组合，说明热传导方程是一个LTI系统，输入和输出满足叠加性。

必须指出，傅立叶埋了一个坑：

这些${\omega }_0$都不是随便取的，而叫做基波频率，$k{\omega }_0$叫做k次谐波频率，$B_0$叫做直流分量

---

连续时间的傅立叶级数

现在这个理论还不够完备。该如何让我们能够通过$f(x)$的表达式，求出$B_0,B_k,C_k$呢？一旦我们求出这几个量，就一定可以把$f(x)$写成傅立叶级数形式，就一定可以把$f(x,t)$写出来。读完这一推导我们将知道，傅立叶之所以要假定${\omega }_0$不是随便取的，就是为了方便求出$B_0,B_k,C_k$

通过等式$f(x)=B_0+{\Sigma }_1^{\infty }{B}_{k}cos(k{\omega }_{0}x)+{\Sigma }_1^{\infty }{C}_{k}sin(k{\omega }_{0}x)$两边同时取一个周期内的积分，可以消除正余弦项，通过两边同时乘以cos/sin，取一个周期的积分，可以消除常数项和正余弦的其中一项。

$B_0=\frac{1}{T_0}{\int }_{T_0}f(x)dx$

$B_k=\frac{2}{T_0}{\int }_{T_0}f(x)cos(k{\omega }_{0}x)dx$

$C_k=\frac{2}{T_0}{\int }_{T_0}f(x)sin(k{\omega }_{0}x)dx$

什么样的函数能表示为这样的形式呢？傅立叶没有给出回答，但狄里赫利给出了条件

$f(x)$在一个周期内绝对可积

$f(x)$在一个周期内最值有限

$f(x)$在一个周期内断点有限

我们不禁要发问，想必当时的人们也要发问：自然界的呈现的函数，难道真的都是这样子由常数项和正弦级数项构成的吗？恐怕这不是现在能够被解答的问题了。

傅立叶级数：更常用的表达形式->复指数形式

$x(t)={\Sigma }_{-\infty }^{+\infty }{a}_k{e}^{jk{\omega }_{0}t}$

$a_k=\frac{1}{T_0}{\int }_{T_0}x(t)e^{-jk{\omega }_{0}t}dt$

通过欧拉公式，复指数形式的傅立叶级数是可以和正弦形式的傅立叶级数互化的。

---

连续时间傅立叶级数性质

线性性质

$x(t)\stackrel{Fs}{\leftrightarrow }{a}_k$

$y(t)\stackrel{Fs}{\leftrightarrow }{b}_k$

$z(t)=Ax(t)+By(t)\stackrel{Fs}{\leftrightarrow }{c}_k=A{a}_k+B{b}_k$

时移性质

$x(t-t_0)\stackrel{Fs}{\leftrightarrow }{a}_k{e}^{-jk{\omega }_0{t}_0}$

时间反转性质

$x(-t)\stackrel{Fs}{\leftrightarrow }{a}_{-k}$

时域尺度变换性质

$x(\alpha t)\stackrel{Fs}{\leftrightarrow }{a}_k$

虽然傅立叶系数本身没改变，但是它对应的级数改变了

相乘性质

$x(t)\stackrel{Fs}{\leftrightarrow }{a}_k$

$y(t)\stackrel{Fs}{\leftrightarrow }{b}_k$

$x(t)y(t)\stackrel{Fs}{\leftrightarrow }{h}_k={\Sigma }_{l=-\infty }^{+\infty }{a}_l{b}_{k-l}$

共轭性质

$x(t)\stackrel{Fs}{\leftrightarrow }{a}_k$

$x^{\ast }(t)\stackrel{Fs}{\leftrightarrow }{a}_{-k}^{\ast }$

当$x(t)$为实数函数，$x(t)=x^{\ast }(t)$，所以$a_k=a_{-k}^{\ast }$，也即$a_{-k}=a_k^{\ast }$

进一步，$x(t)$为实偶函数，$x(t)=x(-t)=x^{\ast }(t)=x^{\ast }(-t)$，那么$a_k=a_{-k}=a_k^{\ast }$。所以**$a_k=a_k^{\ast }$**。

相应地，$x(t)$为实奇函数，$x(t)=-x(-t)=x^{\ast }(t)=-x^{\ast }(-t)$，那么$a_k=-a_{-k}=-a_k^{\ast }$。所以**$a_k=-a_k^{\ast }$**。

P.f.

$x(t)={\Sigma }_{-\infty }^{+\infty }{a}_k{e}^{jk{\omega }_{0}t}$

$x^{\ast }(t)={\Sigma }_{-\infty }^{+\infty }{a}_k^{\ast }{e}^{-jk{\omega }_{0}t}$，两边取共轭

令k=-k，$x^{\ast }(t)={\Sigma }_{-\infty }^{+\infty }{a}_{-k}^{\ast }{e}^{jk{\omega }_{0}t}$

这样就可以看出对应关系：$x^{\ast }(t)\stackrel{Fs}{\leftrightarrow }{a}_{-k}^{\ast }$,

---

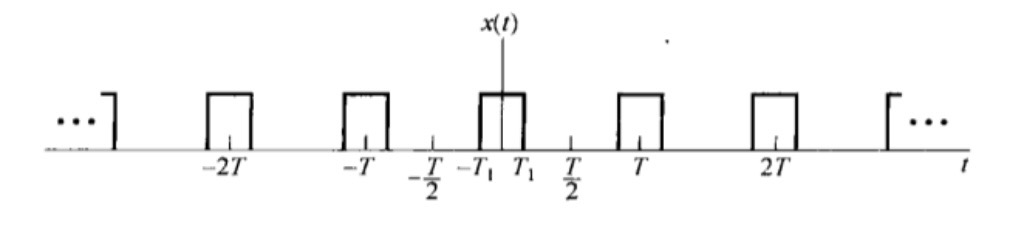
e.g 求周期方波信号的傅立叶级数

可以使用傅立叶的三角正弦级数形式来进行计算。观察这个函数可知为偶函数，所以${\Sigma }_1^{\infty }{C}_{k}sin(k{\omega }_{0}x)=0$。而$B_0=\frac{1}{T}{\int }_{-T/2}^{T/2}x(t)dt=\frac{2T_1}{T}$

$B_k=\frac{2}{T}{\int }_{-T/2}^{T/2}x(t)cos(k{\omega }_{0}t)dt=\frac{2}{k\pi }sin(\frac{2k\pi T_1}{T})$

而再用一次傅立叶的复指数级数形式来计算：

$$\begin{gathered} a_k=\frac{1}{T}{\int }_{T}x(t)e^{-jk{\omega }_{0}t}dt \\ =\frac{1}{T}{\int }_{2T_1}{e}^{-jk{\omega }_{0}t}dt \\ =\frac{1}{jk{\omega }_{0}T}2jsin(k{\omega }_0{T}_1) \\ =\frac{2sin(k{\omega }_0{T}_1)}{k{\omega }_{0}T} \\ =\frac{sin(\frac{2k\pi }{T}{T}_1)}{k\pi } \end{gathered}$$

$\therefore x(t)={\Sigma }_{k=-\infty }^{+\infty }\frac{sin(\frac{2k\pi }{T}{T}_1)}{k\pi }{e}^{jk{w}_{0}t)}$

可以发现，$k=0,a_k=\frac{2T_1}{T}$，和上面的$B_0$对应

如果$T=8T_1$，那么：

---

离散时间的傅立叶级数

一个很关键的问题是，连续时间的复指数是非周期的，而离散时间的复指数是周期的，也就是说：$e^{j{\omega }_{0}n}=e^{j{\omega }_0(n+N)}$。

也就是说，离散情况下，复指数信号集中只有N个信号是不相同的。而连续情况下，每个复指数信号都是互不相同的。这也就是离散和连续的傅立叶级数唯一不同的点了。基于这个，可以容易的推出离散时间的傅立叶级数对：

$x[n]={\Sigma }_N{a}_k{e}^{jk{\omega }_{0}t}$

$a_k=\frac{1}{N}{\Sigma }_{N}x[n]e^{-jk{\omega }_{0}n}$

---

傅立叶级数在LTI系统中如何生效

傅立叶级数可以表示大部分的连续时间的信号和离散时间信号，而我们又已经知道了系统是怎么处理信号的（卷积）。接下来，将“表示信号”和“处理信号”结合起来。

前面提到，之所以要选复指数，就是因为它是系统的特征函数。

连续时间下$e^{st}\to H(s)e^{st}$

离散时间下$z^n\to H(z)z^n$

于是，在LTI系统下，单位脉冲响应为$h(t)$，当输入信号$x(t)$，得到的响应$y(t)$

$y(t)=\int_{-\infin}^{+\infin}h(\tau)x(t-\tau)d\tau \ =\int_{-\infin}^{{+\infin}h(\tau)e}{s(t-\tau)}\ =e^{{st}\int_{-\infin}}{+\infin}h(\tau)e^{-s\tau}d\tau $

也就是$y(t)=H(s)e^{st}$

系统函数 System Function

$H(s)=\int_{-\infin}^{{+\infin}h(\tau)e}{-s\tau}d\tau $

$H(z)={\Sigma }_{-\infty }^{+\infty }h[k]z^{-k}$

这实际上使得傅立叶级数的分析理论更完备了。因为我们现在要表示一个系统，已经可以抛开时域，关注频域，利用系统函数来表示LTI系统。那就有根据输入求输出的公式：

$x(t)={\Sigma }_{-\infty }^{+\infty }{a}_k{e}^{jk{\omega }_{0}t}$

$y(t)={\Sigma }_{-\infty }^{+\infty }{a}_{k}H(jk{\omega }_0)e^{jk{\omega }_{0}t}$

那就有根据输入输出反求系统函数的方式。这在傅立叶变换中更显作用。