最优化方法——Newton方法

1. 问题介绍

        在最优化方法中，Newton方法是一个比较经典的方法，它常用来求解无约束的优化问题或含有等式约束的优化问题。准确的说，Newton方法一般分为纯Newton方法和拟Newton方法。今天我们考虑的是无约束优化问题的纯Newton方法，其他衍生方法后续再讲解。
        求解的问题是：$\min f(x)$

        迭代方法的基本思想：我们每次都按一个方向找一个点$x^{(i)}$（$i$表示第$i$次迭代时找的点），如果每次点对应的函数值都小于前一次，即$f(x^{(i+1)})<f(x^{(i)})$，那么我们总能找到最终需要的点$x^{\ast }$，该点处函数值是最小的。
        根据上面的思想，我们需要做的只有两点：一是往哪个方向找点；二是找到方向后，你应该以什么样的规则去确定要找的点，也即是步长。目前我们所了解的绝大部分迭代优化算法都是围绕方向和步长这两点来做文章。
        例子：不一定恰当，但有助于你理解。想像一下你在登一座未开发的山，你的目标是找到山的最高点（你把山倒过来看，那么最高点就是我们要的$x^{\ast }$）。首先你要做的是确定从哪个方向登山，因为有的方向路线比较陡峭，有的方向比较平坦，陡峭的方向当然有助于你快速到达最高点。其次你要做的是确定每步跨多大，即步长。如果你每步都是2米的步长去走，虽然你会以更快的速度接近你要的点，但也很有可能越过最高点。

2. Newton方向的解释与推导

        根据上面迭代的基本思想，Newton方法之所以叫Newton方法，因为他找了一个方向，该方向称之为Newton方向。那么何为Newton方向方向呢？

2.1 二阶近似角度

        假设迭代到第k步，点从$k-1$步的$x^{(k-1)}=x$ 变为 $x^{(k)}=x+v$，此时函数值为 $f(x+v)$，其二阶Taylor近似为：
$$f(x+v)\approx \hat{f}(x+v)=f(x)+\nabla f(x{)}^{T}v+\frac{1}{2}{v}^T{\nabla }^{2}f(x)v$$ 显然，上式是关于$v$的二次凸函数。如果在点$x^{(k)}$处函数值最小，那么应该有其一阶导等于0。因此，我们对$v$求一阶偏导并令其等于0有：
$$\nabla f(x)+{\nabla }^{2}f(x)v=0$$求得$v$等于：$v=-[{\nabla }^{2}f(x){]}^{-1}\nabla f(x)$。好了，$-[{\nabla }^{2}f(x){]}^{-1}\nabla f(x)$即为牛顿方向，记为$\Delta x_{nt}$。（注意：方向一定是个向量）
通过上述分析，我们可以看出 牛顿方向的一些本质。具体见下图：

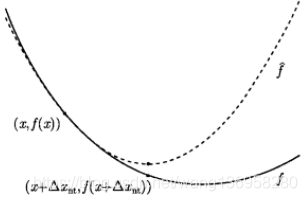
上图中，实线是实际的函数，虚线是该函数的二阶近似，我们可以直观的看出，如果$f$是二次的，那么$x+\Delta x_{nt}$就是最优点$x^{\ast }$,即使$f$不是二次的，当$x$靠近$x^{\ast }$时，$x+\Delta x_{nt}$也是$x^{\ast }$的一个比较好的估计。

2.2 线性化最优性条件的角度

        我们知道对于可微函数，其最优解的充分条件是$x^{\ast }$处的梯度为0，即$\nabla f(x^{\ast })$，我们对其进行线性化（即一阶展开）：$$\nabla f(x+v)\approx \nabla f(x)+{\nabla }^{2}f(x)v=0$$同样我们可以求得$v=-[{\nabla }^{2}f(x){]}^{-1}\nabla f(x)$，即$\Delta x_{nt}$。
注：牛顿方向具有仿射不变性，此处就不细讲了。

3. Newton减量

        我们将$\lambda (x)=(\nabla f(x{)}^T[{\nabla }^{2}f(x){]}^{-1}\nabla f(x){)}^{\frac{1}{2}}$称为$x$处的Newton减量。减量的作用在于设计迭代的停止准则。我们有：

f ( x ) − f ^ ( x + v ) = f ( x ) − f ( x ) − ∇ f ( x ) T v − 1 2 v T ∇ 2 f ( x ) v = − ∇ f ( x ) T { − [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) } − 1 2 { − [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) } T ∇ 2 f ( x ) { − [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) } = ∇ f ( x ) T [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) − 1 2 ∇ f ( x ) T { [ ∇ 2 f ( x ) ] − 1 } T ∇ 2 f ( x ) [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) = ∇ f ( x ) T [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) − 1 2 ∇ f ( x ) T [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) = 1 2 ∇ f ( x ) T [ ∇ 2 f ( x ) ] − 1 ∇ f ( x ) = 1 2 λ ( x ) 2 f(x) - \hat f(x+v) = f(x) - f(x)-\nabla f{(x)^T}v - \frac{1}{2}{v^T}{\nabla ^2}f(x)v \\ =-\nabla f{(x)^T}\{- [{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x) \}-\frac{1}{2}\{- [{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x) \}^T {\nabla ^2}f(x)\{- [{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x) \} \\ =\nabla f{(x)^T}[{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x)-\frac{1}{2}\nabla f(x)^{T} \{ [{\nabla ^2}f{(x)]^{ - 1}}\}^T{\nabla ^2}f(x) [{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x) \\ =\nabla f{(x)^T}[{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x)-\frac{1}{2}\nabla f{(x)^T}[{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x)\\ =\frac{1}{2}\nabla f{(x)^T}[{\nabla ^2}f{(x)]^{ - 1}}\nabla f(x) =\frac{1}{2}\lambda {(x)^2} f(x)−f^​(x+v)=f(x)−f(x)−∇f(x)Tv−21​vT∇2f(x)v=−∇f(x)T{−[∇2f(x)]−1∇f(x)}−21​{−[∇2f(x)]−1∇f(x)}T∇2f(x){−[∇2f(x)]−1∇f(x)}=∇f(x)T[∇2f(x)]−1∇f(x)−21​∇f(x)T{[∇2f(x)]−1}T∇2f(x)[∇2f(x)]−1∇f(x)=∇f(x)T[∇2f(x)]−1∇f(x)−21​∇f(x)T[∇2f(x)]−1∇f(x)=21​∇f(x)T[∇2f(x)]−1∇f(x)=21​λ(x)2
其中，第二个等号是将$v$值代入进去，第三个等号涉及$(AB{)}^T=B^T{A}^T$矩阵转置知识，第四个等号涉及$[{\nabla }^{2}f(x){]}^{-1}$是一个对称阵，对称阵的转置等于其本身。因此，$\frac{1}{2}\lambda (x{)}^2$是对$f(x)-f(x^{(k)})$的估计值，即我们可以将其作为迭代停止条件：当$\frac{1}{2}\lambda (x{)}^2⩽\epsilon$时，说明第$k$步迭代的函数与上次相比差距非常小了，迭代结果已经非常接近函数的最小值了，迭代可以停止。
——————————————————————————————
Newton 算法
（1） 给定初始点 $x\in domf$, 误差阈值 $\epsilon$;
（2） 计算Newton方向和步长：
$$\Delta x_{nt}=-\nabla f(x)[{\nabla }^{2}f(x){]}^{-1}；$$
$$\lambda (x{)}^2=\nabla f(x{)}^T[{\nabla }^{2}f(x){]}^{-1}\nabla f(x);$$
（3） 停止准则：如果$\frac{1}{2}\lambda (x{)}^2⩽\epsilon$时，退出，否则进入下一步；
（4） 确定步长$t$：通过线性搜索或Armijo Rule搜索；
（5） 进入下一步迭代：$x=x+t\Delta x_{nt}$
（6）重复进行直至达到停止条件。
————————————————————————————
注意：我们一般称步长$t=1$时，为纯Newton方法。
以上就是最为基础的Newton算法的原理，可以注意到，该方法的一个主要特点是要求海塞矩阵${\nabla }^{2}f(x)$可逆，因此如果某点处的海塞矩阵是奇异矩阵（即不可逆。虽然海塞矩阵是对称阵，但其特征值并非全部都是非零的），那么该方法将会失去效用，正因为如此，才有了后续的拟Newton方法。

4. 收敛性分析

        关于Newton方法的收敛性分析（此处我们需要假定函数二次连续可微且具有强凸性）比较复杂。在此，我们只给出一些直观的结论，具体证明请查找相关书籍。
在介绍收敛性结论之前，先介绍关于$Lipschitz$连续。我们说一个函数$f$是以$L$为常数的$Lipschitz$连续的，即$${\Vert f(x)-f(y)\Vert }_2⩽L{\Vert x-y\Vert }_2$$对任意的$x,y\in domf$都成立，其中$L$称$Lipschitz$常数。该连续是一种比较强的连续，函数有比较好的光滑性，因为上式要求函数值得变化是缓的。对于Newton方法的收敛性分析，我们还需要假设其海塞矩阵${\nabla }^{2}f(x)$是$Lipschitz$连续的。
下面我们将说明Newton方法的收敛性结论：存在满足$0<\eta ⩽\frac{m^2}{L}$和$\gamma >0$的$\eta$和$\gamma$使下式成立：
（1）如果${\Vert \nabla f(x^{(k)})\Vert }_2⩾\eta$,则$${\Vert \nabla f(x^{(k+1)})-f(x^{(k)})\Vert }_2⩽-\gamma$$
（2）如果${\Vert \nabla f(x^{(k)})\Vert }_2⩽\eta$，则用Armijo搜索产生的$t^{(k)}=1$，且有$$\frac{L}{2m^2}{\Vert \nabla f(x^{(k+1)})\Vert }_2⩽{\left(\frac{L}{2m^2}{\Vert \nabla f(x^{(k)})\Vert }_2\right)}^2$$
上述两个式子其实，描述了Newton方法收敛的两个阶段：第一个式子描述的是收敛速度较慢的阶段，我们一般称之为阻尼Newton阶段；第二个式子描述的是收敛速度非常快的的阶段，也我们常说的搜索点靠近最优点了，我们一般称之为二次收敛阶段，该阶段一般迭代次数大体上不会超过6次。
上述两个不等式的证明较为复杂，此处不做详细证明了。我们给出上式中一些参数的取值：
$\gamma =\alpha \beta {\eta }^2\frac{m}{M^2}$， η = min ⁡ { 1 , 3 ( 1 − 2 α ) } m 2 L \eta = \min \left\{ {1,3(1 - 2\alpha )} \right\}\frac{{{m^2}}}{L} η=min{1,3(1−2α)}Lm2​
其中，$\alpha$和$\beta$分别表示Armijo搜索方法中的两个参数，$m$和$M$是函数强凸性中的参数，即$mI\preccurlyeq {\nabla }^{2}f(x)\preccurlyeq MI$；$L$是$Lipschitz$常数。
————————————————————————————
总结： Newton方法的核心在于Newton方向，该方向我们可以从二阶近似的角度去推导，当步长为1时，我们称之为纯Newton方法；其次，通过收敛性分析，我们知道当搜索点靠近最优点时，Newton方法具有非常快的收敛速度（二次收敛），具有较好的性质，但同时我们也需要注意到其缺点：一是Newton方向中含有海塞矩阵的可逆矩阵，因此要求在当前点的海塞矩阵是非奇异的；二是当搜索点离最优点比较远时（即在阻尼Newton阶段），收敛速度将会非常慢（比线性收敛还慢）；也正是有此缺点，才有了后续的一些拟Newton方法。