leetcode 2421. Number of Good Paths（python）-CSDN博客

本文链接：https://blog.csdn.net/wang7075202/article/details/140826555

leetcode 2421. Number of Good Paths（python）

描述

There is a tree (i.e. a connected, undirected graph with no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the i^th node. You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A good path is a simple path that satisfies the following conditions:

The starting node and the ending node have the same value.
All nodes between the starting node and the ending node have values less than or equal to the starting node (i.e. the starting node’s value should be the maximum value along the path).

Return the number of distinct good paths.

Note that a path and its reverse are counted as the same path. For example, 0 -> 1 is considered to be the same as 1 -> 0. A single node is also considered as a valid path.

Example 1:

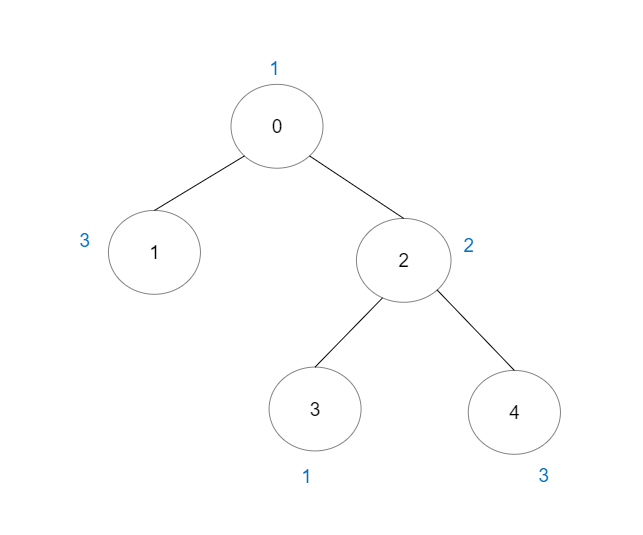
Input: vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
Output: 6
Explanation: There are 5 good paths consisting of a single node.
There is 1 additional good path: 1 -> 0 -> 2 -> 4.
(The reverse path 4 -> 2 -> 0 -> 1 is treated as the same as 1 -> 0 -> 2 -> 4.)
Note that 0 -> 2 -> 3 is not a good path because vals[2] > vals[0].

Example 2:

Input: vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
Output: 7
Explanation: There are 5 good paths consisting of a single node.
There are 2 additional good paths: 0 -> 1 and 2 -> 3.

Example 3:

Input: vals = [1], edges = []
Output: 1
Explanation: The tree consists of only one node, so there is one good path.

Note:

n == vals.length
1 <= n <= 3 * 10^4
0 <= vals[i] <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.

解析

根据题意，有一棵树由 n 个节点组成，编号从 0 到 n - 1 ，正好有 n - 1 条边。给定一个长度为 n 的 0 索引的整数数组 vals ，其中 vals[i] 表示第 i 个节点的值。另外给出一个二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示存在连接节点 a_i 和 b_i 的无向边。

一条好的路径得满足以下条件：

起始节点和结束节点具有相同的值。
起始节点和结束节点之间的所有节点的值都小于或等于起始节点，即起始节点的值应为路径上的最大值。

返回不同良好路径的数量。请注意，路径与其反向路径被认为是同一路径。例如，0 -> 1 被视为与 1 -> 0 相同。单个节点也被视为有效路径。

这道题我也是看了大佬的讲解才想明白的，主要思路就是将这个树的问题转换成了图的问题，使用了并查集来解决该题。

最开始我们将这棵树中的节点都单独拿出来，想象他们彼此都是没有联系的，此时也就是一个有 N 个节点的没有互相联系的图，此时已经有 N 条有用的路径出现了，加入到 result 中，也就是每个节点自身。然后由于每个有用的路径都是起始节点相同且大于等于中间的节点值，所以我们在图中最先找出现值最小的节点 x ，这样可以始终保证连通块的代表元的节点值是最大的。对于节点 x 及其邻居 y ，如果 y 所处的连通分量的最大节点值不超过 vals[x] ，那么可以把 y 所处的连通块合并到 x 所处的连通块中。如果此时这两个连通块的最大节点值相同，那么可以根据乘法原理，把这两个连通块内的等于最大节点值的节点个数相乘，加到答案 result 中，不断遍历累积计算最终得到结果。

时间复杂度为 O(NlogN) ，空间复杂度为 O(N)。

解答

class Solution(object):
    def numberOfGoodPaths(self, vals, edges):
        """
        :type vals: List[int]
        :type edges: List[List[int]]
        :rtype: int
        """
        def find(x):
            if father[x] != x:
                father[x] = find(father[x])
            return father[x]

        n = len(vals)
        graph = [[] for _ in range(n)]
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        father = list(range(n))
        L = [1] * n
        result = n
        for val, x in sorted(zip(vals, range(n))):
            father_x = find(x)
            for y in graph[x]:
                y = find(y)
                if y == father_x or vals[y] > val:
                    continue
                if vals[y] == val:
                    result += L[father_x] * L[y]
                    L[father_x] += L[y]
                father[y] = father_x
        return result

运行结果

Runtime 1715 ms，Beats 88.69%
Memory 53.3 MB，Beats 18.35%

原题链接

https://leetcode.com/problems/number-of-good-paths/description/

您的支持是我最大的动力