pcl把3dmesh 映射成2维_Manytasking Jmetal 代码反向解析 2_MMDTLZ

MATP与MMDTLZ优化问题解析：旋转矩阵与决策变量映射
于 2020-12-15 04:13:36 发布
阅读量160 收藏
点赞数
CC 4.0 BY-SA版权
文章标签： pcl把3dmesh 映射成2维
原文链接：https://blog.csdn.net/u013555719/article/details/103617911
本文详细分析了MATP（Many Task Optimization Problem）中MMDTLZ（Multi-objective Many-task Test Problem）的实现，特别是旋转矩阵在决策变量空间变换中的作用。通过MATP1实例，解释了如何通过设置目标数、决策变量数、旋转矩阵和偏移向量来构建和评估多任务优化问题。旋转矩阵用于复杂化函数映射关系，而transformVariables函数则负责将解的决策变量从[0,1]区间映射到原始问题空间，并进行旋转和偏移。evalG函数计算目标函数，涉及DTLZ4的评价方法。整个过程展示了多目标优化问题的数学建模和求解步骤。

觉得有用的话,请点击右下角fde2304593d29ef6246aa14275e4473a.gif

推荐给更多小伙伴 8ada0334360b8e74aaff6fde38b7e4be.pngneoken_xu5c040625d32d9934fabd569c1b824a94.pngAsurada2015cb256ad2f49ab56a575aed4dac7af5ee.pngEvacloud

  • 这是我在写 Manytask optimization 时的笔记，代码地址可以下载[1]
    “

    相关文献[1]反向解析\_1 Manytasking optimization MATP[2] >[2]旋转矩阵[3] >[3]Jmetal Problem 和 Problem Set 的变量范围[4] >[4]MATP ManyTask Multitask Problem 和 Solution 的变量范围[5] >[5]MATP1 生成测试 SolutionSet[6] >[6]Manytasking MATP MOOMFO 中 G 函数[7]

MMDTLZ 代码

  • 根据参考文献[1],可知 MATP1 是根据 MMDTLZ 函数测试集写的
//MATP1
MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100);
  prob.setGType("sphere");
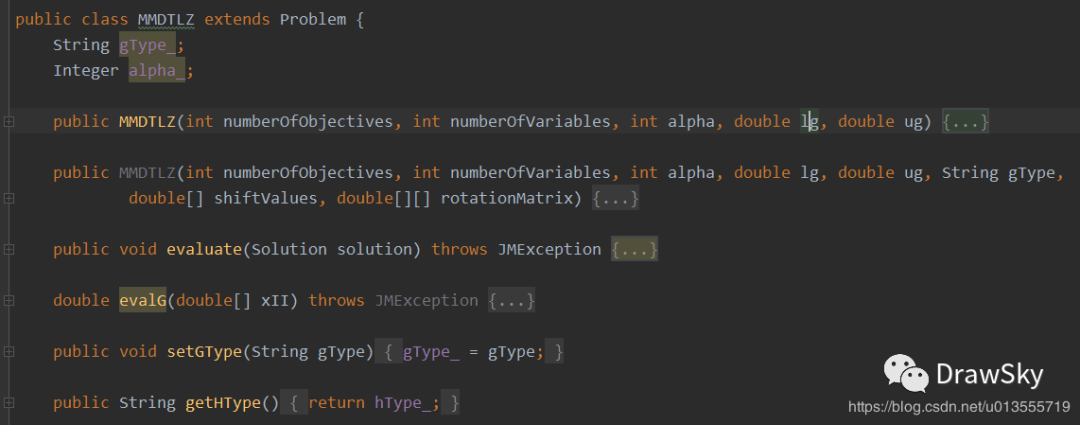
  • 打开 MMDTLZ，0b7c21b7af7fd744b4f3064d969bfe33.png
  • 发现其有两个初始化函数，但是只有上面的经常使用，evaluate,和 evalG 两个评价函数，还有两个设置函数 setGType 和 GetHType
public MMDTLZ(int numberOfObjectives, int numberOfVariables, int alpha, double lg, double ug) {
  numberOfObjectives_ = numberOfObjectives;
  numberOfVariables_ = numberOfVariables;

  gType_ = "sphere";

  alpha_ = alpha;

  int num = numberOfVariables_ - numberOfObjectives_ + 1;

  // System.out.println(num);

  shiftValues_ = new double[num];
  rotationMatrix_ = new double[num][num];

  upperLimit_ = new double[numberOfVariables_];
  lowerLimit_ = new double[numberOfVariables_];

  for (int var = 0; var 1; var++) {
    lowerLimit_[var] = 0.0;
    upperLimit_[var] = 1.0;
  } // for

  for (int var = numberOfObjectives_ - 1; var var++) {
    lowerLimit_[var] = lg;
    upperLimit_[var] = ug;
  }

  for (int i = 0; i     shiftValues_[i] = 0;

  for (int i = 0; i     for (int j = 0; j       if (i != j)
        rotationMatrix_[i][j] = 0;
      else
        rotationMatrix_[i][j] = 1;
    }
  }

  if (numberOfObjectives == 2)
    hType_ = "circle";
  else
    hType_ = "sphere";
}

以 MATP1 分析 MMDTLZ 的初始化

//MATP1
MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100);
  prob.setGType("sphere");
  • numberOfObjectives=2
  • numberOfVariables=50
  • alpha=1
  • lg=-100
  • ug=100
  • gType_ = "sphere";
public MMDTLZ(int numberOfObjectives, int numberOfVariables, int alpha, double lg, double ug) {
      numberOfObjectives_ = numberOfObjectives;
      numberOfVariables_ = numberOfVariables;

      gType_ = "sphere";

//  MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100);
//  prob.setGType("sphere");

      alpha_ = alpha;

      int num = numberOfVariables_ - numberOfObjectives_ + 1;
      //以MATP1为例
      //num=50-2+1=49


      // System.out.println(num);

      shiftValues_ = new double[num];//49
      rotationMatrix_ = new double[num][num];//(49,49)

      upperLimit_ = new double[numberOfVariables_];//50
      lowerLimit_ = new double[numberOfVariables_];//50

      for (int var = 0; var 1; var++) {
          lowerLimit_[var] = 0.0;
          upperLimit_[var] = 1.0;
      } // for
      //初始化将(目标值维度-1)的决策变量数值范围限制在0-1之间,即如果是一个双目标问题，则只有x_0即第一个决策变量的值是0-1的范围之间

      for (int var = numberOfObjectives_ - 1; var var++) {
          lowerLimit_[var] = lg;
          upperLimit_[var] = ug;
      }
      //对于1-49维度的值上下界都根据问题进行指定，例如此处为MATP1问题则(-100,100)之间

      for (int i = 0; i           shiftValues_[i] = 0;
      //0-48维shiftValues_数值初始化为0

      for (int i = 0; i           for (int j = 0; j               if (i != j)
                  rotationMatrix_[i][j] = 0;
              else
                  rotationMatrix_[i][j] = 1;
          }
      }
      //对于这个49*49维度的矩阵非对角线上的值设置为0，对角线上的值设置为1

      if (numberOfObjectives == 2)
          hType_ = "circle";//由与Manytasking的优化问题，目标数都为2，因此hType_为都"circle"
      else
          hType_ = "sphere";
  }
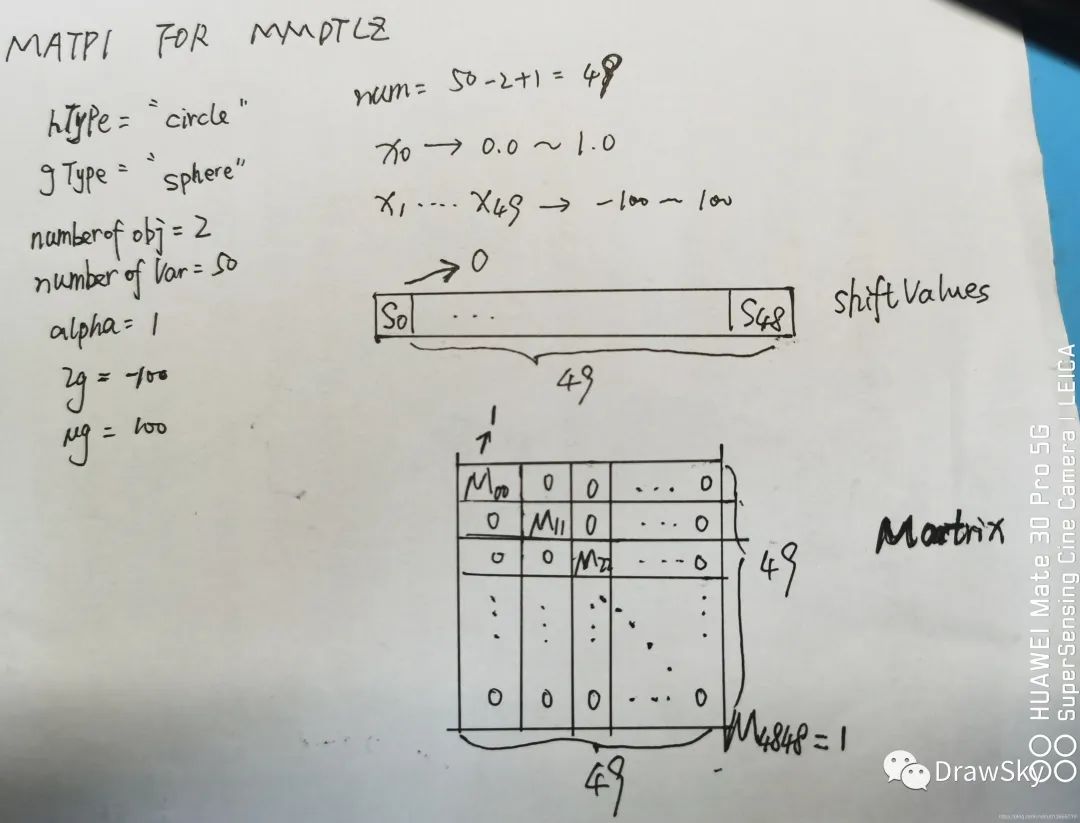
93fe3ad061258f84eb448b6ffa17ea3e.png

基于 MATP1 使用旋转矩阵理解 MMDTLZ

没有什么比画几个对比图更加让人容易理解旋转矩阵在 MMDTLZ 中的应用了--呵呵

  • 根据 MATP1 中的 getT 函数
ProblemSet problemSet = new ProblemSet(1);

  MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100);
  prob.setGType("sphere");


  double[][] matrix = IO.readMatrixFromFile("MData/M1/M1_"+taskID+".txt");

  double shiftValues[] = IO.readShiftValuesFromFile("SVData/S1/S1_"+taskID+".txt");

  prob.setRotationMatrix(matrix);
  prob.setShiftValues(shiftValues);

  ((Problem)prob).setName("MATP1-"+taskID);

  problemSet.add(prob);

  return problemSet;
  • 可知不同的旋转矩阵是通过reandMatrixFromFile函数读取的,偏移向量是通过readShiftValuesFromFile函数读取的

旋转矩阵

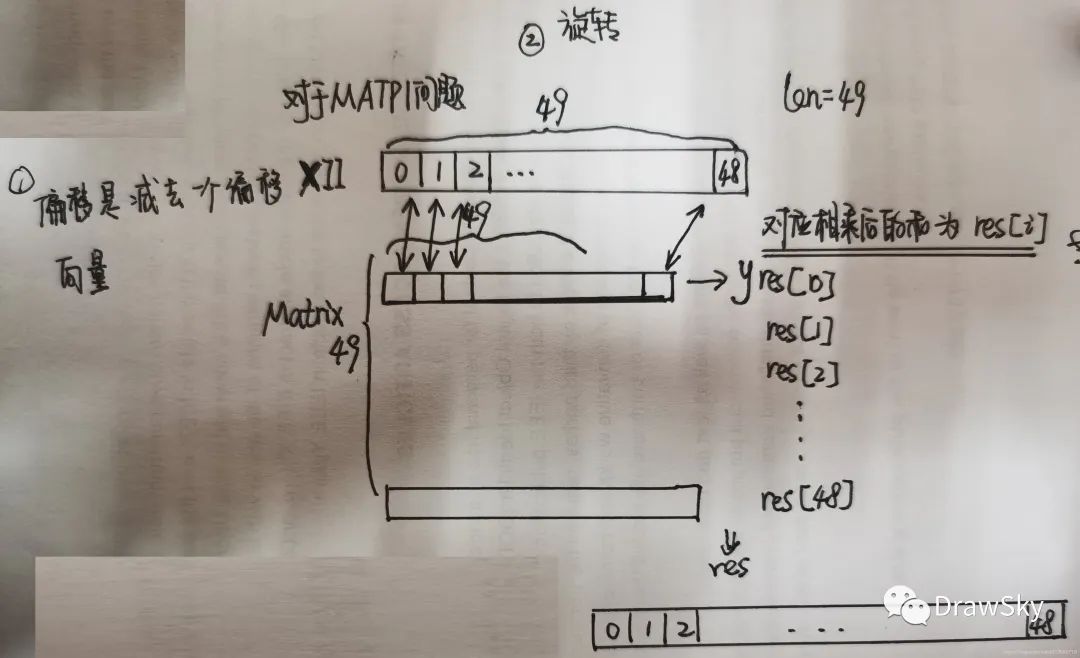
  • 对于多任务问题中，MATP1 中 50 个不同的任务实质上是通过旋转矩阵 A 和偏移向量 B 这两个在 DTLZ 问题上进行改变得出的，旋转矩阵和偏移向量的关系其实是为了将函数映射的关系复杂化。[旋转矩阵][8]
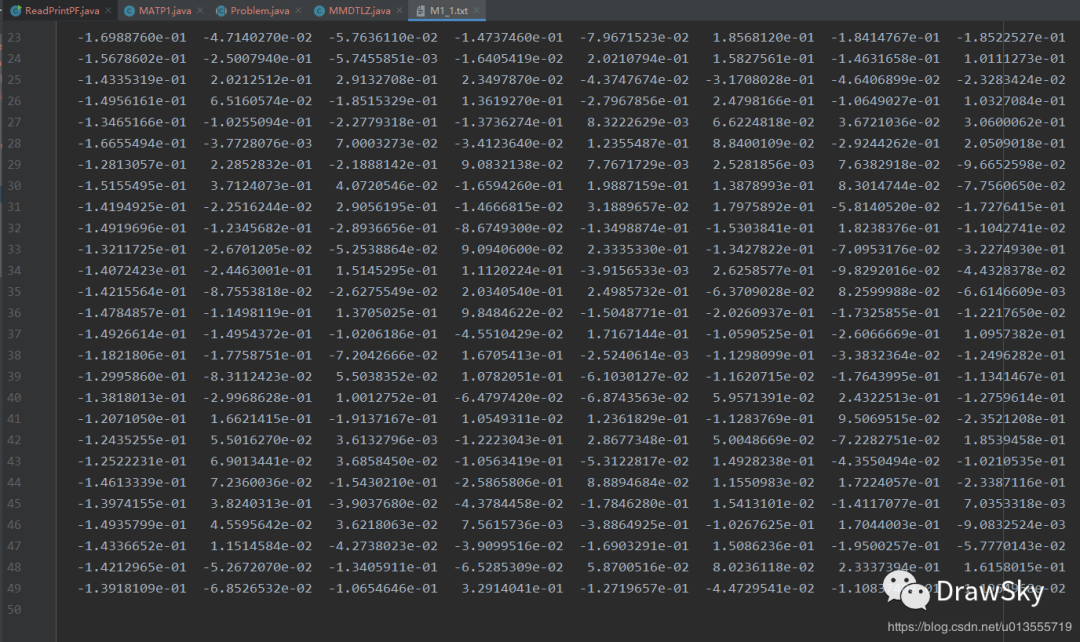
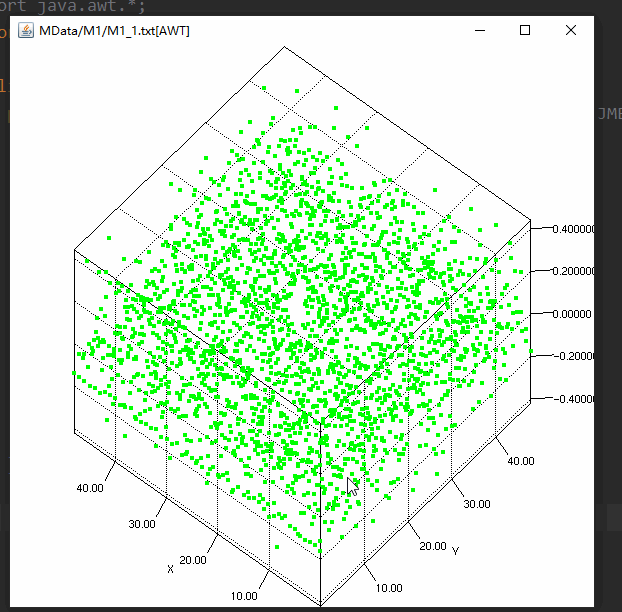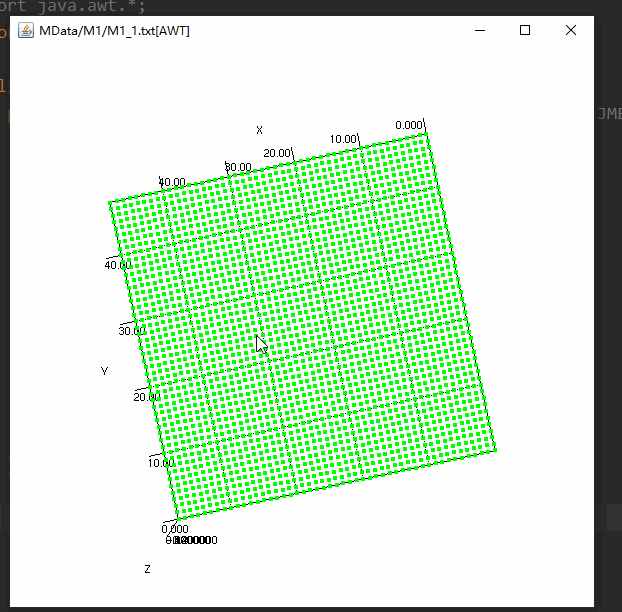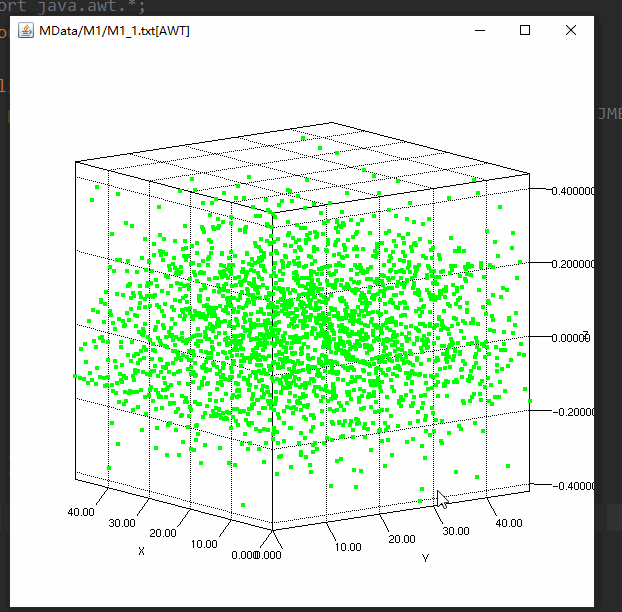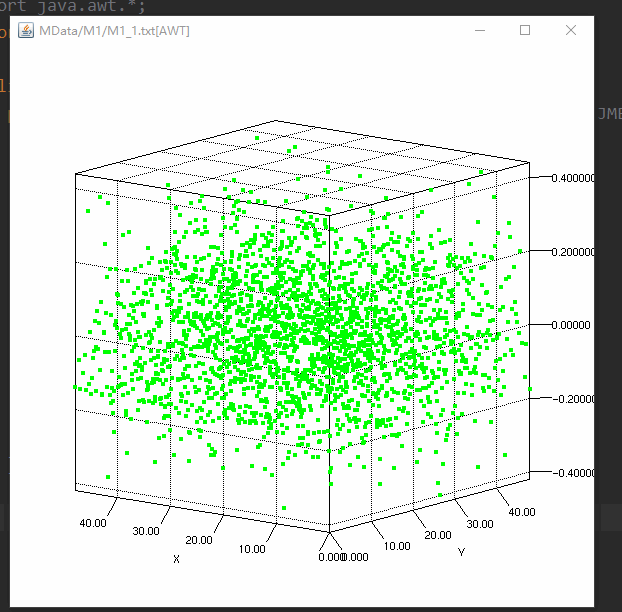
  • 但是但看 M1.txt 这个 49*49 维度的矩阵看的我是一脸懵逼acc57240e7bc15da692e1b3660da96eb.png150b144480b43e76914357d5a7272cde.gife37a56549312019e2d141426d9ec543f.png97729bc2f8454a6e8ca457cf75c2b126.png

这是因为对于这个 49*49 的矩阵，应该将其视为 49 个行向量来重新映射决策变量空间，每个行向量都重新定义了旋转以后的坐标轴，每一行的对应元素和 Solution 中的对应维度相乘后相加得到的结果为新的 solution 中对应维度值

bc4b15881d6b50f574de9876860e41fd.png

MMDTLZ evaluate 函数

使用 scaleVariables(solution)函数将解的决策变量从[0,1]映射到原有的空间

“

[3]Jmetal Problem 和 Problem Set 的变量范围[9] >[4]MATP ManyTask Multitask Problem 和 Solution 的变量范围[10] >[5]MATP1 生成测试 SolutionSet[11]

1b7b6912a69029c6fa1f0ef9c1ce6035.png
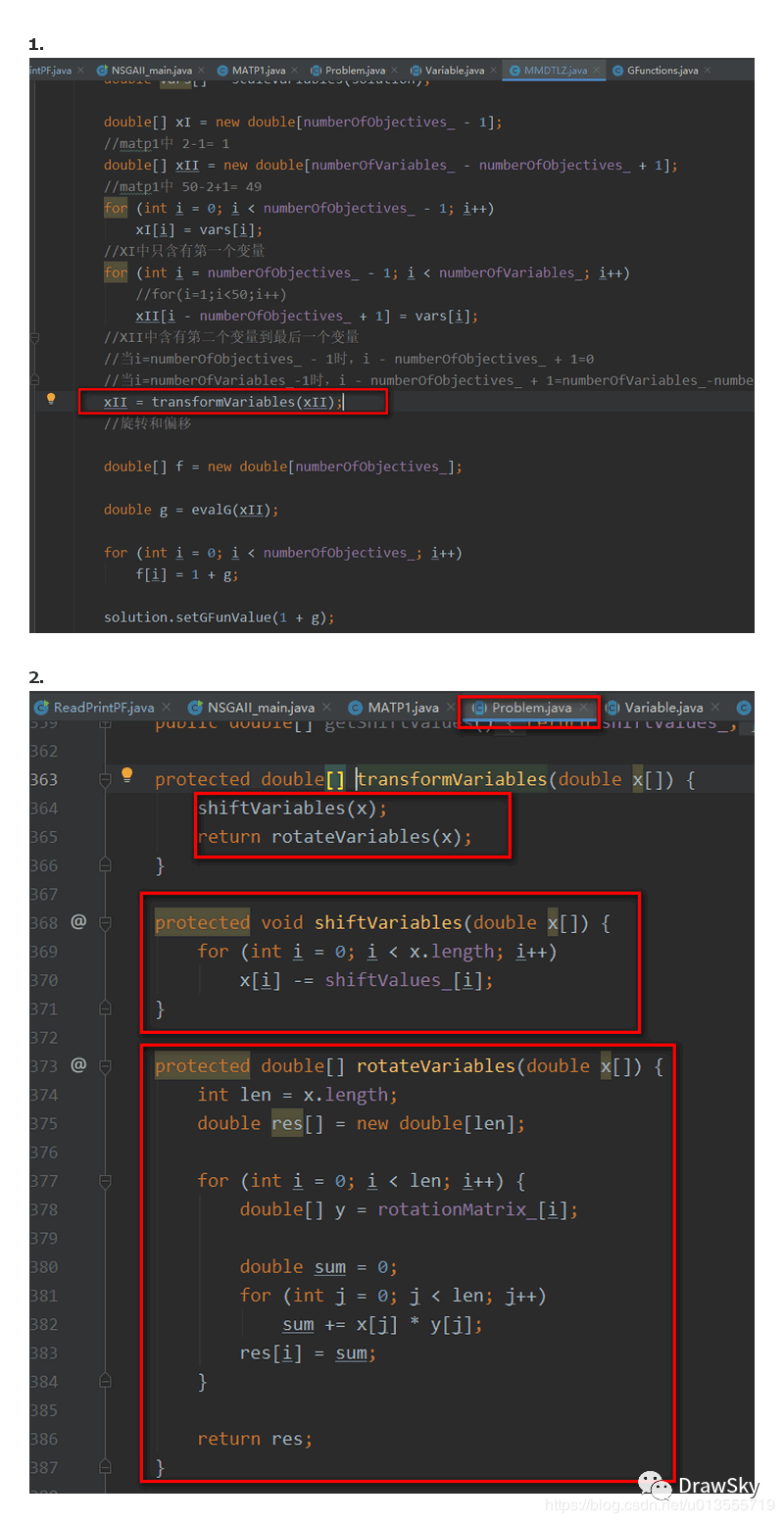
public void evaluate(Solution solution) throws JMException {
        double vars[] = scaleVariables(solution);

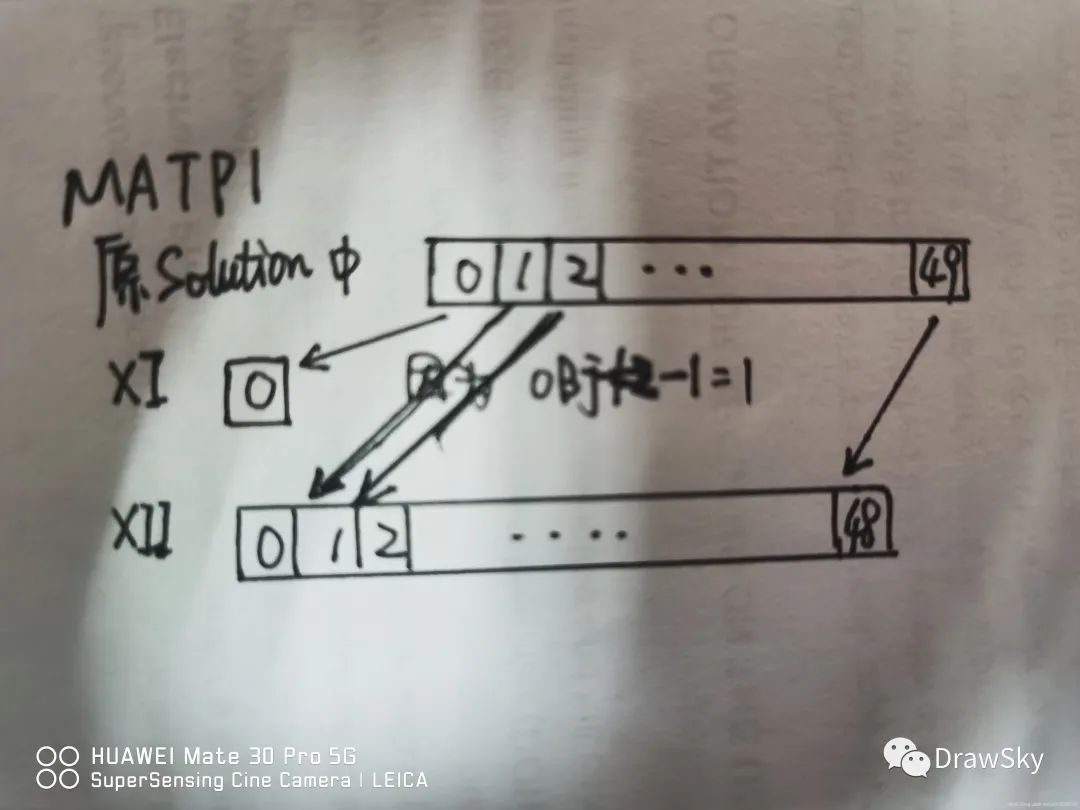
        double[] xI = new double[numberOfObjectives_ - 1];
        //matp1中 2-1= 1
        double[] xII = new double[numberOfVariables_ - numberOfObjectives_ + 1];
        //matp1中 50-2+1= 49
        for (int i = 0; i 1; i++)
            xI[i] = vars[i];
        //XI中只含有第一个变量
        for (int i = numberOfObjectives_ - 1; i             //for(i=1;i<50;i++)
            xII[i - numberOfObjectives_ + 1] = vars[i];
        //XII中含有第二个变量到最后一个变量
        //当i=numberOfObjectives_ - 1时，i - numberOfObjectives_ + 1=0
        //当i=numberOfVariables_-1时，i - numberOfObjectives_ + 1=numberOfVariables_-numberOfObjectives_=48 其实是第49个变量
        xII = transformVariables(xII);
        //旋转和偏移

        double[] f = new double[numberOfObjectives_];

        double g = evalG(xII);

        for (int i = 0; i             f[i] = 1 + g;

        solution.setGFunValue(1 + g);

        for (int i = 0; i             for (int j = 0; j 1); j++)
                f[i] *= Math.cos(Math.pow(xI[j], alpha_) * 0.5 * Math.PI);
            if (i != 0) {
                int aux = numberOfObjectives_ - (i + 1);
                f[i] *= Math.sin(Math.pow(xI[aux], alpha_) * 0.5 * Math.PI);
            } // if
        } // for

        for (int i = 0; i             solution.setObjective(startObjPos_ + i, f[i]);
    }

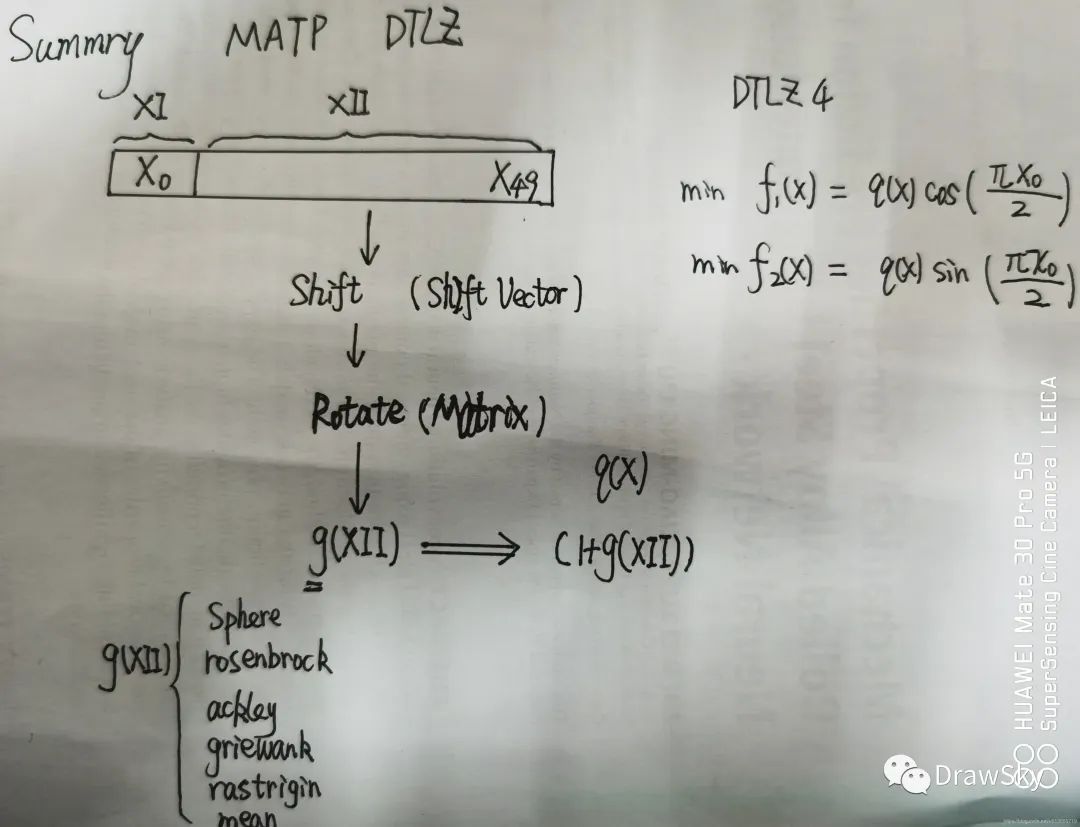
xII = transformVariables(xII)是用于旋转和偏移的函数，总体而言前面的代码就是将 0-1 空间恢复到问题空间，然后将决策变量拆分为 XI 和 XII

95f5db0dc12c089f6eca31610066128a.png

transformVariables

xII = transformVariables(xII);
//跳转到Problem父类中的transformVariables函数，因为MMDTLZ本身就是Problem的子类
protected double[] transformVariables(double x[]) {
   shiftVariables(x);
   return rotateVariables(x);
   //先进行偏移，然后进行旋转
 }
protected void shiftVariables(double x[]) {
 for (int i = 0; i    x[i] -= shiftValues_[i];
}

protected double[] rotateVariables(double x[]) {
  int len = x.length;
  double res[] = new double[len];

  for (int i = 0; i     double[] y = rotationMatrix_[i];

    double sum = 0;
    for (int j = 0; j       sum += x[j] * y[j];
    res[i] = sum;
  }

  return res;
}
ba3c020b010cfba25866f3675429e8ac.png

evalG(xII)

使用 Gfunction 对原有决策变量进行处理

“

Manytasking MATP MOOMFO 中 G 函数[12]

计算目标函数

  • 设置 Solution G 函数
for (int i = 0; i    f[i] = 1 + g;

solution.setGFunValue(1 + g);
  • 计算目标函数
//本质是一个DTLZ4的评价函数计算方法
//1. 此时f[i]中保存着(1+g)的值
//2. 对于MATP中的所有问题而言，目标函数的个数是两个，所以numberOfobjective=2
//i=0时, numberOfObjectives_ - (i + 1)=2-1=1 j<1 即j=0,即j只会等于0
//i=1时，numberOfObjectives_ - (i + 1)=2-2=0 j<0 此时不会进入for循环而直接进入if语句，
//      aux = numberOfObjectives_ - (i + 1)=2-(2)=0
//alpha=1

for (int i = 0; i   for (int j = 0; j 1); j++)
    f[i] *= Math.cos(Math.pow(xI[j], alpha_) * 0.5 * Math.PI);
  if (i != 0) {
    int aux = numberOfObjectives_ - (i + 1);
    f[i] *= Math.sin(Math.pow(xI[aux], alpha_) * 0.5 * Math.PI);
  } // if
} // for

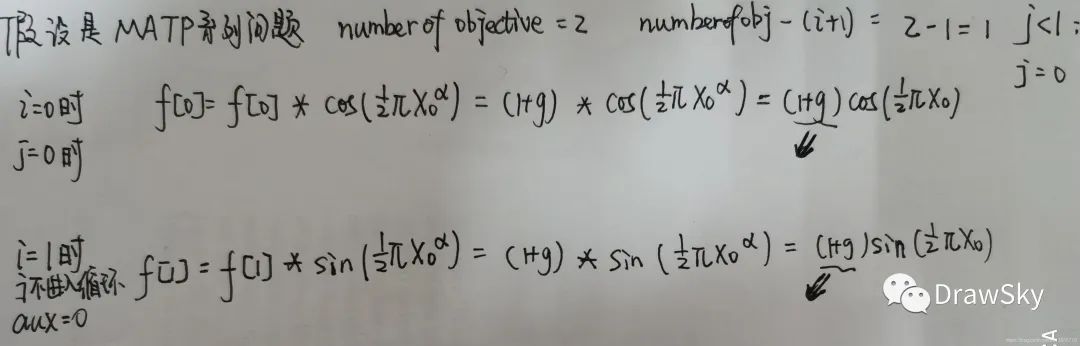
26892e62faa3691154b0fb7aa963cc4c.png86a198ab44f9d019357d680294251cac.png

总结：使用 DTLZ 系列构造 MATP 问题的评价函数

1f9a7874f427d96fbd13f016c669189e.png

参考资料

[1]

地址可以下载: http://www.bdsc.site/websites/MTO/MO-ManyTask-Benchmarks.rar

[2]

[1]反向解析_1 Manytasking optimization MATP: https://blog.csdn.net/u013555719/article/details/103569252

[3]

[2]旋转矩阵: https://www.cnblogs.com/zhoug2020/p/7842808.html

[4]

[3]Jmetal Problem和Problem Set的变量范围: https://blog.csdn.net/u013555719/article/details/103595998

[5]

[4]MATP ManyTask Multitask Problem和Solution的变量范围: https://blog.csdn.net/u013555719/article/details/103599862

[6]

[5]MATP1生成测试SolutionSet: https://blog.csdn.net/u013555719/article/details/103603894

[7]

[6]Manytasking MATP MOOMFO 中G函数: https://blog.csdn.net/u013555719/article/details/103615605

[8]

[旋转矩阵]: https://www.cnblogs.com/zhoug2020/p/7842808.html

[9]

[3]Jmetal Problem和Problem Set的变量范围: https://blog.csdn.net/u013555719/article/details/103595998

[10]

[4]MATP ManyTask Multitask Problem和Solution的变量范围: https://blog.csdn.net/u013555719/article/details/103599862

[11]

[5]MATP1生成测试SolutionSet: https://blog.csdn.net/u013555719/article/details/103603894

[12]

Manytasking MATP MOOMFO 中G函数: https://blog.csdn.net/u013555719/article/details/103615605

豪欧巴
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值