1、基本概念:PageRank 是基于【从许多优质的网页链接过来的网页,必定还是优质网页】的回归关系,来判定所有网页的重要性
2、具体算法:将某个页面的 PageRank 除以存在于这个页面的正向链接,由此得到的值分别和正向链接所指向的页面的 PageRank 相加,即是被链接的页面的 PageRank。
3、PageRank概念图:

4、PageRank的要点:
反向链接数 (单纯的意义上的受欢迎度指标)
反向链接是否来自推荐度高的页面 (有根据的受欢迎指标)
反向链接源页面的链接数 (被选中的几率指标)
5、例子来说明PageRank的具体过程
假设一个由4个页面组成的小团体:A、B、C、D。如果所有页面都链向A,那么A的PR(PageRank)值将是B,C及D的和。
PR(A) = PR(B) + PR(C) + PR(D)
继续假设B也有链接到C,并且D也有链接到包括A的3个页面。一个页面不能投票2次。所以B给每个页面半票。以同样的逻辑,D投出的票只有三分之一算到了A的PageRank上。
PR(A) = PR(B) / 2 + PR(C) + PR(D)/ 3
换句话说,根据链出总数平分一个页面的PR值
PR(A) = PR(B) / L(B) + PR(C) / L(C) + PR(D) / L(D)
为了防止没有外链的页面传递出去的PR是0,Google通过数学系统给每个页面分配一个很小的值(1-d)/N,以来表示该页面没有外链或者用户停止浏览直接jump
说明:
在Sergey Brin和Lawrence Page的1998年原文中给每一个页面设定的最小值是1-d,而不是这里的(1-d)/N(关于这一部分内容也可以参考英文版的维基百科词条)。 所以一个页面的PageRank是由其他页面的PageRank计算得到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值(非0),那么经过不断的重复计算,这些页面的PR值会趋向于稳定,也就是收敛的状态。
通过上述描述,简单总结PageRank的公式如下:

说明:处理那些“没有向外链接的页面”(这些页面就像“黑洞”会吞噬掉用户继续向下浏览的概率)带来的问题,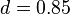 (这里的
(这里的 被称为阻尼系数(damping factor),其意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率。
被称为阻尼系数(damping factor),其意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率。 (就是用户停止点击,随机跳到新URL的概率)的算法被用到了所有页面上,估算页面可能被上网者放入书签的概率
(就是用户停止点击,随机跳到新URL的概率)的算法被用到了所有页面上,估算页面可能被上网者放入书签的概率
 是被研究的页面,
是被研究的页面,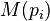 是链入
是链入 页面的集合,
页面的集合, 是
是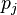 链出页面的数量,而
链出页面的数量,而 是所有页面的数量。
是所有页面的数量。
PageRank值是一个特殊矩阵中的特征向量。这个特征向量为

R是等式的答案
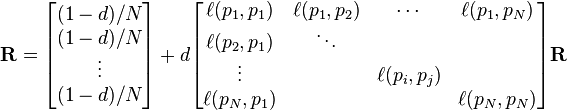
如果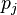 不链向
不链向 ,而且对每个
,而且对每个 都成立时,
都成立时,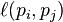 等于0
等于0
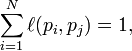
6、模拟html页面的关系,Java实现PageRank算法:
1 package com.pachira.d;
2
3 public class PageRank {
4 public static void main(String[] args) {
5 double[][] G = {
6 { 0, 1, 1/2.0, 0, 1/4.0, 1/2.0, 0},
7 {1/5.0, 0, 1/2.0, 1/3.0, 0, 0, 0},
8 {1/5.0, 0, 0, 1/3.0, 1/4.0, 0, 0},
9 {1/5.0, 0, 0, 0, 1/4.0, 0, 0},
10 {1/5.0, 0, 0, 1/3.0, 0, 1/2.0, 1},
11 { 0, 0, 0, 0, 1/4.0, 0, 0},
12 {1/5.0, 0, 0, 0, 0, 0, 0}
13 };
14 double[] PR = {1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0};
15 double alpha = 0.85;
16 double eps = 0.0000001;
17 pageRank(PR, G, alpha, eps);
18 }
19 public static void showVector(double[] v){
20 for (int i = 0; i < v.length; i++) {
21 System.out.print(v[i] + "\t");
22 }
23 System.out.println();
24 }
25 public static void showMatrix(double[][] m){
26 for (int i = 0; i < m.length; i++) {
27 for (int j = 0; j < m[i].length; j++) {
28 System.out.print(m[i][j] + "\t");
29 }
30 System.out.println();
31 }
32 }
33
34 /**
35 * 计算PageRank的主函数
36 * @param vector 初始的PageRank向量
37 * @param matrix 初始的HTML反向链接概率矩阵
38 * @param alpha 阻尼因子
39 * @param eps 收敛阈值
40 * @return
41 */
42 public static double[] pageRank(double[] vector, double[][] matrix, double alpha, double eps) {
43 double[] vectorMove = vector;
44 while (true) {
45 showVector(vector);
46 vectorMove = vectorXmatrix(vector, matrix, alpha);
47 double dis = norm(vector, vectorMove);
48 if (dis <= eps) {
49 break;
50 }
51 vector = vectorMove;
52 }
53 return vector;
54 }
55
56 /**
57 * 计算两个向量的误差
58 * @param vector
59 * @param vectorMove
60 * @return 向量的误差
61 */
62 public static double norm(double[] vector, double[] vectorMove) {
63 if (vector.length != vectorMove.length) {
64 return -1;
65 }
66 double sum = 0;
67 for (int i = 0; i < vector.length; i++) {
68 sum += Math.abs(vector[i] - vectorMove[i]);
69 }
70 return sum;
71 }
72
73 /**
74 * 计算PageRank值
75 * @param matrix HTML反向链接概率
76 * @param vector PageRank向量
77 * @return 新的PageRank向量
78 * @url: http://zh.wikipedia.org/zh/%E7%9F%A9%E9%98%B5
79 * 两个矩阵的乘法仅当第一个矩陣A的列數和另一个矩阵B的行數相等时才能定义。
80 * 如A是m×n矩陣和B是n×p矩陣,它們的乘積AB是一個m×p矩陣,它的一个元素
81 * | 1 0 2| |3 1| |(1*3 + 0*2 + 2*1) (1*1 + 0*1 + 2*0) | |5 1|
82 * |-1 3 1| x |2 1| = |(-1*3 + 3*2 + 1*1) (-1*1 + 3*1 + 1*0) | = |4 2|
83 * |1 0|
84 * | 1 0 2| | 1 | | 1*1 + 0*1 + 2*1| | 3 |
85 * |-1 3 1| x | 1 | = |-1*1 + 3*1 + 1*1| = | 3 |
86 * | 1 |
87 * |3 1|
88 * | 1 1 1| x |2 1| = |(1*3 + 1*2 + 1*1) (1*1 + 1*1 + 1*0)| = |6 2|
89 * |1 0|
90 */
91 public static double[] vectorXmatrix(double[] vector, double[][] matrix, double alpha) {
92 if(null == vector || matrix == null || vector.length == 0 || matrix.length == 0 || vector.length != matrix[0].length){
93 return null;
94 }
95 double[] result = new double[vector.length];
96 for (int i = 0; i < matrix.length; i++) {
97 double sum = 0;
98 for (int j = 0; j < matrix[i].length; j++) {
99 sum += vector[j] * matrix[i][j];
100 }
101 sum = alpha * sum + (1 - alpha) / vector.length;
102 result[i] = sum;
103 }
104 return result;
105 }
106 }
以上内容多摘自wiki的PageRank;





















 838
838

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








