[bzoj1016][JSOI2008]最小生成树计数 (Kruskal + Matrix Tree 定理)

Description

现在给出了一个简单无向加权图。你不满足于求出这个图的最小生成树，而希望知道这个图中有多少个不同的最小生成树。（如果两颗最小生成树中至少有一条边不同，则这两个最小生成树就是不同的）。由于不同的最小生成树可能很多，所以你只需要输出方案数对31011的模就可以了。

Input

第 一行包含两个数，n和m，其中1<=n<=100; 1<=m<=1000; 表示该无向图的节点数和边数。每个节点用1~n的整数编号。接下来的m行，每行包含两个整数：a, b, c，表示节点a, b之间的边的权值为c，其中1<=c<=1,000,000,000。数据保证不会出现自回边和重边。注意：具有相同权值的边不会超过10 条。

Output

输出不同的最小生成树有多少个。你只需要输出数量对31011的模就可以了。

Sample Input

4 6
1 2 1
1 3 1
1 4 1
2 3 2
2 4 1
3 4 1

Sample Output

8

分析

     先回忆一下求解最小生成树的过程：将边排序，贪心添加进当前生成森林中。由Kruskal算法的性质:【传送门】 ，在算法开始处理权值为val的边前，原图会形成若干个连通块，如图所示：

 图中的虚线表示原图中所有权值为val的边。通过与Kruskal算法相似的证明，我们可以知道在处理完边数为val的边后，形成的连通分量是一定的。也就是说，在这一过程中不论我们采取怎样的顺序，图中的点集S1,S2,S3一定连通，且这个新的连通块恰好是新的点集的一个最小生成树。

     那么，我们如何计算出这一过程可以有多少种连接方式呢？我们先把三个连通块都缩成点：

 

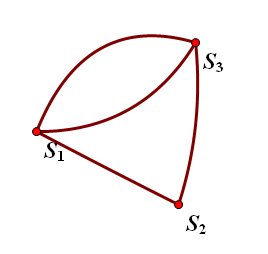
    我们的问题就变成了：在图中选取若干条边使得S1,S2,S3构成一棵树有多少种方案？这就转化为了一个数学问题：一般生成树计数，可以用Matrix-Tree定理来计算。

    于是我们就得到了本题的解法：1、将所有边升序排列；2、循环处理每一种权值形成的集合；3、对于同一种权值，利用Matrix-Tree定理求出当前处理的所有边可以产生的那些连通块的连接方式总数，乘入答案；4、将当前边可以产生的连通块缩成点。具体实现细节请看代码中的注释：

 

  1  /* *************************************************************
  2      Problem: 1016
  3      User: AsmDef
  4      Language: C++
  5      Result: Accepted
  6      Time:0 ms
  7      Memory:1292 kb
  8  *************************************************************** */
  9  
 10 #include <cctype>
 11 #include <cstdio>
 12 #include <iostream>
 13 #include <cmath>
 14 #include <cstdlib>
 15 #include <algorithm>
 16 #include <assert.h>
 17  using  namespace std;
 18 template<typename T>inline  void getd(T &x){
 19      char c = getchar();  bool minus =  0;
 20      while(!isdigit(c) && c !=  ' - ')c = getchar();
 21      if(c ==  ' - ')minus =  1, c = getchar();
 22     x = c -  ' 0 ';
 23      while(isdigit(c = getchar()))x = x *  10 + c -  ' 0 ';
 24      if(minus)x = -x;
 25 }
 26  /* ======================================================== */
 27  const  int maxn =  103, maxm =  1003, mod =  31011;
 28 typedef pair< int, pair< int,  int> > Edge; // 权值相同的边会按二元组(u,v)排序
 29  Edge E[maxm];
 30  #define val first
 31  #define u second.first
 32  #define v second.second
 33  int N, M, Ans =  1, *Mat[ 22], sum;
 34  
 35 inline  void watch();
 36  
 37  struct UFS{
 38      int pre[maxn];
 39      void init( int x){ for( int i =  0;i <= x;++i)pre[i] = i;}
 40      int find( int x){ return pre[x] == x ? x : pre[x] = find(pre[x]);}
 41      void link( int a,  int b){pre[find(a)] = find(b);}
 42 }ufs, tmpS; // ufs用于Kruskal,tmpS在计算Kirchhoff矩阵时判断当前所有边是否已经形成连通图
 43  inline  void init(){ // 读入原图
 44      getd(N), getd(M);
 45      int i;
 46     ufs.init(N);
 47      for(i =  0;i < M;++i)
 48         getd(E[i].u), getd(E[i].v), getd(E[i].val);
 49      for(i =  0;i <  21;++i)
 50         Mat[i] =  new  int[ 22]; // 使用动态内存，在det中简化“交换两行”的操作
 51      sort(E, E + M);
 52     sum = N;
 53 }
 54  
 55 inline  int det( int n){ // 计算N*N的Mat矩阵的行列式
 56       int i, j, k, t, ans =  1;
 57      for(i =  1;i < n;++i){
 58          for(j = i +  1;j < n;++j){
 59              while(Mat[j][i]){
 60                 t = Mat[i][i] / Mat[j][i];
 61                  if(t)
 62                      for(k = i;k < n;++k)
 63                         Mat[i][k] = (Mat[i][k] - Mat[j][k] * t) % mod;
 64                  
 65                 swap(Mat[i], Mat[j]), ans = -ans; // 交换两行时直接交换两行的内存指针即可
 66              }
 67         }
 68         ans = ans * Mat[i][i] % mod;
 69     }
 70      return ans;
 71 }
 72  int tmp[ 22], block[ 22], cnt;
 73 inline  void watch(){ // 调试用
 74       /* int i, j;
 75      for(i = 0;i < cnt;++i){
 76          for(j = 0;j < cnt;++j)
 77              printf("%5d ", Mat[i][j]);
 78          printf("\n\n");
 79      }
 80      printf("\n\n\n"); */
 81 }
 82  #define index(x) ( lower_bound(block, block + cnt, x) - block ) // 离散化后将点x映射到它所属的连通块编号
 83 
 84 inline  void calc(Edge *A,  int len){ // A[0]到A[len-1]之间的边权值相等，只需计算所有连接方法数即可
 85       int i, j;
 86      // int t, adj[22];
 87      cnt =  1;
 88      for(i =  0,j =  0;i < len;++i){
 89         A[i].u = ufs.find(A[i].u);
 90         A[i].v = ufs.find(A[i].v);
 91          if(A[i].u == A[i].v) continue;
 92         tmp[j++] = A[i].u;
 93         tmp[j++] = A[i].v;
 94     }
 95     sort(tmp, tmp + j); // 将出现的端点离散化
 96      block[ 0] = tmp[ 0];
 97      for(i =  1;i < j;++i)
 98          if(tmp[i] != block[cnt- 1])block[cnt++] = tmp[i]; // 去重后将新的连通块标号
 99       
100      for(i =  0;i < cnt;++i) for(j =  0;j < cnt;++j)
101         Mat[i][j] =  0;
102      
103     tmpS.init(cnt);
104      
105      for(i =  0;i < len;++i){
106          if(A[i].u == A[i].v) continue;
107          if(ufs.find(A[i].u) != ufs.find(A[i].v))--sum; // 原图中块数减少
108          ufs.link(A[i].u, A[i].v);
109         A[i].u = index(A[i].u);
110         A[i].v = index(A[i].v); // 构造缩点后的图
111          ++Mat[A[i].u][A[i].u];
112         ++Mat[A[i].v][A[i].v];
113          // adj[A[i].u] |= (1 << A[i].v);
114           // adj[A[i].v] |= (1 << A[i].u); // 理解错了Matrix-Tree定理，以为重边只算一次= =囧……
115          --Mat[A[i].u][A[i].v];
116         --Mat[A[i].v][A[i].u];
117         tmpS.link(A[i].u, A[i].v);
118     }
119      // 注意此时整个与当前边相关的图不一定连通，考虑完当前边后原图可能仍是一个森林，为了得到正确答案，我们可以在1以后每个新的连通块与之前的某个连通块之间加一条边。由于加入的每条边都是新图中的桥，这一操作并不会增加整张图的连接方法数。
120       int a, b;
121      for(i =  1;i < cnt;++i)
122          if((a = tmpS.find(i)) != (b = tmpS.find(i- 1))){
123             ++Mat[a][a], ++Mat[b][b];
124              // adj[a] |= (1 << b);adj[b] |= (1 << a);
125              --Mat[a][b], --Mat[b][a];
126             tmpS.link(a, b);
127         }
128      
129     Ans = Ans * det(cnt) % mod;
130 }
131 inline  void work(){
132      int i =  0, j =  1, t;
133      while(i < M){
134          while(j < M && E[i].val == E[j].val)++j; // 得到一段权值相等的边
135           if((t = j - i) >  1)calc(E + i, j - i);
136          else  if(ufs.find(E[i].u) != ufs.find(E[i].v)) // 当前权值唯一。直接缩点即可
137              ufs.link(E[i].u, E[i].v), --sum;
138         i = j++;
139     }
140      if(sum >  1)printf( " 0\n "); // 最终的图不连通
141       else
142         printf( " %d\n ", Ans);
143 }
144  int main(){
145      #if defined DEBUG
146     freopen( " test ",  " r ", stdin);
147      #else
148     #ifndef ONLINE_JUDGE
149     freopen( " bzoj_1016.in ",  " r ", stdin);
150     freopen( " bzoj_1016.out ",  " w ", stdout);
151      #endif
152      #endif
153     init();
154     work();
155      
156      return  0;
157 }

Kruskal + Matrix Tree定理

 

转载于:https://www.cnblogs.com/Asm-Definer/p/4372517.html