(1)如何理解核函数能把低维映射到高维
关键:因为有泰勒展开
严格说是为什么高斯核函数能够将低维映射到无穷维
对于高斯核为什么可以将数据映射到无穷多维,我们可以从泰勒展开式的角度来解释,
首先我们要清楚,SVM中,对于维度的计算,我们可以用内积的形式,假设函数: 表示一个简单的从二维映射到三维。
表示一个简单的从二维映射到三维。
则在SVM的计算中,可以表示为:
再来看 泰勒展开式:
泰勒展开式:
所以这个无穷多项的式子正是对于 的近似,
的近似, 所对应的映射:
所对应的映射:
再来看高斯核:

那么,对于
 和
和
 的内积形式符合在SVM中无穷维度下的内积计算,即高斯核将数据映射到无穷高的维度。
的内积形式符合在SVM中无穷维度下的内积计算,即高斯核将数据映射到无穷高的维度。
(2)为什么更倾向于选高斯核饿函数,而不是多项式核?
结论:多项式核函数可以将原始维度映射到高维,高斯核函数可以将原始维度映射到无穷维
比如


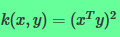
则有:
 =
=

找到特征映射
 因为
因为

- 则
 将
将  的点映射到
的点映射到 
2.现在分析高斯核



则有


根据泰勒公式

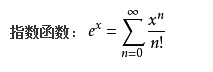
 那么
那么



可以看出公式中的的泰勒展开式其实是0-n维的多项式核函数的和。
我们知道多项式核函数将低维数据映射到高维(维度是有限的),那么 对于无限个 不同维的多项式核函数之和 的高斯核,其中也包括 无穷维度 的 多项式核函数。而且我们也找得到
 使
使
该等式

成立
而且维度 是无穷维。
资料
Why does the RBF (radial basis function) kernel map into infinite dimensional space?
核函数是一种特殊的 多项式核。
(3)几个概念
1)引入kernel的目的不是为了升维,而是升维后的简化计算。
Kernel Function只是一个关于特征向量的函数,本质是变换后的空间中的内积,这个函数的构造和引入的初衷只是为了提高SVM在高维的计算效率。
2)kernel和SVM是两回事,只是刚好在SVM中引入了kernel而已,这不是绑定的。kernel的出现要远远早于SVM,应用范围也远不止SVM
3)并不是所有情况下的kernel都要求满足Mercer条件(任何核矩阵为半正定的函数都可以作为核函数),SVM和GP(高斯过程)要求满足,但L1VM、L2VM、RVM都不要求kernel必须满足Mercer条件
4)Kernel是描述点和点之间关系的,或者说是距离。从距离空间出发,我们可以一步步往前走可以得到赋范向量空间,内积空间,然后是优美的希尔伯特空间。希尔伯特空间里面有好多概念,主要就是一个范数,一个内积。那什么是范数呢,范数就是我们之前强调的距离,或者说广义的距离。而什么又是内积呢?没错,内积就是这个距离的定义的方式。这就是为什么说由内积可以诱导出范数的原因了。既然kernel是用来描述点与点之间的关系或者说距离的话,那么一种可行的有效的方法就是用内积去刻画。
5)距离、内积(核函数)、相似度这三个词是等价的。(核函数会对应Gram矩阵)
5)SVM PCA 中都会用到核函数。SVM中的核函数是升维,PCA中的核函数是先升维,再朝某个方向投影,从而把不可分数据分开
6)Kernel 是隐式地将两个向量转换到其他形式然后求内积, 相比显式的转换可以极大的减少计算复杂度, 甚至可以将有限维的 x 转换到无限维. 与其先求出 再计算
再计算 , 不如直接算
, 不如直接算 , 这就是 kernel相对于手动(显式)转化的优势。
, 这就是 kernel相对于手动(显式)转化的优势。
7)
 :
:
核函数是二元函数,输入是变换之前的两个向量,其输出与两个向量变换之后的内积相等(这个性质非常重要)
使用核技巧之后,学习是隐式地在特征空间进行的,不需要显式地定义特征空间和映射函数(李航)
如何理解在二维空间内线性不可分的数据,在五维空间线性可分
链接 有几个图
f(x,y)=2x+3y是线性的,
f(x,y)=2x+3y+4xy是非线性的,
f(x,y,xy)=2x+3y+4xy是线性的.
SVM在线性不可分的的情况下 升维以后一定线性可分吗
升维后不一定线性可分,不过一般情况下升维后会更接近线性可分,这就够了。
通俗的说就是:投射到的维度越高,变为线性的可能性就越大。
像高斯核的话,就是投射到无穷维了,几乎所有问题都能解决。
(4)具体计算
1)引入kernel的目的不是为了升维,而是升维后的简化计算。
具体如下:我们要进行高维空间的线性可分,首先要将原始空间的点通过函数映射到特征空间中,然后学习,而所谓的学习,其实就是要计算高维空间的点的距离和夹角。那么能不能不通过映射函数而直接使用核函数计算高维空间的点的距离以及夹角呢? 答案是可以的,核函数的技巧就是不显示的定义映射函数,而在高维空间中直接使用核函数进行计算。

2)核函数的要求
首先介绍kernel矩阵,如下图所示:

核矩阵,就是每个点之间的高维映射之后的内积构成的矩阵。
要称为核函数,核矩阵必须是半正定的。
常用的核函数有:

在实际计算中,通常会选用高斯核。
核函数带来的好处很明显,如果先要映射到高维空间然后进行模型学习,计算量远远大于在低维空间中直接直接采用核函数计算
但是也有缺点,如果 φ(x) 具有足够高的维数,我们总是有足够的能力来拟合训练集,但是对于测试集的泛化往往不佳。非常通用的特征映射通常只基于局部光滑的原则,并且没有将足够的先验信息进行编码来解决高级问题
局部光滑原则,应该是区分传统机器学习和深度学习的重要特性。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








