最大流
感觉类似于匹配、分配,传递。
考虑每个流的实际意义和象征。
Poj 1149 PIGS(决策的流动与传递)
为了保证顺序,可以建n列m排点,每个人连ki到T,猪圈连在一起,依次决策。
点数nm。
其实可以更好。
发现其实很多点都是不变的,这样很浪费。
考虑分配的原因,本质是为了后面的人的选择。
所以,
源点到每个猪圈来买的第一个人连一条容量为该猪圈里猪的数量的边
对于每个猪圈,第i个来买的人向第i+1个来买的人连一条容量为正无穷的边
每个人向汇点连一条容量为购买数量的边
这样,每个人的面对的猪圈要么是没有动过的,要么是可能经过之前分配过的。符合题意。
人之间可以直接传递猪。就不用猪圈了。
点数n
注意n,m输入,先m后n。


#include<cstdio> #include<cstdlib> #include<algorithm> #include<cstring> #include<iostream> #define il inline #define reg register int #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=105; const int M=1005; const int inf=0x3f3f3f3f; int n,m; struct node{ int nxt,to; int w; }e[N*M*2+M*2]; int s,t; int hd[N],cnt=1; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=z; hd[x]=cnt; e[++cnt].nxt=hd[y]; e[cnt].to=x; e[cnt].w=0; hd[y]=cnt; } int pig[M],vis[M]; int las[M];//las has i 's ren int d[N+3]; int dfs(int x,int flow){ int res=flow; if(x==t) return flow; for(reg i=hd[x];i&&res;i=e[i].nxt){ int y=e[i].to; if(d[y]==d[x]+1&&e[i].w){ int k=dfs(y,min(res,e[i].w)); if(!k) d[y]=0; e[i].w-=k; e[i^1].w+=k; res-=k; } } return flow-res; } int q[N+3]; int l,r; bool bfs(){ l=1,r=0; memset(d,0,sizeof d); q[++r]=s; d[s]=1; while(l<=r){ int x=q[l++]; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(e[i].w&&!d[y]){ d[y]=d[x]+1; q[++r]=y; if(y==t) return true; } } } return false; } int main(){ rd(m);rd(n); for(reg i=1;i<=m;++i) rd(pig[i]); int x,c; s=0,t=n+1; for(reg i=1;i<=n;++i){ rd(c); while(c--){ rd(x); if(!las[x]) add(s,i,pig[x]),las[x]=i; else add(las[x],i,inf),las[x]=i; } rd(c); add(i,t,c); } int flow=0; int ans=0; while(bfs()){ while(flow=dfs(s,inf)) ans+=flow; } printf("%d",ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/14 7:58:25 */
POJ-1637 混合图欧拉回路(网络流的自我调节与反悔)
(题目保证图联通)
每个无向边只能经过一次,所以相当于给无向边定向。
一个有向图存在欧拉回路的条件是什么?
每个点的入度等于出度
给无向边随便定向,可能某些点的入度大于出度,某些点的出度大于入度
所有入度>出度的点从超级源点连一条容量为(入度-出度)/2的边,所有出度>入度的点向超级汇点连一条容量为(出度-入度)/2的边,然后对于原图中所有的定向为(a,b)无向边连一条从b到a容量为1的边
如果有点的入度与出度的差不是偶数,那么无解
满流有解
这样,每个流流经的边就代表要反向,为了保证最大流,其实每一股流都是S-x-y-T的。x-y的边就反向了。两个点的入度出度的差各自减少了2,和(出度-入度)/2是符合的。
易证,S连出去的流量等于连到T的流量。
所以如果满流,那么意味着经过一些边的反向处理,使得每个点入度与出度的差都抹平了。
(之后的上下界可行流也是这个思想)


#include<cstdio> #include<cstdlib> #include<algorithm> #include<cstring> #include<iostream> #define il inline #define reg register int #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=205; const int M=1005; const int inf=0x3f3f3f3f; int n,m; struct node{ int nxt,to; int w; }e[2*M+2*N+N+M]; int s,t; int hd[N],cnt=1; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=z; hd[x]=cnt; e[++cnt].nxt=hd[y]; e[cnt].to=x; e[cnt].w=0; hd[y]=cnt; } int d[N+3]; int dfs(int x,int flow){ int res=flow; if(x==t) return flow; for(reg i=hd[x];i&&res;i=e[i].nxt){ int y=e[i].to; if(d[y]==d[x]+1&&e[i].w){ int k=dfs(y,min(res,e[i].w)); if(!k) d[y]=0; e[i].w-=k; e[i^1].w+=k; res-=k; } } return flow-res; } int q[N+3]; int l,r; int du[N]; bool bfs(){ l=1,r=0; memset(d,0,sizeof d); q[++r]=s; d[s]=1; while(l<=r){ int x=q[l++]; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(e[i].w&&!d[y]){ d[y]=d[x]+1; q[++r]=y; if(y==t) return true; } } } return false; } void clear(){ memset(hd,0,sizeof hd); cnt=1; memset(du,0,sizeof du); } int main(){ int T; rd(T); while(T--){ clear(); rd(n);rd(m); int x,y,z; for(reg i=1;i<=m;++i){ rd(x);rd(y);rd(z); du[y]++; du[x]--; if(!z){ add(y,x,1); } } s=0,t=n+1; bool fl=true; int tot=0; for(reg i=1;i<=n;++i){ if(du[i]%2){ fl=false;break; } if(du[i]<0){ add(i,t,(-du[i])/2); }else{ add(s,i,du[i]/2); tot+=du[i]/2; } } if(!fl){ printf("impossible\n");continue; } int flow=0; int maxflow=0; while(bfs()){ while(flow=dfs(s,inf)) maxflow+=flow; } if(maxflow==tot){ printf("possible\n"); }else{ printf("impossible\n"); } } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/14 9:03:26 */
匹配问题
侧重于一些人,一些物品,进行分配,求全局最优收益
通常考虑能不能变成二分图,或者类二分图(明显的左右部分几列点),找到这样的性质的话,
由于二分图内部不用考虑连边,通常就比较好做了。
[USACO07OPEN]吃饭Dining(拆点限制贡献)
比较基础的匹配题。
题目条件是:
1.饮料、食物只有一个,可以考虑左边放食物,右边饮料,然后S-食物,饮料-T ,容量为1来限制
2.一头牛喜欢若干个。把牛放中间,两边对饮料食物连边
3.一头牛只会吃一个饮料食物,贡献1的代价。如果象上面那样直接做的话, 可能一个牛吃了很多份,贡献了很多的贡献
所以考虑把牛拆点,中间连容量为1的边,这样的话,保证了每个牛只会吃一份食物。贡献1的代价
跑最大流即可
一条流的意义是,一个牛选择了一种饮料和食物,贡献1的贡献。最后的最大流一定是合法的。
EZOJ某题:宝石迷阵
棋盘问题。考虑能不能二分图。
一般的传统黑白染色不能很好的处理L形、每个能量石贡献1次、每个水晶贡献一次
那就观察性质:
L形是什么?
点的上下选择一个,左右选择一个
如果我们把奇数列作为左部点,偶数列作为右部点,那么每个水晶一定从左部点拿一个,右部点拿一个。然后贡献1的贡献
这样的二分图性质,使得奇数、偶数列自己之间不会有边,就好想了很多。
把水晶拆点,相邻的能量石连边,就类似上面一个题了。


#include<cstdio> #include<cstdlib> #include<algorithm> #include<cstring> #include<iostream> #define il inline #define reg register int #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=2500; const int M=1005; const int inf=0x3f3f3f3f; int n,m; struct node{ int nxt,to; int w; }e[(N+N*2*2+N*2)*2]; int s,t; int hd[4*N],cnt=1; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=z; hd[x]=cnt; e[++cnt].nxt=hd[y]; e[cnt].to=x; e[cnt].w=0; hd[y]=cnt; } int d[4*N+3]; int dfs(int x,int flow){ int res=flow; if(x==t) return flow; for(reg i=hd[x];i&&res;i=e[i].nxt){ int y=e[i].to; if(d[y]==d[x]+1&&e[i].w){ int k=dfs(y,min(res,e[i].w)); if(!k) d[y]=0; e[i].w-=k; e[i^1].w+=k; res-=k; } } return flow-res; } int q[4*N+3]; int l,r; bool bfs(){ l=1,r=0; memset(d,0,sizeof d); q[++r]=s; d[s]=1; while(l<=r){ int x=q[l++]; //cout<<" xx "<<x<<endl; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(e[i].w&&!d[y]){ d[y]=d[x]+1; q[++r]=y; if(y==t) return true; } } } return false; } char mp[55][55]; int num(int x,int y){ return (x-1)*m+y; } int main(){ rd(n);rd(m); s=0,t=n*m+n*m+1; for(reg i=1;i<=n;++i){ scanf("%s",mp[i]+1); for(reg j=1;j<=m;++j){ if(mp[i][j]=='X') continue; if((i+j)%2==0){ if(j%2==1){ if(i>1) add(num(i-1,j),num(i,j),1); if(i<n) add(num(i+1,j),num(i,j),1); if(j>1) add(num(i,j)+n*m,num(i,j-1),1); if(j<m) add(num(i,j)+n*m,num(i,j+1),1); } else{ if(i>1) add(num(i,j)+n*m,num(i-1,j),1); if(i<n) add(num(i,j)+n*m,num(i+1,j),1); if(j>1) add(num(i,j-1),num(i,j),1); if(j<m) add(num(i,j+1),num(i,j),1); } add(num(i,j),num(i,j)+n*m,1); }else{ if(j%2==1){ add(s,num(i,j),1); }else{ add(num(i,j),t,1); } } } } int ans=0,flow=0; while(bfs()){ while(flow=dfs(s,inf)) ans+=flow; }cout<<ans; return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/14 10:17:33 */
费用流
一般的标志是,最大化。、。。的前提下,最小/最大化花费/收益
所以,建模的时候,不但要考虑到最小费用,更要考虑到是否能满足最大流的限制。
[SDOI2010]星际竞速
新建一个:[SDOI2010]星际竞速
「清华集训 2017」无限之环
比较强大的网络流综合题
[NOI2012]美食节+修车——费用流(带权二分图匹配)+动态加边
[WC2007]剪刀石头布
新建一篇:[WC2007]剪刀石头布——费用流
最小割
同时存在,一个存在一个不存在,一个存在一些必须存在的问题。
也就是,一些东西选择或者不选择产生的代价、利益、以至于合法性,都是可能会互相之间影响的。
可以考虑最小割。
割断代表选择,或者不选择。也通常通过∑-最小割 来处理最大化利益的问题
bzoj 3158 千钧一发
最小割也往往要考虑能否转化成二分图的形式。
这个题,最大化收益,还要两两之间可能还有限制。那么最小割跑不了
直接限制不好找到S,T的连边
两两之间限制有些特殊,能不能找到二分图的性质?
也就是,能不能根据ai的一些性质分成两类,使得每一类自己不会产生冲突?
发现,偶数之间,都满足条件2,不会有冲突
奇数之间,由于平方和是偶数,而且还是一个完全平方数,那么这个平方和还必须是4的倍数,但是(2a+1)^2+(2b+1)^2=4*(.....)+2,不是4的倍数!不会有冲突
所以,按照ai的奇偶,分成左右部点,冲突只会产生在左右部点之间
然后n^2枚举,看是否有冲突。然后连inf的边,左右部点向S或者T连bi的边。
每个割集都对应一个删除方案,使得留下的都是合法的。
跑最小割,
∑bi-最小割 就是ans
注意,ai*ai会爆int


#include<bits/stdc++.h> #define il inline #define reg register int #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1005; const int inf=0x3f3f3f3f; int n,m,s,t,k; struct node{ int nxt,to; int w; }e[2*(N+N*N+N)]; int hd[N],cnt=1; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=z; hd[x]=cnt; e[++cnt].nxt=hd[y]; e[cnt].to=x; e[cnt].w=0; hd[y]=cnt; } int d[N]; int dfs(int x,int flow){ int res=flow; if(x==t) return flow; for(reg i=hd[x];i&&res;i=e[i].nxt){ int y=e[i].to; if(e[i].w&&d[y]==d[x]+1){ int k=dfs(y,min(e[i].w,res)); if(!k) d[y]=0; res-=k; e[i].w-=k; e[i^1].w+=k; } } return flow-res; } int q[N],l,r; bool bfs(){ l=1,r=0; memset(d,0,sizeof d); d[s]=1; q[++r]=s; while(l<=r){ int x=q[l++]; //cout<<" bfs "<<x<<endl; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(!d[y]&&e[i].w){ d[y]=d[x]+1; q[++r]=y; if(y==t) return true; } } } return false; } int gcd(int a,int b){ return b?gcd(b,a%b):a; } int a[N],b[N]; int main(){ rd(n); s=0,t=n+1; for(reg i=1;i<=n;++i) { rd(a[i]); } int ans=0; for(reg i=1;i<=n;++i) rd(b[i]),ans+=b[i]; //cout<<" ans "<<ans<<endl; for(reg i=1;i<=n;++i){ if(a[i]%2){ add(s,i,b[i]); for(reg j=1;j<=n;++j){ if(a[j]%2==0){ int g=gcd(a[i],a[j]); if(g!=1) continue; ll lp=(ll)a[i]*a[i]+(ll)a[j]*a[j]; double kk=sqrt(lp); double ll=floor(kk); //cout<<" kk "<<kk<<" ll "<<ll<<endl; if(kk-ll<=0.000001){ //cout<<" add "<<a[i]<<" "<<a[j]<<endl; add(i,j,inf); } } } }else{ add(i,t,b[i]); } } int flow=0,maxflow=0; while(bfs()){ while(flow=dfs(s,inf)) maxflow+=flow; } ans-=maxflow; cout<<ans<<endl; return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/15 9:47:25 */
每竖条只能切一刀,并且相邻只能距离小于等于D
那么排出长*宽条纵向的,每条H个。边权是v[i][j][k]
考虑怎么限制D
一个边给相邻的四联通的四列如下连边
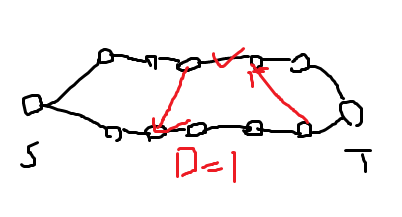
如果切了打钩的边,那么如果相邻的不切距离为D的那三条,那么一定还有走过红色的一条路径。
显然一行割两个不优,并且相邻距离不在D的范围内割也不优,所以一定合法。
最小割dp
边数太多而网络流图比较有规律(例如二分图等等)可以考虑用dp实现最小割
必要的时候之前的点和S或者T的连通性
由于最小割直观好操作,最大流也可以转化成最小割dp
二元关系
平面图最小割=对偶图最短路
建一个模建好了就一目了然了。S到T的路径和和有意义的割集就是一一对应的了。
还有一个不是那么显然的
发现,平着走和下降都是不耗费体力的。所以边权一定[0,1]之间
如果是小数的话,那么与其这样慢慢走,总流量一定不如直接选择最小的一层直接走1,别的平着走0,因为层数的高度会累加到1的。
所以,一定是一堆0,然后一堆1,
0,1自己都是联通块。
最小割转对偶图最短路即可。
边的输入比较麻烦,建图还要有双向的边的限制,考虑路径和割集的意义。只要路径边的正反方向边权不一样即可。


#include<bits/stdc++.h> #define il inline #define reg register int #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(ll &x){ char ch;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=505; const int V=500*500+5; const ll inf=0x3f3f3f3f3f3f3f3f; int n; struct node{ int nxt,to;ll w; }e[2*(V*4)+233]; int s,t; ll dis[V]; int hd[V]; int cnt; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y; e[cnt].w=z; hd[x]=cnt; } struct po{ int x;ll v; po(){} po(int xx,ll y){ x=xx,v=y; } bool friend operator <(po a,po b){ return a.v>b.v; } }; priority_queue<po>q; bool vis[V]; ll dij(){ q.push(po(s,0)); while(!q.empty()){ po now=q.top();q.pop(); if(vis[now.x]) continue; vis[now.x]=1,dis[now.x]=now.v; for(reg i=hd[now.x];i;i=e[i].nxt){ int y=e[i].to; if(!vis[y]){ q.push(po(y,now.v+e[i].w)); } } } return dis[t]; } int num(int i,int j){ return (i-1)*n+j; } int main(){ scanf("%d",&n); s=0,t=n*n+1; ll x; for(reg i=1;i<=n+1;++i){ for(reg j=1;j<=n;++j){ rd(x); if(i>1&&i<=n){ add(num(i-1,j),num(i,j),x); }else if(i==1){ add(s,num(i,j),x); }else if(i==n+1){ add(num(i-1,j),t,x); } } } for(reg i=1;i<=n;++i){ for(reg j=1;j<=n+1;++j){ rd(x); if(j>1&&j<=n){ add(num(i,j),num(i,j-1),x); }else if(j==1){ add(num(i,j),t,x); }else if(j==n+1){ add(s,num(i,j-1),x); } } } for(reg i=1;i<=n+1;++i){ for(reg j=1;j<=n;++j){ rd(x); if(i>1&&i<=n){ add(num(i,j),num(i-1,j),x); }else if(i==1){ add(num(i,j),s,x); }else if(i==n+1){ add(t,num(i-1,j),x); } } } for(reg i=1;i<=n;++i){ for(reg j=1;j<=n+1;++j){ rd(x); if(j>1&&j<=n){ add(num(i,j-1),num(i,j),x); }else if(j==1){ add(t,num(i,j),x); }else if(j==n+1){ add(num(i,j-1),s,x); } } } printf("%lld",dij()); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/16 21:22:32 */
最小割树
预处理,之后求任意两点最小割(最大流)
最大权闭合子图
DAG中(不是DAG可以缩点),处理一些选择A就必须选择B的限制。
上下界网络流
适用于一类边的容量有上下界的问题。
网络流是什么?
一类建模题,,,,
适用范围非常广。匹配,关联,限制,传递等基础下的一系列最优化问题。
复杂度玄学。总点数、边数的数据范围一般在100~10000之间,不太大也不太小。。。
难点在于:
1.看出这是一个网络流题。。。
考虑数据范围?
dp、贪心、其他图论建模等都不是?
2.建模
具体情况具体分析。
归纳为匹配,关联,限制,传递等问题,熟悉最大流、最小割、费用流、上下界网络流的擅长类别。
































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








