【codeup】1959: 全排列 及全排列算法详解

题目描述

给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。
我们假设对于小写字母有'a' < 'b' < ... < 'y' < 'z'，而且给定的字符串中的字母已经按照从小到大的顺序排列。

输入

输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。

输出

输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义：
已知S = s1s2...sk , T = t1t2...tk，则S < T 等价于，存在p (1 <= p <= k)，使得
s1 = t1, s2 = t2, ..., sp - 1 = tp - 1, sp < tp成立。

注意每组样例输出结束后接一个空行。

样例输入

xyz

样例输出

xyz
xzy
yxz
yzx
zxy
zyx

提示

 

用STL中的next_permutation会非常简洁。

 

 

思路：

由于题目提示使用next_permutation会简洁，所以这里我们使用此方法。

 1 #include<iostream>
 2 #include<stdio.h>
 3 #include<queue>
 4 #include<string>
 5 #include<string.h>
 6 #include<algorithm>
 7 using namespace std;
 8 
 9 char a[10];
10 
11 int main()
12 {
13     int n;
14     while(scanf("%s",a)!=EOF)
15     {
16         n=strlen(a);
17         do
18         {
19             printf("%s\n",a);
20         }while(next_permutation(a,a+n));
21         puts("");
22     }
23     return 0;
24 }

C++/STL中定义的next_permutation和prev_permutation函数是非常灵活且高效的一种方法，它被广泛的应用于为指定序列生成不同的排列。

next_permutation函数将按字母表顺序生成给定序列的下一个较大的排列，直到整个序列为降序为止。

prev_permutation函数与之相反，是生成给定序列的上一个较小的排列。

所谓“下一个”和“上一个”，举一个简单的例子：

　　对序列 {a, b, c}，每一个元素都比后面的小，按照字典序列，固定a之后，a比bc都小，c比b大，它的下一个序列即为{a, c, b}，而{a, c, b}的上一个序列即为{a, b, c}，同理可以推出所有的六个序列为：{a, b, c}、{a, c, b}、{b, a, c}、{b, c, a}、{c, a, b}、{c, b, a}，其中{a, b, c}没有上一个元素，{c, b, a}没有下一个元素。

二者原理相同，仅遍例顺序相反，这里仅以next_permutation为例介绍算法。

(1) int 类型的next_permutation

int main()
{
    int a[3];
    a[0]=1;a[1]=2;a[2]=3;
    do
    {
        cout<<a[0]<<" "<<a[1]<<" "<<a[2]<<endl;
    }while (next_permutation(a,a+3)); //参数3指的是要进行排列的长度

//如果存在a之后的排列，就返回true。如果a是最后一个排列没有后继，返回false，每执行一次，a就变成它的后继
}

输出：
 1 2 3
 1 3 2
 2 1 3
 2 3 1
 3 1 2
 3 2 1

如果改成

 1 while(next_permutation(a,a+2)); 

则输出：
 1 2 3
 2 1 3
只对前两个元素进行字典排序

显然，如果改成

 1 while(next_permutation(a,a+1));  

则只输出：1 2 3
 
若排列本来就是最大的了没有后继，则next_permutation执行后，会对排列进行字典升序排序,相当于循环
 

1 int list[3]={3,2,1};
2 next_permutation(list,list+3);
3 cout<<list[0]<<" "<<list[1]<<" "<<list[2]<<endl;

输出: 1 2 3
 
(2) char 类型的next_permutation
 

int main()
{
    char ch[205];
    cin >> ch;
 
    sort(ch, ch + strlen(ch) );
    //该语句对输入的数组进行字典升序排序。如输入9874563102
    cout<<ch;//将输出0123456789,这样就能输出全排列了
 
    char *first = ch;
    char *last = ch + strlen(ch);
 
    do {
        cout<< ch << endl;
    }while(next_permutation(first, last));
     return 0;
}
 
//这样就不必事先知道ch的大小了，是把整个ch字符串全都进行排序
//若采用 while(next_permutation(ch,ch+5)); 如果只输入1562，就会产生错误，因为ch中第五个元素指向未知
//若要整个字符串进行排序，参数5指的是数组的长度，不含结束符

(3) string 类型的next_permutation
 

int main()
{
    string line;
    while(cin>>line&&line!="#")
    {
        if(next_permutation(line.begin(),line.end())) //从当前输入位置开始
        cout<<line<<endl;
        else cout<<"Nosuccesor\n";
    }
}

int main()
{
    string line;
    while(cin>>line&&line!="#")
    {
        sort(line.begin(),line.end());//全排列
        cout<<line<<endl;
        while(next_permutation(line.begin(),line.end()))
        cout<<line<<endl;
    }
}

 

 next_permutation 自定义比较函数
 

#include<iostream> //poj 1256 Anagram
#include<cstring>
#include<algorithm>
using namespace std;
int cmp(char a,char b) //'A'<'a'<'B'<'b'<...<'Z'<'z'.
{
    if(tolower(a)!=tolower(b))
        return tolower(a)<tolower(b);
    else
        return a<b;
}
int main()
{
    char ch[20];
    int n;
    cin>>n;
    while(n--)
    {
        scanf("%s",ch);
        sort(ch,ch+strlen(ch),cmp);
        do
        {
            printf("%s\n",ch);
        }while(next_permutation(ch,ch+strlen(ch),cmp));
    }
    return 0;
}

 

用next_permutation和prev_permutation求排列组合很方便，但是要记得包含头文件#include <algorithm>。

虽然最后一个排列没有下一个排列，用next_permutation会返回false，但是使用了这个方法后，序列会变成字典序列的第一个，如cba变成abc。prev_permutation同理。

 

 

 

 

 

全排列生成算法

对于给定的集合A{a1,a2,...,an},其中的n个元素互不相同，如何输出这n个元素的所有排列（全排列）。

递归算法

这里以A{a,b,c}为例，来说明全排列的生成方法，对于这个集合，其包含3个元素，所有的排列情况有3!=6种，对于每一种排列，其第一个元素有3种选择a,b,c，对于第一个元素为a的排列，其第二个元素有2种选择b,c；第一个元素为b的排列，第二个元素也有2种选择a，c，……，依次类推，我们可以将集合的全排列与一棵多叉树对应。如下图所示

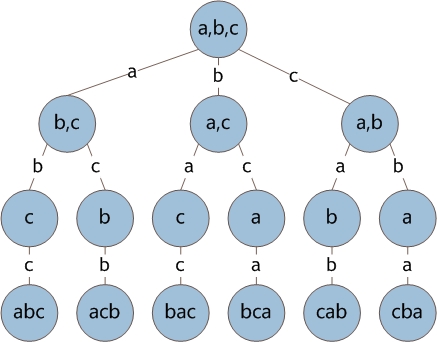
在此树中，每一个从树根到叶子节点的路径，就对应了集合A的一个排列。通过递归算法，可以避免多叉树的构建过程，直接生成集合A的全排列，代码如下。

 

 1 template <typename T>
 2 inline void swap(T* array, unsigned int i, unsigned int j)
 3 {
 4     T t = array[i];
 5     array[i] = array[j];
 6     array[j] = t;
 7 }
 8 
 9 /*
10  * 递归输出序列的全排列
11  */
12 void FullArray(char* array, size_t array_size, unsigned int index)
13 {
14     if(index >= array_size)
15     {
16         for(unsigned int i = 0; i < array_size; ++i)
17         {
18             cout << array[i] << ' ';
19         }
20 
21         cout << '\n';
22 
23         return;
24     }
25 
26     for(unsigned int i = index; i < array_size; ++i)
27     {
28         swap(array, i, index);
29 
30         FullArray1(array, array_size, index + 1);
31 
32         swap(array, i, index);
33     }
34 }

 

 

该算法使用原始的集合数组array作为参数代码的28～32行，将i位置的元素，与index位置的元素交换的目的是使得array[index + 1]到array[n]的所有元素，对应当前节点的后继结点，递归调用全排列生成函数。调用结束之后还需要回溯将交换位置的元素还原，以供其他下降路径使用。

字典序

全排列生成算法的一个重要思路，就是将集合A中的元素的排列，与某种顺序建立一一映射的关系，按照这种顺序，将集合的所有排列全部输出。这种顺序需要保证，既可以输出全部的排列，又不能重复输出某种排列，或者循环输出一部分排列。字典序就是用此种思想输出全排列的一种方式。这里以A{1,2,3,4}来说明用字典序输出全排列的方法。

首先，对于集合A的某种排列所形成的序列，字典序是比较序列大小的一种方式。以A{1,2,3,4}为例，其所形成的排列1234<1243，比较的方法是从前到后依次比较两个序列的对应元素，如果当前位置对应元素相同，则继续比较下一个位置，直到第一个元素不同的位置为止，元素值大的元素在字典序中就大于元素值小的元素。上面的a1[1...4]=1234和a2[1...4]=1243，对于i=1,i=2，两序列的对应元素相等，但是当i=2时，有a1[2]=3<a2[2]=4，所以1234<1243。

使用字典序输出全排列的思路是，首先输出字典序最小的排列，然后输出字典序次小的排列，……，最后输出字典序最大的排列。这里就涉及到一个问题，对于一个已知排列，如何求出其字典序中的下一个排列。这里给出算法。

• 对于排列a[1...n]，找到所有满足a[k]<a[k+1](0<k<n-1)的k的最大值，如果这样的k不存在，则说明当前排列已经是a的所有排列中字典序最大者，所有排列输出完毕。
• 在a[k+1...n]中，寻找满足这样条件的元素l，使得在所有a[l]>a[k]的元素中，a[l]取得最小值。也就是说a[l]>a[k]，但是小于所有其他大于a[k]的元素。
• 交换a[l]与a[k].
• 对于a[k+1...n]，反转该区间内元素的顺序。也就是说a[k+1]与a[n]交换，a[k+2]与a[n-1]交换，……，这样就得到了a[1...n]在字典序中的下一个排列。

这里我们以排列a[1...8]=13876542为例，来解释一下上述算法。首先我们发现，1(38)76542，括号位置是第一处满足a[k]<a[k+1]的位置，此时k=2。所以我们在a[3...8]的区间内寻找比a[2]=3大的最小元素，找到a[7]=4满足条件，交换a[2]和a[7]得到新排列14876532，对于此排列的3～8区间，反转该区间的元素，将a[3]-a[8]，a[4]-a[7]，a[5]-a[6]分别交换，就得到了13876542字典序的下一个元素14235678。下面是该算法的实现代码

 

 1 /*
 2  * 将数组中的元素翻转
 3  */
 4 inline void Reverse(unsigned int* array, size_t array_size)
 5 {
 6     for(unsigned i = 0; 2 * i < array_size - 1; ++i)
 7     {
 8         unsigned int t = array[i];
 9         array[i] = array[array_size - 1 - i];
10         array[array_size - 1 - i] = t;
11     }
12 }
13 
14 inline int LexiNext(unsigned int* lexinum, size_t array_size)
15 {
16     unsigned int i, j, k, t;
17 
18     i = array_size - 2;
19 
20     while(i != UINT_MAX && lexinum[i] > lexinum[i + 1])
21     {
22         --i;
23     }
24 
25     //达到字典序最大值
26     if(i == UINT_MAX)
27     {
28         return 1;
29     }
30 
31     for(j = array_size - 1, k = UINT_MAX; j > i; --j)
32     {
33         if(lexinum[j] > lexinum[i])
34         {
35             if(k == UINT_MAX)
36             {
37                 k = j;
38             }
39             else
40             {
41                 if(lexinum[j] < lexinum[k])
42                 {
43                     k = j;
44                 }
45             }
46         }
47     }
48 
49     t = lexinum[i];
50     lexinum[i] = lexinum[k];
51     lexinum[k] = t;
52 
53     Reverse(lexinum + i + 1, array_size - i - 1);
54     return 0;
55 }
56 
57 /*
58  * 根据字典序输出排列
59  */
60 inline void ArrayPrint(const char* array, size_t array_size, const unsigned int* lexinum)
61 {
62     for(unsigned int i = 0; i < array_size; ++i)
63     {
64         cout << array[lexinum[i]] << ' ';
65     }
66 
67     cout << '\n';
68 }
69 
70 /*
71  * 基于逆序数的全排列输出
72  */
73 void FullArray(char* array, size_t array_size)
74 {
75     unsigned int lexinumber[array_size];
76 
77     for(unsigned int i = 0; i < array_size; ++i)
78     {
79         lexinumber[i] = i;
80     }
81 
82     ArrayPrint(array, array_size, lexinumber);
83 
84     while(!LexiNext(lexinumber, array_size))
85     {
86         ArrayPrint(array, array_size, lexinumber);
87     }
88 }

 

使用字典序输出集合的全排列需要注意，因为字典序涉及两个排列之间的比较，对于元素集合不方便比较的情况，可以将它们在数组中的索引作为元素，按照字典序生成索引的全排列，然后按照索引输出对应集合元素的排列，示例代码使用的就是此方法。对于集合A{a,b,c,d}，可以对其索引1234进行全排列生成。这么做还有一个好处，就是对于字典序全排列生成算法，需要从字典序最小的排列开始才能够生成集合的所有排列，如果原始集合A中的元素不是有序的情况，字典序法将无法得到所有的排列结果，需要对原集合排序之后再执行生成算法，生成索引的全排列，避免了对原始集合的排序操作。

字典序算法还有一个优点，就是不受重复元素的影响。例如1224，交换中间的两个2，实际上得到的还是同一个排列，而字典序则是严格按照排列元素的大小关系来生成的。对于包含重复元素的输入集合，需要先将相同的元素放在一起，以集合A{a,d,b,c,d,b}为例，如果直接对其索引123456进行全排列，将不会得到想要的结果，这里将重复的元素放到相邻的位置，不同元素之间不一定有序，得到排列A'{a,d,d,b,b,c}，然后将不同的元素，对应不同的索引值，生成索引排列122334，再执行全排列算法，即可得到最终结果。

 

 

Steinhaus-Johnson-Trotter算法是一种基于最小变换的全排列生成算法，对于排列a[1...n]，该算法通过将a[i]，与a[i-1]（或a[i+1]）进行交换，生成下一个排列，直到所有排列生成完毕为止，这样，当前排列与其后继排列只是两个相邻位置的元素发生了调换。当然，为了防止重复生成某一个排列，算法并非随意调换某两个元素之间的位置，其生成全排列的具体规则如下。

• 首先，以字典序最小的排列起始，并且为该排列的每个元素赋予一个移动方向，初始所有元素的移动方向都向左。
• 在排列中查找这样的元素，该元素按照其对应的移动方向移动，可以移动到一个合法位置，且移动方向的元素小于该元素，在所有满足条件的元素中，找到其中的最大者。
• 将该元素与其移动方向所对应的元素交换位置。
• 对于排列中，所有元素值大于该元素的元素，反转其移动方向。

这里有几个概念需要说明一下，所谓合法位置，是指该元素按照其移动方向移动，不会移动到排列数组之外，例如对于<4，<1，<2，<3，此时对于元素4，如果继续向左移动，就会超过数组范围，所以4的下一个移动位置是非法位置。而且，所有元素，都只能向比自己小的元素的方向移动，如上面例子中的元素2，3，而元素1是不能够移动到元素4的位置的。每次移动，都要对可以移动的所有元素中的最大者进行操作，上例中元素1，4不能移动，2，3都存在合法的移动方案，此时需要移动3，而不能移动2。合法移动之后，需要将所有大于移动元素的元素的移动方向反转，上例中的元素3移动后的结果是4>，1<，<3，<2，可以看到，元素4的移动方向改变了。再如此例子<2，<1，3>，4>，对于其中的元素2，4，其对应的下一个移动位置都是非法位置，而对于元素1，3，其下一个移动位置的元素，都比他们要大，对于该排列就找不到一个可以的移动方案，这说明该算法已经达到终态，全排列生成结束。下面是该算法的代码

 

 1 inline int SJTNext(unsigned int* index, size_t array_size, int* move)
 2 {
 3     unsigned int i, j, t;
 4 
 5     //找到最大合法移动的元素索引
 6     for(i = array_size - 1, j = array_size; i != UINT_MAX; --i)
 7     {
 8         if(i + move[i] < array_size && index[i] > index[i + move[i]])
 9         {
10             if(j == array_size)
11             {
12                 j = i;
13                 continue;
14             }
15 
16             if(index[i] > index[j])
17             {
18                 j = i;
19             }
20         }
21     }
22 
23     //未发现合法的移动策略
24     if(j == array_size)
25     {
26         return 1;
27     }
28 
29     t = index[j];//要交换位置的元素
30     i = j + move[j];//发生交换的位置
31     swap(index, i, j);
32     swap(move, i, j);
33 
34     //将所有比t大的元素的移动方向反转
35     for(i = 0; i < array_size; ++i)
36     {
37         if(index[i] > t)
38         {
39             move[i] = -move[i];
40         }
41     }
42 
43     return 0;
44 }
45 
46 /*
47  * 基于最小变换的Steinhaus–Johnson–Trotter算法
48  */
49 void FullArray(char* array, size_t array_size)
50 {
51     unsigned int index[array_size];
52     int move[array_size];
53 
54     for(unsigned int i = 0; i < array_size; ++i)
55     {
56         index[i] = i;
57         move[i] = -1;
58     }
59 
60     ArrayPrint(array, array_size, index);
61 
62     while(!SJTNext(index, array_size, move))
63     {
64         ArrayPrint(array, array_size, index);
65     }
66 }

 

代码使用了一个伴随数组move标记对应位置元素的移动方向，在元素移动时，move数组中的对应元素也要相应移动。该算法从初始排列<1,<2,<3,<4开始，可以生成4元素的所有排列，直至最终排列<2，<1，3>，4>为止，其状态转移如下图所示，该图片来自于Wiki百科。

实际上该算法是Shimon Even对于Steinhaus-Johnson-Trotter三人提出的全排列生成算法的改进算法，在算法中实际上还有一个问题需要解决，就是对于给定的排列，如何判断其所有元素的移动方向，如果上面所谓终态的移动方向是<2，<1，3>，<4，那么这个状态就还存在可行的移动方案。Johnson(1963)给出了判断当前排列各元素移动方向的方法，对于排列中的每个元素，判断所有比该元素小的元素所生成序列的逆序数，如果逆序数为偶，则该元素的移动方向为向左，否则移动方向向右，我们用这条原则来看一下上面的终态2，1，3，4。对于元素1，没有比1小的元素，此时我们认为，空序列的逆序数为偶，所以元素1的移动方向向左；对于元素2，比2小的元素形成的序列为1，单元素序列的逆序数为偶，所以2的移动方向向左；对于元素3，小于3的元素组成的序列为21，逆序数为1，奇数，所以3的移动方向向右；对于元素4，对应序列为213，逆序数为奇数，所以4的移动方向向右。根据该规则就可以知道，给定某一排列，其对应元素的移动方向是确定的。

 

 

基于阶乘数的全排列生成算法，是另一种通过序列顺序，输出全排列的算法。所谓阶乘数，实际上和我们常用的2进制，8进制，10进制，16进制一样，是一种数值的表示形式，所不同的是，上面这几种进制数，相邻位之间的进制是固定值，以10进制为例，第n位与第n+1位之间的进制是10，而阶乘数，相邻两位之间的进制是变值，第n位与第n+1位之间的进制是(n+1)!。对于10进制数，每一位的取值范围也是固定的0～9，而阶乘数每一位的取值范围为0～n。可以证明，任何一个数量，都可以由一个阶乘数唯一表示。下面以23为例，说明其在各种进制中的表现形式

	2进制	8进制	10进制	16进制	阶乘数
23	10111	27	23	17	3210

 

其中10进制23所代表的数量的计算方法为

D(23) = 2×10^1 + 3×10^0 = 2×10 + 3×1 = 23

阶乘数3210所代表的数量的计算方法为

F(3210) = 3×3! + 2×2! + 1×1! + 0×0! = 3×6 + 2×2 + 1×1 + 1×0 = 23

对于阶乘数而言，由于阶乘的增长速度非常快，所以其可以表示的数值的范围随着位数的增长十分迅速，对于n位的阶乘数而言，其表示的范围从0～(n+1)!-1，总共(n+1)!个数。阶乘数有很多性质这里我们只介绍其和全排列相关的一些性质。

首先是加法操作，与普通十进制数的加法基本一样，所不同的是对于第n位F[n](最低位从第0位开始)，如果F[n]+1>n，那么我们需要将F[n]置0，同时令F[n+1]+1，如果对于第n+1位，也导致进位，则向高位依次执行进位操作。这里我们看一下F(3210)+1，对于第0位，有F[0]+1=0+1=1>0，所以F[0]=0（实际上阶乘数的第0位一直是0），F[1]+1=1+1=2>1，F[1]=0，……，依次执行，各位都发生进位，最终结果F(3210)+1=F(10000)。

其次，对于n位的阶乘数，每一个阶乘数的各位的数值，正好对应了一个n排列各位的逆序关系。这里以abcd为例。例如F(2110)，其对应的排列的意思是，对于排列的第一个元素，其后有两个元素比他小；第二个元素，后面有一个元素比他小；第三个元素，后面有一个元素比他小。最终根据F(2110)构建的排列为cbda。4位的阶乘数，与4排列的对应关系如下表所示。

0000	abcd	1000	bacd	2000	cabd	3000	dabc
0010	abdc	1010	badc	2010	cadb	3010	dacb
0100	acbd	1100	bcad	2100	cbad	3100	dbac
0110	acdb	1110	bcda	2110	cbda	3110	dbca
0200	adbc	1200	bdac	2200	cdab	3200	dcab
0210	adcb	1210	bdca	2210	cdba	3210	dcba

 

由此，我们就可以利用阶乘数与排列的对应关系构建集合的全排列，算法如下。

• 对于n个元素的全排列，首先生成n位的阶乘数F[0...n-1]，并令F[0...n-1]=0。
• 每次对F[0...n-1]执行+1操作，所得结果，根据其与排列的逆序对应关系，生成排列。
• 直到到达F[0...n-1]所能表示的最大数量n!-1为止，全部n!个排列生成完毕。

这里有一个问题需要解决，就是如何根据阶乘数，及其与排列逆序的对应关系生成对应的排列，这里给出一个方法，

• 以字典序最小的排列a[0...n-1]作为起始，令i从0到n-2。
• 如果F[i]=0，递增i。
• 否则令t=a[i+F[i]]，同时将a[i...i+F[i]-1]区间的元素，向后移动一位，然后令a[i]=t，递增i。

下面说明一下如何根据阶乘数F(2110)和初始排列abcd，构建对应的排列。首先，我们发现F[0]=2，所以我们要将a[0+2]位置的元素c放在a[0]位置，之前，先用临时变量t记录a[2]的值，然后将a[0...0+2-1]区间内的元素向后移动一位，然后令a[0]=t，得到cabd，i值增加1；然后有F[1]=1，所以我们要将a[1+1]=a[2]=b放在a[1]位置，同时将a[1]向后移动一位，得到排列cbad；然后有F[2]=1，所以将a[2+1]=a[3]=d放在a[2]位置，同时a[2]向后移动一位。最终得到cbda，排列生成结束。整个算法代码如下

 

 

inline int FacNumNext(unsigned int* facnum, size_t array_size)
{
    unsigned int i = 0;

    while(i < array_size)
    {
        if(facnum[i] + 1 <= i)
        {
            facnum[i] += 1;
            return 0;
        }
        else
        {
            facnum[i] = 0;
            ++i;
        }
    }

    return 1;
}

/*
 * 根据阶乘数所指定的逆序数根据原始字符串构建排列输出
 */
inline void BuildPerm(const char* array, size_t array_size, const unsigned int* facnum, char* out)
{
    char t;
    unsigned int i, j;

    memcpy(out, array, array_size * sizeof(char));

    for(i = 0; i < array_size - 1; ++i)
    {
        j = facnum[array_size - 1 - i];

        if(j != 0)
        {
            t = out[i + j];
            memmove(out + i + 1, out + i, j * sizeof(char));
            out[i] = t;
        }
    }
}

/*
 * 基于阶乘数（逆序数）的全排列生成算法
 */
void FullArray(char* array, size_t array_size)
{
    unsigned int facnum[array_size];
    char out[array_size];

    for(unsigned int i = 0; i < array_size; ++i)
    {
        facnum[i] = 0;
    }

    BuildPerm(array, array_size, facnum, out);

    for(unsigned int i = 0; i < array_size; ++i)
    {
        cout << out[i] << ' ';
    }

    cout << '\n';

    while(!FacNumNext(facnum, array_size))
    {
        BuildPerm(array, array_size, facnum, out);

        for(unsigned int i = 0; i < array_size; ++i)
        {
            cout << out[i] << ' ';
        }

        cout << '\n';
    }
}

 

 

用该算法生成1234全排列，顺序如下图，该图来自与Wiki百科。

从生成排列顺序的角度讲，概算法相较于字典序和最小变更有明显优势，但是在实际应用中，由于根据阶乘数所定义的逆序构建排列是一个O(n^2)时间复杂度的过程，所以算法的整体执行效率逊色不少。但是通过阶乘数建立逆序数与排列对应关系的思路，还是十分精彩的，值得借鉴

 

 

转载于:https://www.cnblogs.com/cswangchen/p/7469645.html