生成式对抗网络（GAN）

 　　生成对抗网络（GAN），是深度学习模型之一，2014年lan Goodfellow的开篇之作Generative Adversarial Network，

GAN概述

　　GAN包括两个模型，一个是生成模型（generative model），一个是判别模型（discriminative model）。生成模型要做的事情就是生成看起来真的和原始数据相似的实例，判断模型就是判断给定的实例是生成的还是真实的（真实实例来源于数据集，伪造实例来源于生成模型）。

　　生成器试图欺骗判别器，判别器则努力不被生成器欺骗。两个模型经过交替优化训练，互相提升

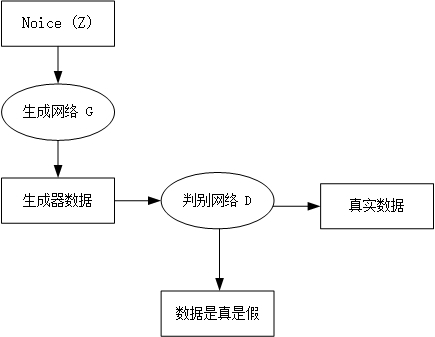
图1-1   GAN网络整体示意图

　　如上图所示，我们有两个网络，生成网络G（Generayor）和判别网络D（Discriminator）。生成网络接收一个（符合简单分布如高斯分布或者均匀分布的）随机噪声输入，通过这个噪声输出图片，记做G(z)。判别网络的输入是x，x代表一张图片，输出D(x)代表x为真实图片的概率。

GAN模型优化训练

目的：将一个随机高斯噪声z通过一个生成网络G得到一个和真实数据分布\({p_{data}}(x)\)差不多的生成数据分布\({p_G}(x;\theta )\)，其中的参数\(\theta \)是网络参数决定的，我们希望找到\(\theta \)使得\({p_G}(x;\theta )\)和\({p_{data}}(x)\)尽可能的接近。

我们站在判别网络的角度想问题，首先判别器要能识别真实数据，同样也能识别出生成数据，在数学式子上的表达为D(x)=1和D(G(z))=0。我们通过这两个式子，分别来构造[正类](判别出x属于真实数据)和[负类](判别出G(z)属于生成数据)的对数损失函数。

生成网络G的损失函数为\(\log (1 - D(G(z)))\)或者\( - \log D(G(z))\)。

判别网络D的损失函数为\( - (\log D(x) + \log (1 - D(G(z))))\)。

　　我们从式子中解释对抗，损失函数的图像是一个类似于y=log(x)函数图形，x<0时,y>0,x=1时,y=0，生成网络和判别网络对抗（训练）的目的是使得各自的损失函数最小，，生成网络G的训练希望\(D(G(z))\)趋近于1，也就是正类，这样生成网络G的损失函数\(\log (1 - D(G(z)))\)就会最小。而判别网络的训练就是一个2分类，目的是让真实数据x的判别概率D趋近于1，而生成数据G(z)的判别概率\(D(G(z))\)趋近于0，这是负类。

当判别网络遇到真实数据时：\({E_{x \sim {p_{data}}(x)}}[\log D(x)]\)，这个期望要取最大，只有当D(x)=1的时候，也就是判别网络判别出真实数据是真的。

当判别网络遇到生成数据时：\({E_{z \sim Pz(z)}}[\log (1 - D(G(z)))]\)，因为0<概率<1，且x<1的对数为负，这个数学期望要想取最大值，则需要令D(G(z))=0，D(G(z))=0是判别器发现了生成数据G(z)是假的，

　　结合以上两个概念，判别网络最大化目标函数为：\[{E_{x \sim {p_{data}}(x)}}[\log D(x)] + {E_{z \sim Pz(z)}}[\log (1 - D(G(z)))]\]

　　以上的式子，是在给定生成器G，求最优的判别器\(D_G^*\)，即判别网络的最大值，我们定义一个价值函数，如下\[V(G,D) = {E_{x \sim {p_{data}}(x)}}[\log D(x)] + {E_{z \sim Pz(z)}}[\log (1 - D(G(z)))]\]

　　然后我们将最优化式子表述为：\(D_G^* = \arg {\max _D}V(G,D)\)

　　现在剧情大反转，对于判别网络D而言，希望目标函数(判别公式\(V(D,G)\))最大化，但对于生成网络G，希望目标函数（判别公式\(V(D,G)\)）最小化，即你判别网络判别不出我是真数据还是生成数据。有趣的事情来了，那到底是希望这个目标函数最大化好呢，还是最小化好呢？来打一架吧。整个训练的过程是一个迭代的过程，其实

　　当我们求得最优的\(D_G^*\)即\(D = D_G^*\)，我们反过来把\(D = D_G^*\)代入上面的式子，来求最优(最小)的G，即\(G_D^*\)。整个训练优化过程就是一个循环迭代过程。在原论文中lan J.Goodfellow更喜欢求解最优化价值函数的G和D以求解极大极小博弈：

\[\mathop {\min }\limits_G \mathop {\max }\limits_D V(D,G) = {E_{x \sim {p_{data}}(x)}}[\log D(x)] + {E_{z \sim Pz(z)}}[\log (1 - D(G(z)))]\]

式中：D是判别函数，x是真实数据，D(x)：判别真实数据的概率，D(G(z))：判别生成数据的概率

　　最后我们将最优化问题表达为：\[G_D^* = \arg {\max _G}V(G,D_G^*)\]

　　其实极小极大博弈可以分开理解，即在给定G的情况下先最大化V(D,G)而取\(D_G^*\)，然后固定D，并最小化V(D,G)而得到\(G_D^*\)。其中给定G，最大化V(D,G)评估了真实数据和生成数据之间的差异或距离。

　　在这样的对抗过程中，会有几个过程，原论文中的图如下：

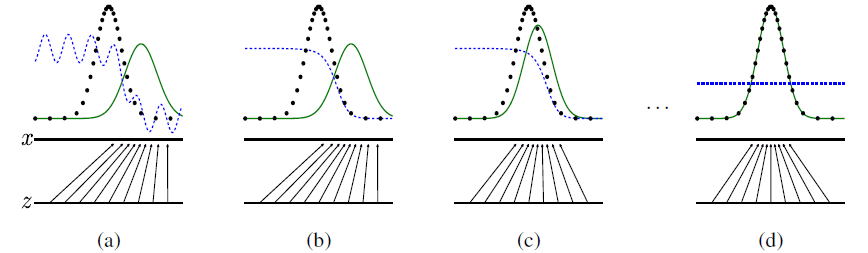
黑色线表示真实数据的分布，绿色线表示生成数据的分布，蓝色线表示生成数据在判别器中的分布效果

 我们对每个图逐一进行分析

（a）、判别网络D还未经过训练，分类能力有限，有波动，但是真实数据x和生成数据G(z)还是可以的

（b）、判别网络D训练的比较好，可以明显区分出生成数据G(z)。

（c）、绿色的线与黑色的线偏移了，蓝色线下降了，也就是判别生成数据的概率下降了。

　　由于绿色线的目标是提升提升概率，因此会往蓝色线高的方向引动。那么随着训练的持续，由于G网络的提升，生成网络G也反过来影响判别网络D的分布。在不断循环训练判别网络D的过程中，判别网络的判别能力会趋于一个收敛值，从而达到最优。\[D_G^*(x) = \frac{{{p_{data}}(x)}}{{{p_{data}}(x) + {p_g}(x)}}\]

　　因此随着\({{p_g}(x)}\)趋近于\({{p_{data}}(x)}\)，\(D_G^*(x)\)会趋近于\(\frac{1}{2}\)，\(\frac{1}{2}\)的意思就是模棱两可，判别器已经分不清随是真实数据谁是生成数据，也就是图d。

 以上只是图文说明\({{p_g}(x)}\)最终会收敛于\({{p_{data}}(x)}\)，接下来我们用算法具体推理。

GAN的算法推导

KL散度

　　在信息论中，我们使用香农熵（Shannon entropy）来对整个概率分布中的不确定性总量进行量化：\[H(x) = {E_{x \sim p}}[I(x)] =  - {E_{x \sim p}}[\log P(x)]\]

　　首先需要一点预备知识，如果我们对于同一个随机变量x有两个单独的概率分布P(x)和Q(x)，我们可以使用KL散度（Kullback-Leibler divergence）也称为相对熵，这是统计中的一个概念，是衡量两种概率分布的相似程度，其越小，表示两种概率分布越接近。

对于离散数据的概率分布，定义如下：\[{D_{KL}}(P\parallel Q) = \sum\limits_x {P(x)\log \frac{{P(x)}}{{Q(x)}}}  = {E_{x \sim P}}[\log \frac{{P({\rm{x}})}}{{Q(x)}}] = {E_{x \sim P}}[\log P(x) - \log Q(x)]\]

对于连续数据的概率分布，定义如下：\[{D_{KL}}(P||Q) = \smallint _{ - \infty }^\infty p(x)log\frac{{p(x)}}{{q(x)}}dx\]

　　在离散变量的情况下，KL散度衡量的是：我们使用一种编码，使得概率分布Q产生的消息长度最短。再用这种编码，发送包含由概率分布P产生的符号的消息时，所需要的额外信息量。

KL散度的性质：

1、最重要的是他是非负的。

2、当前仅当P和Q在离散型变量的情况下是相同分布，或者P和Q在连续型变量的情况下是几乎处处相等，那么KL散度为0。

3、因为 KL 散度是非负的并且衡量的是两个分布之间的差异，它经常 被用作分布之间的某种距离。然而，它并不是真的距离因为它不是对称的：对于某些 P 和 Q，\({D_{KL}}(P\parallel Q)\)不等于\({D_{KL}}(Q\parallel P)\)。这种非对称性意味着选择\({D_{KL}}(P\parallel Q)\)还是\({D_{KL}}(Q\parallel P)\)影响很大。

推导KL散度

　　在李宏毅的讲解中，KL散度可以从极大拟然估计中推导而出。若给定一个真实数据的分布\({P_{data}}(x)\)和生成数据的分布\({P_G}(x;\theta )\)，那么GAN希望能够找到一组参数\(\theta \)使得真实数据的分布\({P_{data}}(x)\)和生成数据的分布\({P_G}(x;\theta )\)之间距离最短，也就是找到一组生成器参数使得生成器能够生成十分逼真的图片。

　　我们从真实数据分布\({P_{data}}(x)\)里面取样m个点，\({x^1},{x^2}, \cdots ,{x^m}\)，根据给定的参数\(\theta \)我们可以计算生成分布中第i个样本\({x^i}\)出现的概率\({P_G}({x^i};\theta )\)，那么生成这m个样本数据的拟然函数就是

\[L = \mathop \Pi \limits_{i = 1}^m {P_G}({x^i};\theta )\]

L为全部真实样本在生成分布中出现的概率。又因为若 P_G(x;θ) 分布和 P_data(x) 分布相似，那么真实数据很可能就会出现在 P_G(x;θ) 分布中，因此 m 个样本都出现在 P_G(x;θ) 分布中的概率就会十分大。

下面我们可以最大化拟然函数L来求得离真实分布最近的生成分布（即找到最优的参数\({\theta ^*}\)）：

\[{\theta ^*} = \mathop {\arg \max }\limits_\theta  \mathop \Pi \limits_{i = 1}^m {p_G}({x^i};\theta ) \Leftrightarrow \mathop {\arg \max }\limits_\theta  \log \mathop \Pi \limits_{i = 1}^m {P_G}({x^i};\theta )\]

\[ = \mathop {\arg \max }\limits_\theta  \sum\limits_{i = 1}^m {\log } {P_G}({x^i};\theta )\left\{ {{x^1},{x^2}, \cdots ,{x^m}} \right\}from{P_{data}}(x)\]

\[ \approx \mathop {\arg \max }\limits_\theta  {E_{x \sim {P_{data}}}}[\log {P_G}(x;\theta )]\]

\[ \Leftrightarrow \mathop {\arg \max }\limits_\theta  \int_x {{P_{data}}} (x)\log {P_G}(x;\theta )dx - \int_x {{P_{data}}} (x)\log {P_{data}}(x)dx\]

\[ = \mathop {\arg \max }\limits_\theta  \int_x {{P_{data}}} (x)\log \frac{{{P_G}(x;\theta )}}{{{P_{data}}(x)}}dx\]

\[ = \mathop {\arg \min }\limits_\theta  KL({P_{data}}(x)||{P_G}(x;\theta ))\]

分析推导过程：

1、我们希望得到最大化拟然函数L，简化求解过程，对拟然函数取对数，那么累乘就转换成累加，并且这一过程并不会改变最优结果。因此我们可以将极大似然估计化为求令\(\log {P_G}(x;\theta )\)期望最大化的\(\theta \)

2、期望\({E_{x \sim \;{P_{data}}}}[\log {P_G}(x;\theta )]\)可以展开为\(\int_x {{P_{data}}} (x)\log {P_G}(x;\theta )dx\)在 x 上的积分形式。

3、因为该最优化过程是针对 θ 的，所以我们多减去一项\(\int_x {{P_{data}}} (x)\log {P_{data}}(x)dx\)，不含 θ的积分并不影响优化效果，因为这相当于是一个参数。

4、合并这两个积分并构造类似KL散度的形式

上面的积分就是KL散度的积分形式，所以我们想要求得生成分布和真实分布尽可能靠近的参数θ，那么我们只需要求令KL散度最小化的参数θ（最优的θ）。

这里在前面添加一个负号，将log里面的分数倒一下，就变成了KL散度（KL divergence）

但是\({P_G}(x;\theta )\)如何算出来呢？

\[{P_G}(x) = \int_z {{P_{prior}}} (z){I_{[G(z) = x]}}dz\]

里面的I表示示性函数，也就是

\[{I_{G(z) = x}} = \left\{ {\begin{array}{*{20}{l}}0&{G(z) \ne x}\\1&{G(z) = x}\end{array}} \right.\]

这样我们其实根本没办法求出这个\({P_G}(x)\)出来，这就是生成模型的基本想法。

其他人推导存在的问题

Scott Rome对原论文的推导有这么一个观念，他认为原论文忽略了可逆条件，原论文的推理过程不够完美。我们开看看到底哪里不完美：

在GAN原论文中，有一个思想和其他方法不同，即生成器G不需要满足可逆条件，即G不可逆

scott Rome认为：在实践过程中G就是不可逆的。

其他人：证明时使用积分换元公式，，而积分换元公式恰恰是基于G的可逆条件。

Scott认为证明只能基于以下等式成立：

\[{E_{z \sim Pz(z)}}[\log (1 - D(G(z)))] = {E_{x \sim {P_G}(x)}}[\log (1 - D(x)]\]

该等式来源于测度论中的 Radon-Nikodym 定理，它展示在原论文的命题 1 中，并且表达为以下等式：

\[\int\limits_x {{p_{data}}(x)} \log D(x)dx + \int\limits_z {p(z)} \log (1 - D(G(z)))dz\]

\[ = \int\limits_x {{p_{data}}(x)} \log D(x)dx + {p_G}(x)\log (1 - D(x))dx\]

我们这里使用了积分换元公式，但进行积分换元就必须计算 G^(-1)，而 G 的逆却并没有假定为存在。并且在神经网络的实践中，它也并不存在。可能这个方法在机器学习和统计学文献中太常见了，因此很多人忽略了它。

　　满足Radon-Nikodym 定理条件之后。我们利用积分换元变换一下之前定义的目标函数：

\[\mathop {\min }\limits_G \mathop {\max }\limits_D V(D,G) = {E_{x \sim {p_{data}}(x)}}[\log D(x)] + {E_{x \sim PG}}[\log (1 - D(x))]\]

　　然后通过下面的式子求最优的生成网络模型\[{G^*} = \arg \mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D)\]

最优判别器

　　首先我们只考虑\(\mathop {\max }\limits_D V(G,D)\)，在给定G的情况下，求一个合适的D使得V(G,D)取得最大。这是一个简单的微积分。

\[\begin{array}{l}V = Ex \sim {P_{data}}[logD(X)] + Ex \sim {P_G}[log(1 - D(x))]\\ = \mathop \smallint \limits_x {P_{data}}(x)\log D(x)dx + \mathop \smallint \limits_x {p_G}(x)\log (1 - D(x))dx\\ = \int_x {[{P_{data}}(x)logD(X)] + {P_G}(x)log(1 - D(x))]dx} \end{array}\]

　　对于这个积分，要取其最大值，只要被积函数是最大的，就能求到最大值，我们称之为最优的判别器\({D^*}\)\[{D^*} = {P_{data}}(x)\log D(x) + {P_G}(x)\log (1 - D(x))\]

　　在真实数据给定和生成数据给定的前提下，\({P_{data}}(x)\)和\({P_G}(x)\)都可以看做是常数，我们用a、b来表示他们，如此一来得到下面的式子：\[\begin{array}{*{20}{l}}{f(D) = a\log (D) + b\log (1 - D)}\\{\frac{{df(D)}}{{dD}} = a*\frac{1}{D} + b*\frac{1}{{{\rm{1}} - {\rm{D}}}}*( - 1) = 0}\\{a*\frac{1}{{{D^*}}} = b*\frac{1}{{1 - {D^*}}}}\\{ \Leftrightarrow a*(1 - {D^*}) = b*{D^{\rm{*}}}}\\{ \Leftrightarrow {D^{\rm{*}}}(x) = \frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}(while{P_{data}}(x) + {P_G}(x) \ne 0)}\end{array}\]

如果我们继续对f(D)求二阶导，并把极值点\({{D^{\rm{*}}}(x) = \frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}}\)代入：

\[\frac{{df{{(D)}^2}}}{{{d^2}D}} =  - \frac{{{P_{data}}(x)}}{{{{(\frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_{\rm{G}}}(x)}})}^2}}} - \frac{{{P_{\rm{G}}}(x)}}{{1 - {{(\frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_{\rm{G}}}(x)}})}^2}}} < 0\]

　　其中0<a,b<1，因为一接到等于0、二阶导小于0，所以\({\frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}}\)为极大值，\({{D^{\rm{*}}}(x)}\)即为最优判别器。

　　这样我们就求得了在真实数据给定和生成数据给定的前提下，能够使得V(D)取得最大值的D，其实该最优的 D 在实践中并不是可计算的，但在数学上十分重要。我们并不知道先验的 P_data(x)，所以我们在训练中永远不会用到它。另一方面，它的存在令我们可以证明最优的 G 是存在的，并且在训练中我们只需要逼近 D。

最优生成器

当前仅当\({P_G}(x) = {P_{data}}(x)\)时，意味着\[D_G^* = \frac{{{P_{data}}(x)}}{{{P_G}(x) + {P_{data}}(x)}} = \frac{1}{2}\]

判别器已经分不清谁是真实数据谁是生成数据了，我们代入目标函数V(G,D)，即进入极大极小博弈仪式的第二步，求令\(V(G,{D^*})\)最小的生成器\({G^*}\)(最优生成器)。

原论文中的这一定理是「当且仅当」声明，所以我们需要从两个方向证明。首先我们先从反向逼近并证明V(G,D)的取值，然后再利用由反向获得的新知识从正向证明。设\({P_G}(x) = {P_{data}}(x)\)（反向指预先知道最优条件并做推导），我们可以反向推出：

\[V(G,D_G^*) = \int_x {{P_{data}}(x)log\frac{1}{2}] + {P_G}(x)log(1 - \frac{1}{2})dx} \]

\[ \Leftrightarrow V(G,D_G^*) =  - \log 2\int\limits_x {{P_G}(x)} dx - \log 2\int\limits_x {{P_{data}}(x)} dx =  - 2\log 2 =  - \log 4\]

该值是全局最小值的候选，因为它只有在\({P_G}(x) = {P_{data}}(x)\)的时候才出现。我们现在需要从正向证明这一个值常常为最小值，也就是同时满足「当」和「仅当」的条件。现在放弃\({P_G}(x) = {P_{data}}(x)\)的假设，对任意一个 G，我们可以将上一步求出的最优判别器 D* 代入到V(G,D) 中，得到如下的结果\[{\max V(G,D) = V(G,{D^*})}\]

\[{ = {E_{x \sim {p_{data}}(x)}}[\log \frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}] + {E_{x \sim PG}}[\log \frac{{{P_G}(x)}}{{{P_{data}}(x) + {P_G}(x)}}]}\]

\[{ = \int\limits_x {{P_{data}}(x)\log \frac{{\frac{1}{2}{P_{data}}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}}dx}  + \int\limits_x {{P_G}(x)\log \frac{{\frac{1}{2}{P_G}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}}dx} }\]

\[ = \int\limits_x {{P_{data}}(x)( - \log 2 + \log \frac{{{P_{data}}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}})}  + {P_G}(x)( - \log 2 + \log \frac{{{P_G}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}})dx\]

\[ =  - \log 2\int\limits_x {{P_{data}}(x) + } {P_G}(x)dx + \int\limits_x {{P_{data}}(x)(\log \frac{{{P_{data}}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}})} dx + \int\limits_x {{P_G}(x)(\log \frac{{{P_G}(x)}}{{\frac{{{P_{data}}(x) + {P_G}(x)}}{2}}})dx} \]

因为概率密度的定义，\({{P_{data}}(x)}\)和\({P_G}(x)\)在它们积分域上的积分等于1，结合之前介绍的KL散度，推理出下式：

\[{ =  - 2log2 + KL({P_{data}}(x)||\frac{{{P_{data}}(x) + {P_G}(x)}}{2}) + KL({P_G}(x)||\frac{{{P_{data}}(x) + {P_G}(x)}}{2})}\]

KL 散度是非负的，所以我们马上就能看出来 -log4 为V(G,D)的全局最小值。

　　之所以当 P_G(x)=P_data(x) 可以令价值函数最小化，是因为这时候两个分布的 JS 散度 [JSD(P_data(x) || P_G(x))] 等于零，看到这里我们其实就已经推导出了为什么这么衡量是有意义的，因为我们取D使得V(G,D)取得min值，这个时候这个min值是由两个KL divergence构成的，相当于这个min的值就是衡量\({P_G}(x)\)与\({P_{data}}(x)\)的差异程度就能够取到G使得这两种分布的差异最小，这样自然就能够生成一个和原分布尽可能接近得分布。

　　还没有结束，哇！证明好累呀，快结束了那就再坚持一下吧。

　　我们还要进一步证明有且仅有一个G能够达到这个最小值。

我们来介绍一下JS散度，

\[JSD(P\parallel Q) = \frac{1}{2}[D(P\parallel M) + D(Q\parallel M)]\]

\[M = \frac{1}{2}(P + Q)\]

假设存在两个分布 P 和 Q，且这两个分布的平均分布 M=(P+Q)/2，那么这两个分布之间的 JS 散度为 P 与 M 之间的 KL 散度加上 Q 与 M 之间的 KL 散度再除以 2。这里P为\({P_{data}}(x)\)，Q为\({P_G}(x)\)。

JS 散度的取值为 0 到 log2。若两个分布完全没有交集，那么 JS 散度取最大值 log2；若两个分布完全一样，那么 JS 散度取最小值 0。

因此V(G,D)可以根据JS散度的定义改写为：\[V(G,D) =  - \log 4 + 2*JSD({P_{data}}(x)|{P_G}(x))\]

这一散度其实就是Jenson-Shannon距离度量的平方。根据他的属性：当\({P_G}(x) = {P_{data}}(x)\)时，\(JSD({P_{data}}(x)|{P_G}(x))\)为0。综上所述，生成分布当前仅当等于真实数据分布式时，我们可以取得最优生成器。

原论文还有额外的证明白表示：给定足够的训练数据和正确的环境，训练过程将收敛到最优 G，我们并不详细讨论这一块。

实现

 

 

 

GAN的优缺点

 

参考资料：

这篇博客以下内容我以后再完善

知乎GAN数学推导

机器之心：GAN推理与实现

Scott Rome GAN 推导：http://srome.github.io//An-Annotated-Proof-of-Generative-Adversarial-Networks-with-Implementation-Notes/

Goodfellow NIPS 2016 Tutorial：https://arxiv.org/abs/1701.00160

李弘毅MLDS17：http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html

转载于:https://www.cnblogs.com/LXP-Never/p/9706790.html